神经场 (Neural Fields) 是当今机器学习领域最令人振奋的发展之一。你很可能已经见过它们最著名的应用——神经辐射场 (NeRFs) , 它只需少量二维图像就能生成令人惊叹、逼真的三维场景。从本质上看, 神经场 (NFs) 简单而强大: 它们使用神经网络将输入坐标 (如图像中的 \((x, y)\) 或三维场景中的 \((x, y, z)\)) 映射到输出值 (如 RGB 颜色或密度) 。这种优雅的方式能够在图像、音频、视频或三维空间等多种模态中以惊人的紧凑性实现连续数据表示。

然而，这种方法面临两大挑战:

  1. 训练速度: 从零开始为一个场景拟合一个神经场可能需要数小时甚至数天。
  2. 灾难性遗忘: 当模型在新数据上重新训练时，神经网络往往会覆盖先前的知识。

想象一架无人机逐块绘制城市地图，或一颗卫星在不同时间拍摄同一区域。模型必须能够顺序学习 , 不遗忘过去的信息，并且能快速适应新数据。

首尔大学最近的一篇论文—— 《神经场的元持续学习 (MCL-NF) 》 ——正面解决了这一挑战。它提出了一个新的问题设定和一个框架，将元学习的适应性与持续学习的稳定性结合起来。让我们来看看它是如何工作的。

理解基础

要理解 MCL-NF 的创新，我们首先回顾三个基本支柱: 神经场 (NF) 、持续学习 (CL) 和元学习 (ML) 。

神经场 (NF)

神经场是一个由神经网络 \(f_{\theta}\) 参数化的函数，它将坐标 \(x\) 映射到值 \(y\)。

  • 对于二维图像: \(x = (x, y)\) → \(y = (R, G, B)\)。
  • 对于三维 NeRF: \(x = (x, y, z, \theta, \phi)\) → \(y = (\text{color}, \text{density})\)。

所有场景信息都被编码在参数 \(\theta\) 中，使神经场内存占用高效，但训练速度较慢。

持续学习 (CL)

持续学习研究的是在一系列任务 \(\mathcal{T}_1, \mathcal{T}_2, \ldots, \mathcal{T}_n\) 上训练模型的能力，其中过去的数据不一定可访问。目标是在保留过往学习成果的同时获取新知识。

常见的持续学习策略包括:

  • 基于回放的方法: 在训练过程中保存并重访过去样本。
  • 基于正则化的方法: 限制对旧任务关键参数的改动。
  • 模块化方法: 为不同任务分配网络的不同模块，避免相互干扰。

元学习 (ML)

元学习，又称“学会学习”，关注快速适应。最常用的算法——模型无关元学习 (MAML) ——通过学习一个有效的初始化参数 \(\theta_0\)，使新任务只需少量梯度更新即可快速收敛。MAML 并不防止遗忘，而是优化快速学习能力。

MCL-NF 旨在结合元学习的速度与持续学习的记忆保持能力 , 构建一个既学得快又记得牢的模型。

核心创新: MCL-NF 的三大支柱

MCL-NF 框架结合了三项关键设计: (1) 带有共享初始化的模块化架构，(2) 新颖的基于费雪信息的损失函数，(3) 稳定性与收敛性的理论保证。

1. 带有共享元学习初始化的模块化

架构是模块化的: 每个任务分配独立模块，而非一个单一大型网络。 例如:

  • 在视频任务中: 每一帧或一组帧作为一个任务模块。
  • 在大型 NeRF 模型中: 每个城市街区作为一个独立模块。

这种结构通过将参数隔离避免灾难性遗忘。但关键洞察在于通过 MAML 实现的共享初始化 。

在元训练阶段，系统学习一个通用的初始化参数 \(\theta_{\text{shared}}\)。 在元测试阶段，每个新模块从 \(\theta_{\text{shared}}\) 开始，并微调到自身任务。

这种设计结合了:

  • 隔离性 (模块记住各自任务) ；
  • 速度 (所有模块从优化的初始化状态出发) 。

结果是快速收敛与持久记忆。

2. FIM-Loss: 优先学习高信息量样本

即使模块化模型也可能存在冗余。例如，两个相邻城市街区可能共享类似视觉模式。为提高学习效率，模型应关注那些对参数更新贡献最大的高信息量样本 。

第二项创新引入了费雪信息最大化损失 (FIM-Loss) ——一种对标准均方误差 (MSE) 的加权改进版本。

标准的 MAML 最小化基于 MSE 的目标函数:

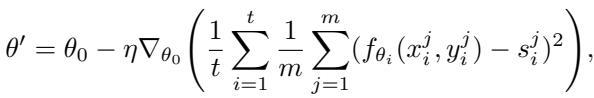
标准的 MAML 目标函数，旨在最小化一系列任务的均方误差。

图: 标准的 MAML 目标函数在任务间最小化均方误差。

作者在此基础上加入了样本特定权重 \(w_{ij}\):

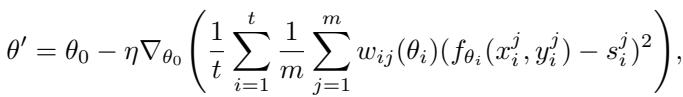
提出的 FIM-Loss，在标准 MSE 损失的基础上增加了一个权重项 w_ij。

图: FIM-Loss 引入了源自费雪信息的样本加权项。

权重 \(w_{ij}\) 由费雪信息矩阵 (FIM) 计算，该矩阵衡量一个样本对模型参数优化所提供的信息量:

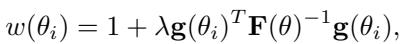
FIM-Loss 权重的计算公式，其值取决于超参数 λ、梯度向量 g 和费雪信息矩阵的逆矩阵 F。

图: 权重项依赖于超参数 \(\lambda\)、梯度向量 \(\mathbf{g}\) 以及费雪信息矩阵的逆矩阵。

原理如下:

  • \(\mathbf{g}(\theta_i)\): 样本对数似然的梯度，代表敏感度或“意外程度”；
  • \(\mathbf{F}(\theta)^{-1}\): 费雪矩阵逆，用于归一化参数重要性；
  • \(\lambda\): 控制费雪信息的作用强度。

通过聚焦高信息样本，模型能在关键区域“更用功地学习”，实现更快收敛与更好泛化。

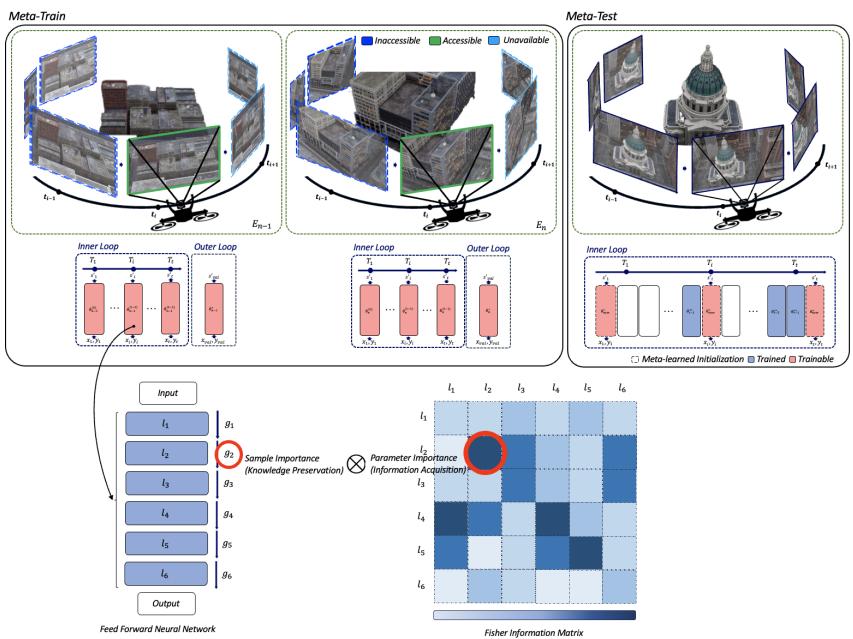
从传统 MSE 损失到 FIM-Loss 的过渡示意图。图中展示了如何使用 FIM 计算样本权重，这些权重随后被整合到最终损失中，使模型优先学习信息丰富的样本。

图: 从传统 MSE 损失到 FIM-Loss 的演变展示了样本权重如何引导学习聚焦信息密集区域。

与以往基于费雪信息的方法 (如弹性权重巩固 (EWC) , 在参数层面保持旧知识) 不同, FIM-Loss 在样本层面发挥作用，动态提升学习效率与适应性。

3. 理论保证

为在数学上验证该方法的合理性，作者证明 FIM-Loss 与信息增益最大化之间存在联系。

他们指出，费雪信息提供了参数分布间 KL 散度 的局部近似:

\[ KL[p(\mathcal{D}|\theta)||p(\mathcal{D}|\theta + \Delta\theta)] \approx \frac{1}{2} \Delta \theta^{T} \mathbf{F}(\theta) \Delta \theta \]

这说明，用 FIM 优化隐含地在最大化参数与数据间的互信息 , 从而提升泛化能力并保持收敛稳定。 他们的理论分析还为FIM 增强的随机梯度下降 (FIM-SGD) 提供了收敛与泛化界限，证明 MCL-NF 既实用又有理论可靠性。

实验: 跨模态学习

研究人员在多种任务和数据集上测试了 MCL-NF:

  • 图像重建: CelebA、FFHQ、ImageNette
  • 视频重建: VoxCeleb2
  • 音频重建: LibriSpeech
  • 视图合成 (NeRF) : MatrixCity

他们对比了自研方法—— “Ours (mod)” (模块化) 与 “Ours (MIM)” (模块化 + FIM-Loss) ——与主流基线 ER、EWC、MAML+CL、OML。

快速适应与高保真度

重建质量通过 PSNR (值越高越好) 与测试优化步数的关系进行评估。

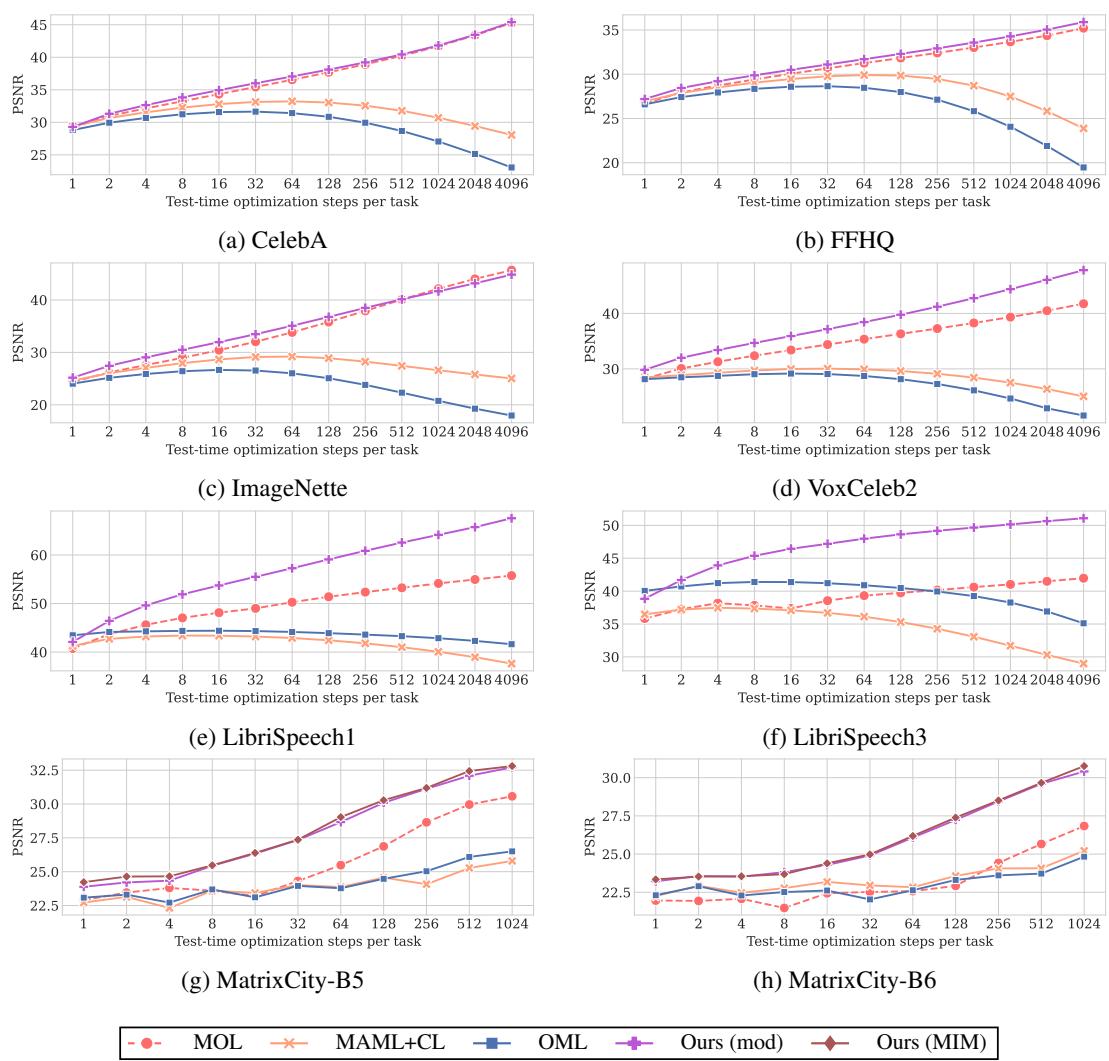
不同元学习方法在适应步骤中的 PSNR 比较。我们的方法显示，随着步骤数的增加，PSNR 持续改善，并在所有模态和数据集上优于传统 MAML 与 OML。

图 2: 不同方法在适应步骤中的 PSNR 对比。MCL-NF 功能持续提升且最终质量最佳。

在所有数据集中，所提方法以更少步数获得更高 PSNR。相比之下，MAML+CL 与 OML 提前进入平台期，而 MCL-NF 稳步提升，展现了快速收敛与长期稳定性——有效缓解灾难性遗忘。

大规模任务中的量化优势

跨模态性能比较证明了 MCL-NF 的领先效果。

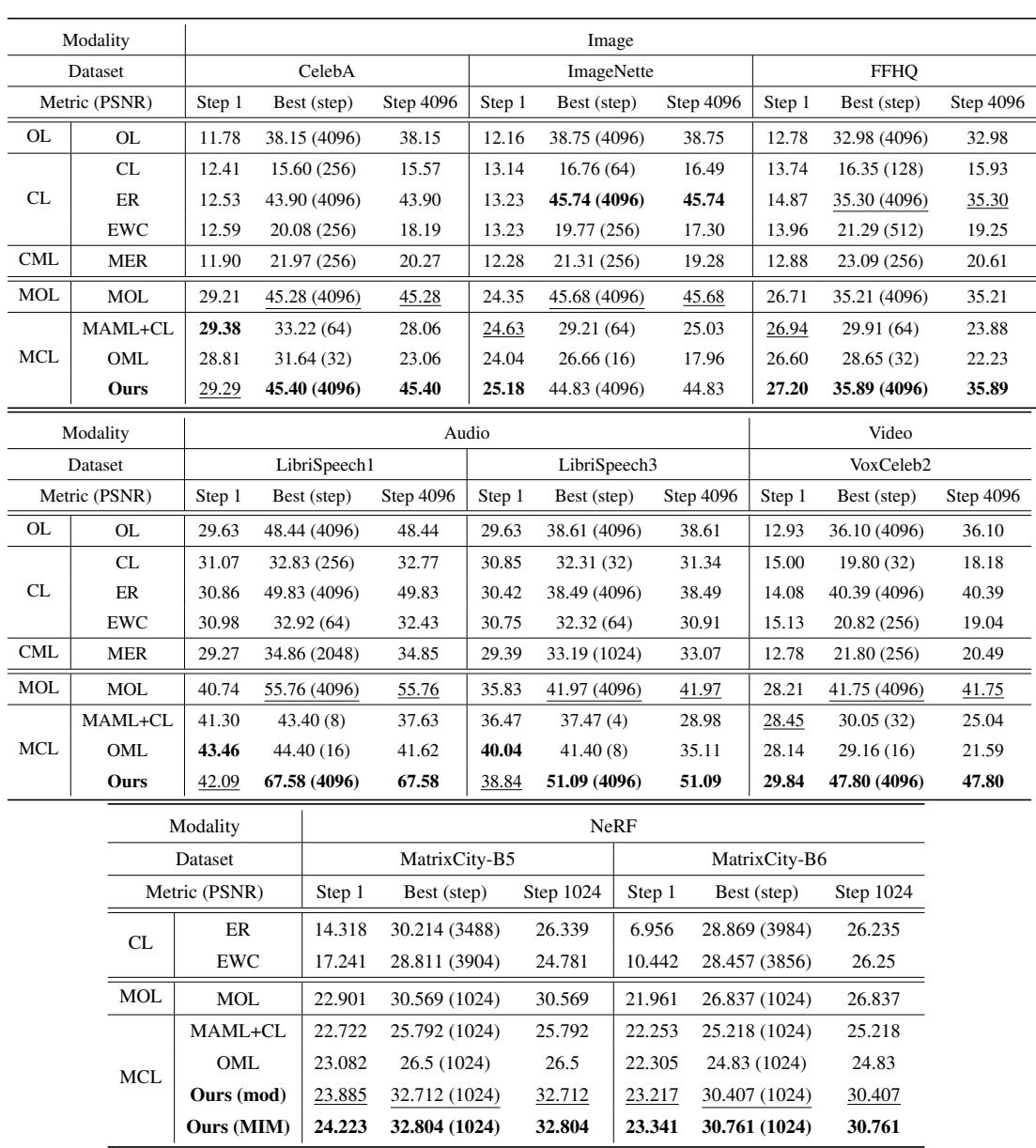
在三个关键时间点 (第 1 步的初始性能、最佳步和第 4096 步的最终性能) 下的 PSNR 对比。所提方法持续名列前茅。

图 3: 各方法与数据集的量化结果。MCL-NF 在整个训练过程中保持领先或接近最佳表现。

无论是在第 1 步、峰值步还是第 4096 步评估, MCL-NF 始终位居前列——展示了强大的初始化与稳健进步能力。

视觉质量: 眼见为实

定性结果凸显了视觉上的显著提升。

图像重建的定性结果。第一列为真实图像，其余列显示不同方法的重建结果。每张图片下方数字表示相对于真实图像的 PSNR。

图 4: CelebA、FFHQ、ImageNette 的视觉对比。“Ours” 始终生成更清晰、更干净的重建。

与基线方法相比，MCL-NF 生成的图像更清晰、无伪影，颜色再现准确，细节保真度高。

规模化: 城市级神经场

最令人印象深刻的实验是 MatrixCity , 一个城市级视图合成基准。为整座城市训练 NeRF 通常耗费庞大资源。通过模块划分 (任务分片) 和共享初始化，MCL-NF 高效实现大规模渲染，以更少参数保持高保真度。

“mod” 与 “mim” 方法的重建过程可视化。随着优化步数增加，重建细节逐渐提升，其中 “mim” 表现出更快的细节优化。

图 5: 城市级 NeRF 渲染重建过程。“MIM” 展示了更快、更清晰的细节优化。

连续的可视化结果显示，随着优化步数增加，细节逐渐锐化，最终生成清晰逼真的城市景观——显示出强大的可扩展性与鲁棒性。

结论与展望

神经场的元持续学习 (MCL-NF) 框架为资源受限场景下的持续快速学习提供了统一方案。通过结合:

  • 模块化架构保证记忆稳定；
  • 元学习共享初始化加速适应；
  • 基于信息论的 FIM-Loss 进行智能样本加权；

MCL-NF 成功克服灾难性遗忘，在图像、音频、视频与三维渲染任务中均展现卓越的学习效率。

这项研究为能即时学习的自适应系统铺平了道路——理想用于无人机、自主导航、环境监测与城市级实时建模。尽管随着模块增多可能带来额外内存开销，但此工作标志着迈向真正持续、可扩展神经场学习的重要一步。

简言之，MCL-NF 是在连接速度与稳定性之间迈出的关键一步——让神经场能够像它们要建模的动态世界一样，持续学习、记忆并不断进化。