引言

在高维统计学和机器学习的世界里，很少有问题像学习高斯混合模型 (Gaussian Mixture Models, GMMs) 那样经典而又棘手。我们几乎在所有领域都使用它们——从天体物理学到市场营销——来模拟由不同子群组成的群体。

GMM 的理论格局呈现出两个极端的态势。一方面，如果分量是球形的 (完美的圆形团块) ，我们可以高效地学习它们。另一方面，如果分量是任意的“煎饼” (高度压扁的高斯分布) ，并且彼此平行堆叠，那么这个问题就会变得极其困难 (指数级难度) 。在最坏的情况下，学习 \(d\) 维空间中的 \(k\) 个高斯混合分布需要 \(d^{O(k)}\) 的时间。

最近的研究试图寻找一个中间地带。如果我们假设混合权重 (即属于每个分量的群体比例) 不是极小的，会发生什么？研究人员发现了一些在准多项式时间 (Quasi-polynomial time) 内运行的算法，具体来说是 \(d^{O(\log(1/w_{\min}))}\)。

这引出了一篇引人入胜的新论文: “On Learning Parallel Pancakes with Mostly Uniform Weights” (关于学习主要是均匀权重的平行煎饼问题) 。

这项研究解决了两个基本问题:

  1. 目前的准多项式速度限制是真实的吗? 如果权重完全均匀 (即均为 \(1/k\)) ，我们能做得更好吗？
  2. 如果权重是“主要是”均匀的呢? 如果大多数分量是平衡的，但有少数异常分量具有任意权重，情况会怎样？

在这篇文章中，我们将深入探讨这篇论文。我们将探讨为什么“平行煎饼”如此难以检测，并证明即使权重均匀，我们也会遇到计算墙。然后，我们将着眼于一个新的巧妙算法结果，表明如果权重主要是相等的，问题就会变得容易得多。

背景: 煎饼的问题

要理解这篇论文的贡献，我们首先需要定义“平行煎饼” (Parallel Pancakes) 问题。

想象一下你在高维空间 (\(d\) 维) 中有一个数据分布。

  • 原假设 (The Null Hypothesis, \(H_0\)) : 数据仅仅是标准高斯噪声 \(\mathcal{N}(0, I)\)。它看起来像一个以原点为中心的模糊超球体。
  • 备择假设 (The Alternative Hypothesis, \(H_1\)) : 数据来自 \(k\) 个高斯的混合。然而，这些不是普通的高斯分布。它们的均值都沿着一个未知的方向 \(v\) 排列，并且它们沿着同一个方向被压扁 (squashed) 。在所有正交方向上，它们看起来就像标准高斯分布。

因为它们被压扁并沿着一条线堆叠，所以它们看起来就像漂浮在高维空间中的一叠煎饼。

挑战在于区分这两种情况。这就是所谓的*非高斯分量分析 (Non-Gaussian Component Analysis, NGCA) *问题。如果煎饼堆叠得恰到好处，它们沿方向 \(v\) 的组合密度几乎可以完美地模仿标准高斯分布。如果混合分布与标准高斯分布的前 \(m\) 阶矩匹配，那么识别隐藏方向 \(v\) 大约需要 \(d^{m}\) 个样本或查询。

SQ 模型

作者使用统计查询 (Statistical Query, SQ) 模型来分析这个问题。SQ 算法不查看单个数据点，而是提出这样的问题: “这个函数 \(f(x)\) 在该分布上的期望值是多少？”预言机 (Oracle) 会在一定的容差 \(\tau\) 内返回答案。

这个模型非常强大，因为它涵盖了几乎所有的标准技术 (SGD、谱方法、矩匹配) 。在 SQ 模型中证明下界是该问题对于任何抗噪算法都具有计算困难性的强有力指标。

第一部分: 坏消息 (SQ 下界)

这篇论文的第一个主要贡献是一个下界 。 之前的算法对于最小权重 \(w_{\min}\) 是 \(k\) 的多项式的情况，达到了 \(d^{O(\log k)}\) 的复杂度。作者提出疑问: 如果我们强制所有权重完全相等 (\(w_i = 1/k\)) ，从而使问题变得“更简单”，我们能得到多项式时间的算法吗？

答案是否定的。

论文中的定理 1.2 指出，即使权重均匀，任何 SQ 算法也需要 \(d^{\Omega(\log k)}\) 的复杂度。这证明了现有的准多项式算法在本质上是最优的。

策略: 矩匹配设计

为了证明这种困难性，作者构建了一个“坏”的分布。他们需要在 1D 空间中找到一组 \(k\) 个点 (代表煎饼的中心) ，使得这些点上的均匀分布能够匹配标准高斯分布的前 \(m = \Omega(\log k)\) 阶矩。

如果存在这样的分布，他们就可以创建一个平行煎饼实例，该实例在直到第 \(m\) 阶矩上都“看起来”像标准高斯分布。标准的 SQ 结果告诉我们，区分这种混合分布需要 \(d^{\Omega(m)}\) 的时间。

该证明依赖于设计理论 (Design Theory) 。 具体来说，他们需要证明存在一个支撑在区间上的离散分布，该分布与高斯分布的矩相匹配。

这里的关键指标是 \(K_t\)，该值限制了区间上多项式的最大值与最小值的比率。如果这个比率被限制在 \(2^{O(t)}\) 以内，则存在大小为 \(t\) 的设计。

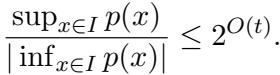
Supremum over infimum ratio inequality for polynomials

为了限制这个比率，作者利用了埃尔米特多项式 (Hermite polynomials) 的性质。他们将任意多项式 \(p(x)\) 在埃尔米特基底下展开。

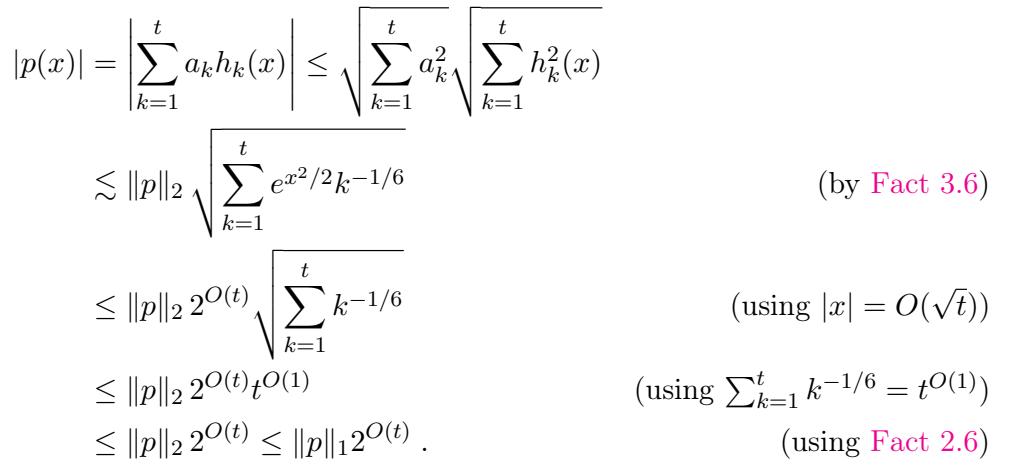
Polynomial expansion in Hermite basis and bounds

利用埃尔米特多项式有界 (由高斯密度加权) 的事实，并应用反集中不等式 (anti-concentration inequalities) , 他们证明了多项式在该区间内相对于其范数不会保持“太小”。

具体来说，他们使用 Carbery-Wright 不等式来确保多项式在零附近不会太“平坦”:

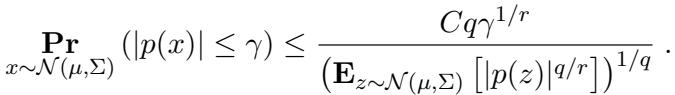
Carbery-Wright inequality application

通过结合这些界限，他们证明了确实可以以某种方式堆叠 \(k\) 个均匀的煎饼，使其匹配标准高斯分布的 \(\log k\) 阶矩。因此，该问题仍然具有准多项式级的困难度。

第二部分: 好消息 (主要是均匀的权重)

虽然均匀权重的情况很困难，但这篇论文的第二个贡献提供了一个新的视角。之前最好的算法的复杂度依赖于 \(1/w_{\min}\)。如果哪怕只有一个分量的权重极小 (例如 \(2^{-k}\)) ，运行时间就会爆炸式增长到指数级。

作者提出了一个“主要是均匀”的设定:

  • \(k'\) 个分量具有任意权重。
  • 其余 \(k - k'\) 个分量具有相等的权重。

定理 1.3 提出了一种算法，其样本复杂度大约为 \((kd)^{O(k' + \log k)}\)，可以解决这个测试问题。

这是一个显著的改进，因为它在困难和容易的区域之间进行了插值。如果你只有少数几个权重“怪异”的分量，复杂度不会因为它们的权重有多小而爆炸——它只取决于有多少个这样的分量 (\(k'\)) 。

核心逻辑: 矩匹配的不可能性

该算法之所以有效，是因为一个关键的结构性洞察: 一个“主要是均匀”的混合模型无法长期伪装成高斯模型。

虽然完全任意的混合模型可能匹配高达 \(k\) 阶的矩，而完全均匀的混合模型可能匹配到 \(\log k\) 阶，但只有 \(k'\) 个任意权重的混合模型只能匹配到 \(m \approx O(k' + \log k)\) 阶的矩。

如果混合模型无法匹配第 \((m+1)\) 阶矩，算法可以通过从数据中估计矩张量并将其与标准高斯张量进行比较来检测出来。

证明: 限制矩

他们如何证明匹配超过 \(O(k' + \log k)\) 阶矩是不可能的？这是论文的技术核心。

设 \(A\) 为煎饼中心的离散分布。假设 \(A\) 匹配标准高斯分布的前 \(m\) 阶矩。我们定义一个多项式 \(p(x)\)，它在 \(k'\) 个权重任意的位置上消失 (值为零) 。

然后我们观察函数 \(f(x) = x^t p(x)\)。目标是通过观察期望的比率来推导出一个矛盾:

\[ \frac{\mathbb{E}_{x \sim A}[f^2(x)]}{(\mathbb{E}_{x \sim A}[f(x)])^2} \]

首先，作者推导了这个比率的上界。因为 \(p(x)\) 将任意权重部分清零，所以期望只取决于均匀权重部分。这导致了如下不等式:

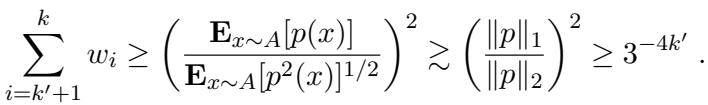
Inequality bounding the sum of weights

本质上，因为权重是均匀的 (大约是 \(1/k\)) ，这个比率不能太大。

接下来，他们需要一个下界 。 为了反证，他们假设分布 \(A\) 匹配高斯分布 \(\mathcal{N}(0,1)\) 的矩。这允许他们将对 \(A\) 的期望替换为对高斯分布的期望 (加上一个微小的误差项 \(\lambda\)) 。

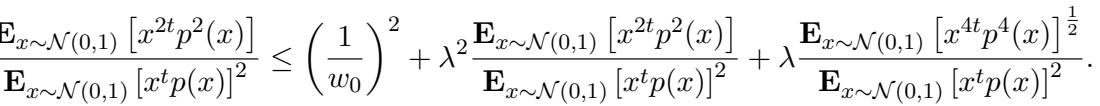
Inequality relating expectations over A and Normal distribution

为了得到矛盾，他们需要证明左边 (LHS，高斯测度下的比率) 实际上非常大——比均匀权重允许的上界要大得多。

这需要证明多项式 \(x^{2t}p^2(x)\) 的期望相对于 \(x^t p(x)\) 期望的平方来说很大。

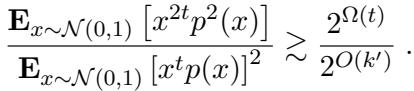
Ratio lower bound of Gaussian expectations

连续 AM-GM 技巧

为了证明图 16 (上图) 中的不等式，作者使用了积分形式的算术平均数-几何平均数 (AM-GM) 不等式这一优美的分析技巧。

他们分析了多项式在一个特定区间 \(I = [0.9\sqrt{2t}, 1.1\sqrt{2t}]\) 上的积分。他们需要在这个区域内限制 \(p(x)\) 的“能量”下界。

利用连续 AM-GM 不等式，他们将 \(p^2(x)\) 的算术平均数与几何平均数联系起来，后者涉及 \(\ln|p(x)|\) 的积分:

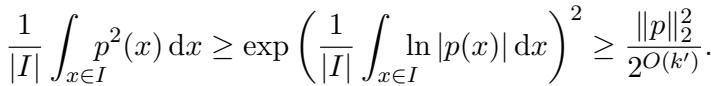
AM-GM inequality applied to integral of polynomial

这将问题转化为限制多项式对数的积分。由于 \(p(x) = \prod (x - \mu_i)\)，对数分解为对数之和:

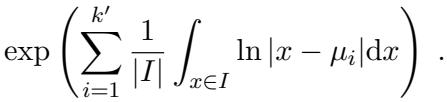
Exponential of sum of log integrals

然后，作者针对根 \(\mu_i\) 相对于区间 \(I\) 的位置进行了详细的分类讨论。通过对 \(\ln|x - \mu_i|\) 进行积分，他们证明了多项式在该区间上的“几何平均数”不会太小。

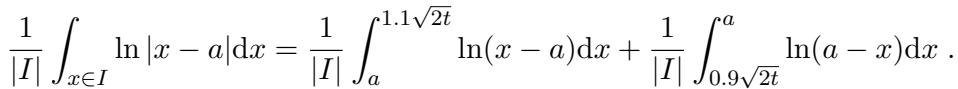
Integral calculation of log term

将这些贡献相加并取指数后，他们得到了比率分子的下界。

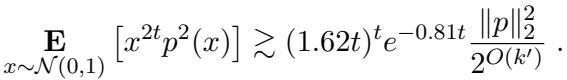
Lower bound of Gaussian expectation of x^2t p^2(x)

将其与分母的上界 (使用标准高斯超压缩性 Gaussian hypercontractivity) 相结合，他们迫使该比率至少为 \(2^{\Omega(t)}\)。

由于从权重推导出的上界大约是 \(k\)，而下界是关于 \(t\) 的指数，我们得到了 \(t\) 的限制:

\[ t \lesssim \log k + k' \]

这证明了你无法匹配超过这个阈值的矩！

算法

掌握了矩必须在某个阶数 \(m \approx O(k' + \log k)\) 处存在差异的知识后，算法就变得 (概念上) 简单明了了。

  1. 计算张量间隙: 我们知道对于某个 \(i \leq m\)，我们的数据的第 \(i\) 阶矩张量与标准高斯张量之间的差异是显著的。

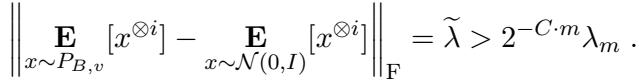
Frobenius norm of tensor difference

  1. 采样和验证: 算法抽取样本并计算经验张量。

  2. 阈值判定: 如果经验张量与高斯张量的差异超过特定阈值 (源自理论间隙) ，我们拒绝原假设并宣布“这是煎饼！”

这里有一个技术上的注意事项: 样本复杂度取决于数据是否表现良好 (集中) 。为了确保这一点，作者增加了一个检查步骤，以验证没有数据点距离原点过远，否则可能会搞乱张量估计。

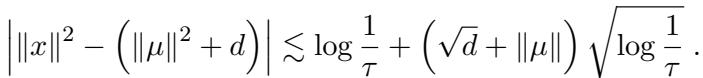
Concentration bound for norm of x

这确保了经验平均值能够快速收敛到真实期望。

结论

论文 “On Learning Parallel Pancakes with Mostly Uniform Weights” 为学习具有共同协方差的 GMM 问题提供了一个严密的解决方案。

  1. 局限性: 我们现在知道，学习平行煎饼的准多项式时间复杂度不仅仅是我们当前算法的人为产物——它通过 SQ 下界植根于问题的几何结构中。即使是均匀权重也无法拯救我们。
  2. 插值: 然而，这篇论文为“混乱”的数据提供了一条充满希望的道路。如果我们有一个均匀噪声/分量作为背景，其中点缀着少量任意信号，我们可以高效地检测到它们。复杂度随任意分量的数量 (\(k'\)) 扩展，而不是随它们的权重扩展。

这项工作完美地结合了组合数学 (设计理论) 、分析 (多项式逼近) 和统计学 (SQ 模型) ，勾勒出了高维空间中计算可学习性的边界。