如果你处理过真实世界的数据集，尤其是在医疗或金融领域，你一定体会过缺失值带来的痛苦。你设计了一个完美的模型，在清洗过的数据上进行了训练，并准备将其部署。但到了“测试阶段” (即模型面对真实用户的时刻) ，问题来了。用户跳过了表单上的某个问题，或者医生没有开具某项特定的检测。突然之间，你的模型就像一只眼睛失明了一样，无法正常工作。

我们该如何处理这个问题？标准的做法通常有两条路: 插补 (根据平均值或模式猜测缺失值) 或缺失指示符 (添加一个标记告诉模型“这个数据缺失了”) 。

虽然这些方法在计算上行得通，但它们引入了一个隐患: 可靠性和可解释性 。 如果一个模型因为猜测了一个缺失的血压值而预测某人有高心脏病风险，医生能信任它吗？

在论文 《Prediction Models That Learn to Avoid Missing Values》 (学习避免缺失值的预测模型) 中，研究人员 Stempfle、Matsson、Mwai 和 Johansson 提出了一个令人耳目一新的替代方案。他们不是教模型去猜测不存在的数据，而是教模型从一开始就避免需要这些缺失数据。

这种方法被称为缺失避免 (Missingness-Avoiding，简称 MA) 学习 , 它从根本上改变了机器学习的目标: 不再仅仅追求纯粹的准确性，而是寻求准确性与数据可用性之间的平衡。

“先插补再回归”的问题

为了理解为什么需要 MA 学习，我们先看看现状。经典的策略是“先插补再回归 (impute-then-regress) ”。你填补空白 (插补) ，然后运行你的预测模型。

当数据是结构性缺失时，问题就出现了。在医疗领域，医生不会随机开具检测单。他们是根据症状开具检测的。如果某项检测缺失，这种“缺失”本身就是一种信息。如果我们简单地填入平均值 (零插补或均值插补) ，我们可能会掩盖决策的逻辑。

此外，标准的决策树是“贪婪”的。它们会抓取当前能最好地划分数据的特征，而不考虑该特征在未来是否昂贵、具有侵入性或可能缺失。

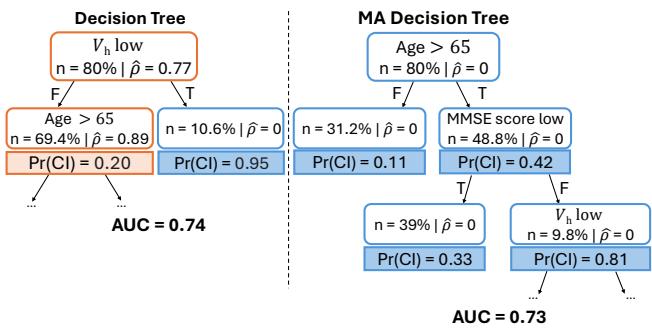
标准决策树与缺失避免树的对比。

请看上面的 图 1 。 左边是一棵标准的决策树。它的 AUC (准确率指标) 达到了 0.74。然而，它的第一个问题依赖于“海马体体积” (\(V_h\)) ，这是一个源自 MRI 扫描的数值。在这个数据集中，77% 的患者都缺失这个值 (\(\hat{\rho} = 0.77\)) 。如果患者没有做 MRI，模型就只能依赖插补值或默认路径，这是有风险的。

右边是一棵缺失避免 (MA) 树 。 它达到了几乎相同的准确率 (AUC 0.73) ，但它首先询问的是“年龄”——一个几乎从不缺失的值。只有当患者超过 65 岁且认知评分较低时，它才会询问 MRI 扫描结果。对于许多患者，它根本不需要询问 MRI。这个模型已经“学会”了 MRI 经常缺失，并构建了相应的决策逻辑，以便尽可能避开它。

MA 框架: 一个新的目标

我们如何在数学上强制模型像右边的树那样行事？作者在标准损失函数中引入了一个新的正则化项。

通常，我们训练模型是为了最小化预测值与真实标签之间的差异 (损失，\(L\)) 。作者为此增加了一个针对缺失依赖度 (Missingness Reliance, \(\rho\)) 的惩罚项。

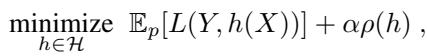
缺失避免目标函数。

在这里，\(\alpha\) (alpha) 是控制权衡的超参数。

  • 如果 \(\alpha = 0\)，模型会忽略缺失情况，只关注准确性 (标准行为) 。
  • 随着 \(\alpha\) 增加，模型因依赖测试时可能缺失的特征而受到的惩罚也会增加。

定义缺失依赖度 (\(\rho\))

但是 \(\rho\) 究竟是什么？它被定义为模型需要一个结果为“na” (不可用) 的值的概率。

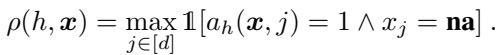
缺失依赖度的定义。

简单来说，对于特定的输入 \(\mathbf{x}\)，如果模型的逻辑路径需要特征 \(j\) (\(a_h(\mathbf{x}, j) = 1\)) ，而特征 \(j\) 恰好缺失 (\(x_j = \mathbf{na}\)) ，那么依赖度就是 1。否则，就是 0。

目标是在整个数据集上最小化这种依赖的期望值。

避免策略

论文指出了模型可以避免缺失值的与其主要方式，如下图所示:

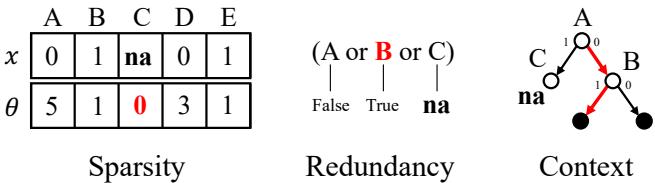
避免缺失值的三种策略: 稀疏性、冗余性和上下文。

  1. 稀疏性 (Sparsity，左图) : 模型干脆停止使用那些频繁缺失的特征。这在像 LASSO 这样的线性模型中很常见。
  2. 冗余性 (Redundancy，中图) : 模型学习替代规则。如果 \(A\) 缺失，检查 \(B\) 或 \(C\) 是否能提供相同的信息。
  3. 上下文 (Context，右图) : 这正是决策树大显身手的地方。模型改变提问的顺序。它只在绝对必要且数据很可能存在的特定上下文 (分支) 中，才询问可能缺失的特征 (如 MRI 结果) 。

让我们深入了解研究人员是如何针对特定算法实现这一点的。

1. MA-DT: 缺失避免决策树

决策树天生适合上下文避免。标准决策树根据基尼不纯度 (Gini impurity) 等标准来划分数据。MA-DT 修改了这个划分标准。

当评估特征 \(j\) 作为一个潜在的划分点时，算法会计算标准的不纯度减少量，但会减去一个与特征 \(j\) 在当前节点缺失频率成比例的惩罚项。

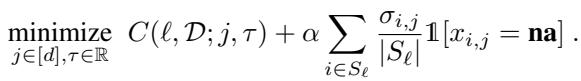
MA-DT 的正则化划分标准。

在这个公式中:

  • \(C\) 是标准成本 (不纯度) 。
  • \(\alpha\) 是我们的正则化强度。
  • 求和部分计算了当前节点 (\(S_{\ell}\)) 中有多少样本缺失了特征 \(j\)。

这个简单的改变迫使决策树倾向于在树的上层使用“安全”、可用的特征 (如年龄或性别) ，将“高风险”、经常缺失的特征推到更深层，那里涉及的样本更少。

2. MA-LASSO: 稀疏线性模型

对于线性模型 (如逻辑回归) ，不存在“上下文”的概念。本质上你是一次性使用所有选定的特征。在这里，避免缺失依赖于稀疏性 。

作者修改了经典的 LASSO (L1 正则化) 目标函数。标准 LASSO 惩罚系数的绝对大小 (\(|\theta|\)) ，以将无关特征驱动为零。MA-LASSO 则根据每个特征的缺失率对这个惩罚进行加权。

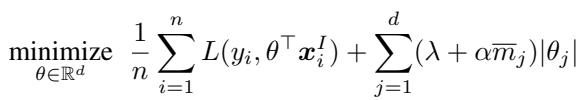
MA-LASSO 目标函数。

这里，\(\bar{m}_j\) 是特征 \(j\) 缺失的比例。如果一个特征 90% 的时间都缺失，它的惩罚就会非常大。模型会非常努力地将其系数 \(\theta_j\) 设为零，实际上就是将其移除，除非它具有极强的预测能力。

理论洞察: ODDC 规则

这篇论文最迷人的贡献之一是对观测确定性数据收集 (Observed Deterministic Data Collection, ODDC) 规则的形式化。

在许多系统中，数据并非随机缺失；它是因设计而缺失。

  • *例子: * 男性患者的“妊娠测试结果”变量总是缺失的。
  • *例子: * 只有当“初步筛查”为阳性时，才会有“后续实验室结果”。

作者将 ODDC 规则定义为一种蕴含关系: “如果变量 \(X_T\) 的值在集合 \(A\) 中，则变量 \(j\) 会被观测到。”

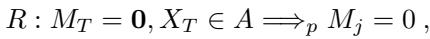
ODDC 规则的定义。

这为什么重要? 作者证明，如果结果 \(Y\) 通过这些规则依赖于输入 \(X\)，那么理论上可以构建一个零缺失依赖度 (\(\rho=0\)) 的模型，且不牺牲预测准确性。

MA-DT (决策树) 非常适合这种情况。通过调整 \(\alpha\)，树会自然地学习数据收集过程的结构。它学会了在询问“妊娠测试”前先检查“性别”，或者在询问“实验室结果”前先检查“初步筛查”。

实验与结果

研究人员在六个真实的医疗和金融数据集上测试了他们的框架，包括 NHANES (高血压预测) 和 ADNI (阿尔茨海默病诊断) 。他们使用不同的插补策略，将 MA 模型与标准基线模型 (逻辑回归、随机森林、XGBoost) 进行了比较。

关键发现: “免费的午餐”

结果表明，你通常可以大幅减少对缺失值的依赖，而几乎不会导致准确率 (AUROC) 下降。

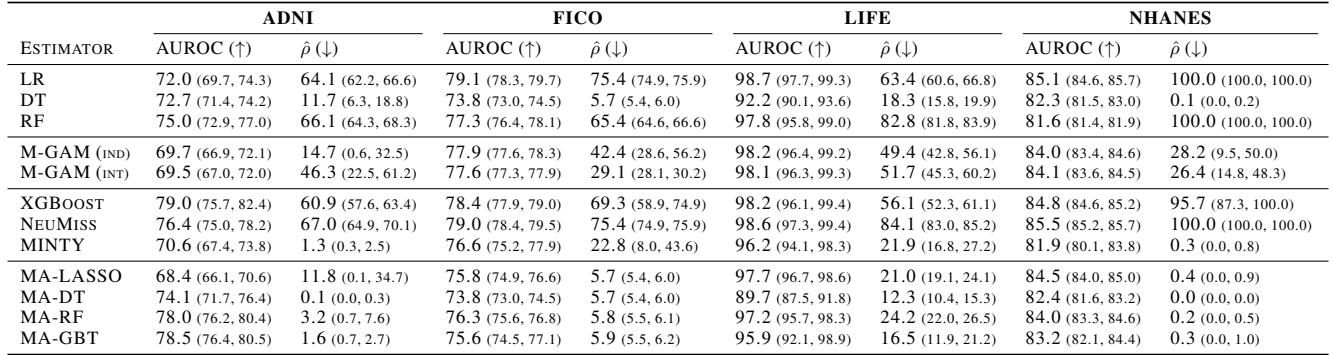
比较 AUROC 和缺失依赖度的结果表。

查看 表 1 (Table 1) :

  • 在 NHANES 数据集中，标准逻辑回归 (LR) 100% 的时间都依赖于缺失值 (\(\hat{\rho} = 100.0\)) 。
  • MA-LASSO 模型达到了相当的准确率 (AUROC ~84.5 vs 85.1) ，但将缺失依赖度降到了仅 0.4% 。
  • 同样，对于 ADNI , 标准决策树 (DT) 的依赖度为 11.7%，而 MA-DT将其降至 0.1% , 且 AUC 甚至略高一点 (74.1 vs 72.7) 。

这证实了假设: 标准模型是“懒惰”的。它们抓取混乱的特征是因为这些特征在训练期间提供了边际收益，却忽略了缺失带来的代价。MA 模型迫使它们寻找更干净、更稳健的路径。

权衡曲线

当然，有时避免缺失数据确实会牺牲准确性。参数 \(\alpha\) 允许从业者驾驭这种权衡。

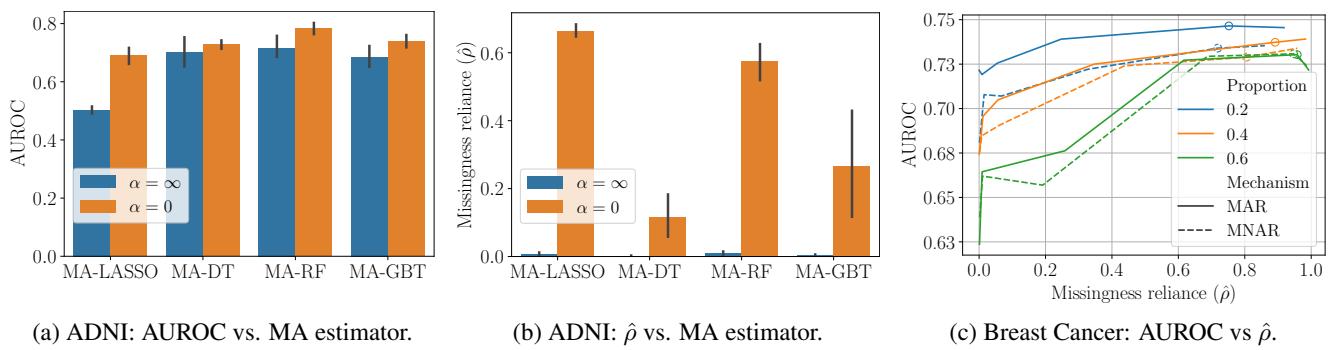
准确性与缺失依赖度之间的权衡。

在 图 4 (c) (右侧曲线) 中，我们看到了 MA-LASSO 在具有合成缺失值的乳腺癌数据集上的表现。

  • 当我们允许更多的缺失依赖 (在 x 轴上向右移动) 时，准确率 (AUROC) 会提高。
  • 然而，曲线在开始时很陡峭，然后变平。这意味着我们可以消除大量的缺失依赖，而只需付出极小的准确率“代价”。

解释模型

MA 模型 (特别是树模型) 的一个主要优势是可解释性。我们可以直观地看到模型是如何避开缺失数据的。

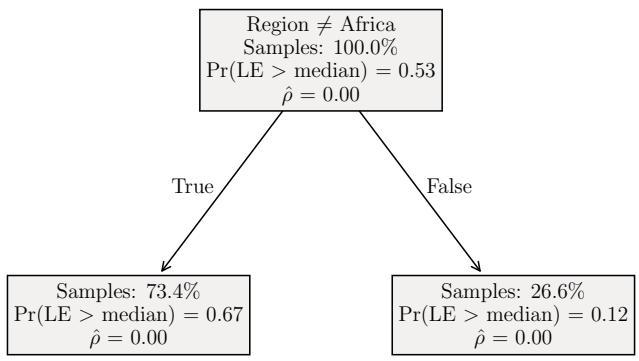
不同 alpha 值下学习到的决策树可视化。

图 6 展示了在 LIFE 数据集 (预测预期寿命) 上训练的三棵树:

  1. (a) \(\alpha = 0\) (标准树) : 立即根据“成人死亡率”和“婴儿死亡数”进行划分。如果这些数据缺失，模型就卡住了。
  2. (b) \(\alpha = \alpha^*\) (平衡的 MA 树) : 首先根据“成人死亡率”划分，但随后使用“地区” (Region，从不缺失) 来处理死亡率数据可能缺失的情况。它平衡了准确性与可用性。
  3. (c) \(\alpha = \infty\) (最大避免) : 仅根据“地区”进行划分。它从不询问死亡率数据。这具有零缺失依赖度 (\(\rho=0\)) ，但正如预期的那样，准确率较低 (AUC 0.67 vs 0.90) 。

中间地带 (b) 通常是奇迹发生的地方。

结论

“缺失避免”框架为我们思考如何处理不完整数据的监督学习提供了一个引人注目的视角。作者不再将缺失值视为需要在建模之前解决的数据清洗问题 (通过插补) ，而是将其视为需要在训练期间解决的建模约束。

对于学生和从业者来说，主要启示很明确:

  1. 插补并非无害: 它引入了偏差和不透明性。
  2. 上下文很重要: 在树模型中，特征的顺序决定了你是否需要一个缺失值。
  3. 你有选择权: 你不必接受一个依赖于你可能没有的数据的模型。通过惩罚缺失依赖度，你可以构建稳健、可解释且“测试时安全”的模型。

这种方法给我们的模型不仅能预测未来，还能理解当前数据的局限性，从而使它们在现实世界的部署中更加安全。