引言

在人工智能飞速发展的版图中，每当一个新的大语言模型 (LLM) 发布时，都会出现一个关键问题: 它比其他的更好吗?

为了回答这个问题，社区转向了“模型竞技场 (Model Arenas) ”。像 Chatbot Arena 这样的平台允许用户同时向两个匿名模型提问，并投票选出哪个回答更好。这是一个数字角斗场，模型们在这里争夺霸权。为了将这些胜负量化为排行榜，研究人员依赖于 ELO 等级分系统——这与排名国际象棋选手和视频游戏竞技者的算法相同。

然而，将一个为国际象棋设计的系统应用于 LLM 会带来严重的问题。标准 ELO 评级在应用于众包数据时众所周知地不稳定。它们会根据对战发生的顺序而波动，更重要的是，它们视每位人类投票者具有同等能力。无论标注者是领域专家还是随机乱点的路人，ELO 算法赋予他们投票的权重都是一样的。

在这篇深度文章中，我们将探讨一篇提出解决方案的新研究论文: 稳定竞技场框架 (Stable Arena Framework) 。 我们将详细解析研究人员如何用一种称为 m-ELO 的稳健统计方法替换不稳定、迭代的标准 ELO，以及他们如何进一步将其升级为 am-ELO——一个不仅对模型进行排名，还能对“裁判”进行评判的系统。

当前竞技场存在的问题

在理解解决方案之前，我们必须先了解为什么当前系统是有缺陷的。

标准 ELO 系统以迭代方式更新模型的分数。每次对战后，胜者得分，败者扣分。分数交换的多少取决于他们当前评级的差异。

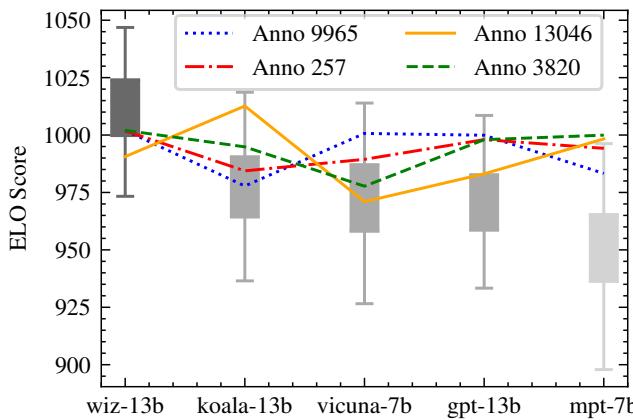
如图 Figure 1 所示，标准 ELO 分数可能会剧烈波动。图表显示了 vicuna-7b 和 koala-13b 等模型的分数波动。显著的误差条和“跳跃”的线条表明，计算出的分数很大程度上取决于计算发生的时间以及记录的特定顺序。

造成这种不稳定性的主要罪魁祸首有两个:

1. 顺序敏感性: ELO 是一种动态算法。如果你打乱对战历史并重新运行计算，通常会得到不同的最终分数。
2. 标注者差异: 人类评估是主观的。一个人可能看重代码的准确性，而另一个人可能看重礼貌的语气。更糟糕的是，一些标注者可能是垃圾信息发送者或机器人。标准 ELO 系统忽略了这些个体差异，假设每次交互中都是一个“完全平均”的人类。

基础: 经典 ELO 更新

为了修复 ELO，我们首先需要看看它的数学引擎。在传统系统中，当模型 \(i\) 与模型 \(j\) 对战时，我们使用以下公式更新它们的分数 (\(R\)) :

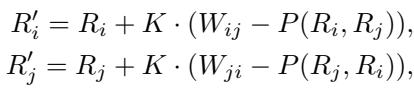
这里，\(K\) 是缩放因子 (分数变化的速度) ，而 \(P(R_i, R_j)\) 是模型 \(i\) 获胜的预期概率。系统会查看实际结果 \(W_{ij}\) (1 代表胜利，0 代表失败) 与预期概率之间的差异。

这种方法对于按顺序进行的体育比赛效果很好，但在 LLM 评估中，我们要处理的通常是一个包含数千次过往对战的静态数据集。将这些静态数据视为顺序流引入了人为的“时间”依赖性，导致了我们在 Figure 1 中看到的不稳定性。

解决方案第一部分: m-ELO (极大似然估计)

研究人员建议从迭代更新转向全局优化。与其一次一场比赛地更新分数，为什么不审视整个对战历史，找到最能解释这些数据的一组分数呢？

这种方法被称为 m-ELO 。 它使用极大似然估计 (MLE) 来寻找模型评级。

其逻辑体现在这个对数似然函数中:

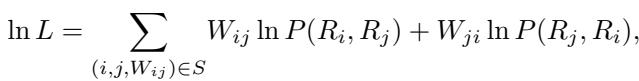
简单来说，这个方程计算的是在给定一组特定模型分数的情况下，观察到的胜负结果发生的可能性有多大。目标是最大化这个值。通过使用梯度下降法求解该方程，结果变得与顺序无关 。 无论你如何打乱对战记录，m-ELO 方法都会收敛到相同的评级。

这解决了第一个问题 (因顺序导致的不稳定性) ，但它没有解决第二个问题: 人类标注者的不可靠性。

解决方案第二部分: am-ELO (标注者建模)

这篇论文最重要的贡献是 am-ELO 。 研究人员从心理测量学中的 项目反应理论 (IRT) 汲取灵感，该理论用于在考试评分时同时考虑问题的难度和考生的能力。

在竞技场的背景下，研究人员意识到他们可以对 标注者的能力 (\(\theta_k\)) 进行建模。

直觉

在标准 ELO 中，通常有一个常数参数记为 \(C\) (或嵌入在 Logistic 函数中) ，它决定了技能差异对获胜概率的影响程度。研究人员意识到这不应该是一个常数。

• 如果标注者是 专家 (\(\theta\) 很高) ，他们可以轻易区分出一个稍好的模型和一个稍差的模型。
• 如果标注者是 随机或困惑的 (\(\theta\) 接近 0) ，他们的投票与模型质量的真实差异相关性不高。
• 如果标注者是 恶意或有偏见的 (\(\theta\) 为负) ，他们可能会持续投票给更差的模型。

新的概率函数

研究人员修改了概率函数，为每个特定的标注者 \(k\) 引入了这个新参数 \(\theta_k\):

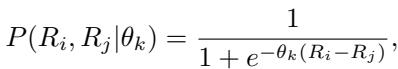
这个微小的改变意义深远。它意味着获胜的预期概率不仅取决于模型的技能差异 (\(R_i - R_j\)) ，还取决于标注者的可靠性 (\(\theta_k\)) 。

架构对比

我们可以在下面直观地看到传统方法与这个新框架的区别:

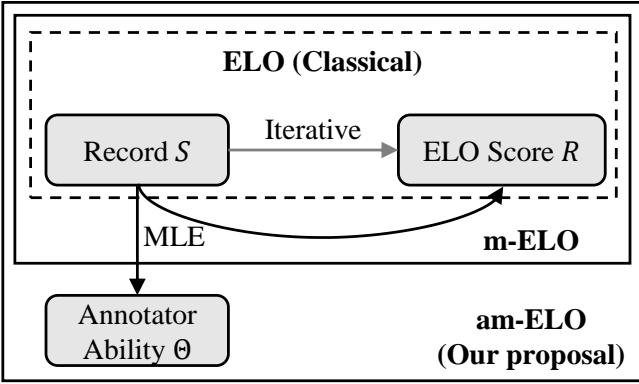
如图 Figure 2 所示，经典方法 (顶部) 纯粹在记录和分数之间循环。新的 am-ELO 方法 (底部) 采取整体视角，将记录和分数输入到极大似然估计引擎中，该引擎同时输出 模型分数 和 标注者能力 。

优化

为了训练这个系统，研究人员使用梯度下降来更新模型评级 (\(R\)) 和标注者参数 (\(\theta\)) 。梯度如下所示:

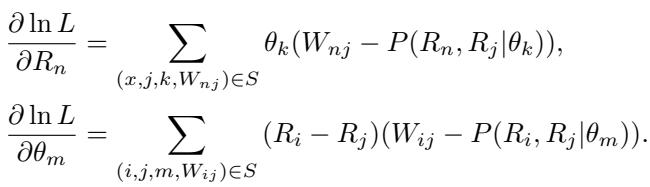
上面的方程根据模型是赢是输来更新其分数，并由标注者的可靠性 (\(\theta_k\)) 进行加权。下面的方程根据标注者的投票是否与模型的共识排名 (\(R_i - R_j\)) 一致来更新标注者的可靠性。

这创造了一个良性循环: 更好的模型排名有助于识别优秀的标注者，而优秀的标注者有助于改进模型排名。

实验与结果

研究人员在 Chatbot Arena 数据集上测试了他们的框架，该数据集包含 33,000 个对话和投票。

1. 更好的拟合与预测

首先，他们检查了不同方法拟合数据的效果。更低的“Loss (损失) ”意味着模型能更好地解释对战的现实情况。

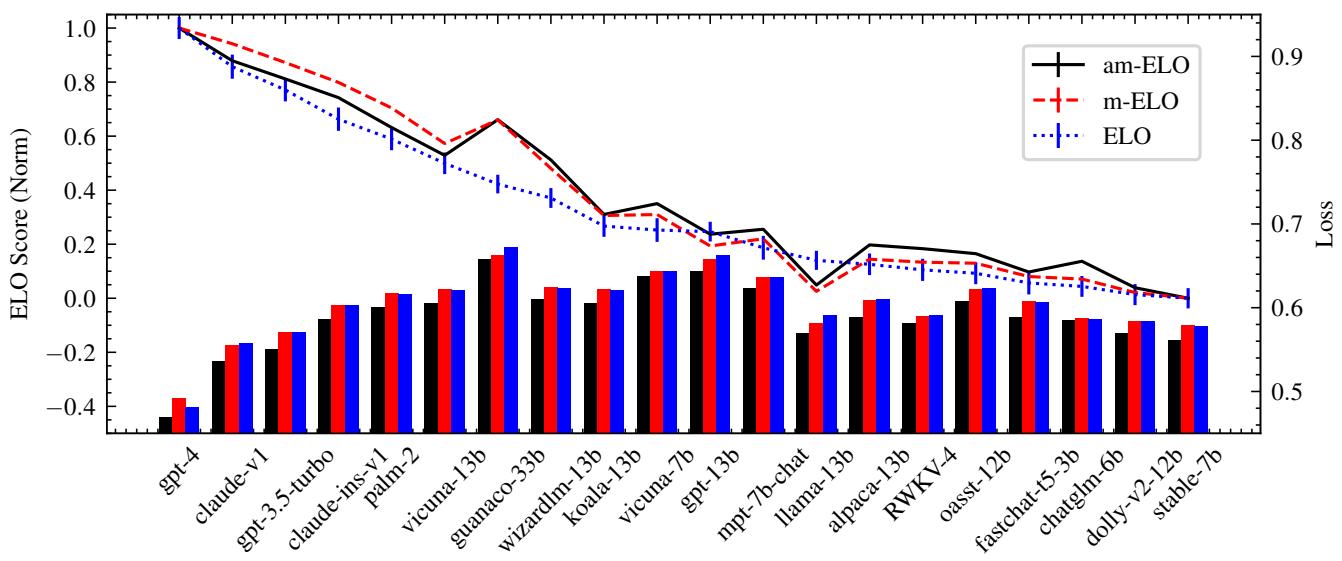
在 Figure 3 中，右侧的柱状图显示了损失。你可以看到 am-ELO (黑线) 的损失显著低于标准 ELO (蓝色) 或 m-ELO (红色) 。这证明了考虑标注者差异为竞技场提供了更准确的数学模型。

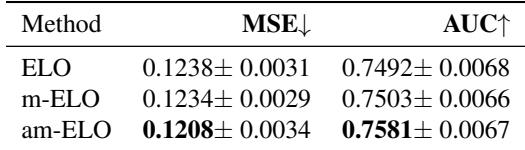
此外，下方的 Table 2 显示 am-ELO 在预测未见过对战的结果方面表现更好 (更高的 AUC 和更低的均方误差) 。

2. 修正排名: Vicuna 与 Koala 的案例

最有趣的发现之一是 am-ELO 如何修正特定的排名错误。在标准 ELO 系统中，名为 koala-13b 的模型排名高于 vicuna-7b。然而，社区中的许多人认为 Vicuna 是更强的模型。

为什么标准 ELO 会搞错？

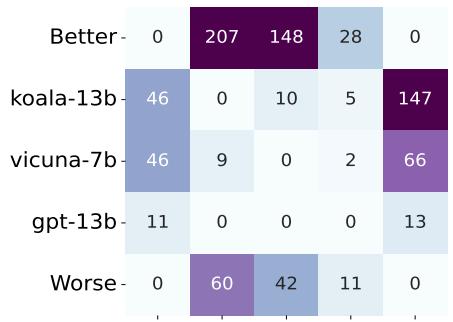
Figure 4 揭示了真相。koala-13b 赢了很多“Worse (更差) ”的模型 (弱对手) 。vicuna-7b 与弱对手交战较少，但在对抗“Better (更好) ”的模型时表现稳健。

标准 ELO 盲目地奖励累积胜场。 am-ELO 通过考虑全局背景和标注者质量，正确地识别出 vicuna-7b 实际上是更强的模型，并将排行榜调整为符合人类直觉的结果。

3. 稳定性与收敛性

“稳定竞技场框架”中的“稳定”不仅仅是个名字。研究人员追踪了训练过程中排名的一致性。

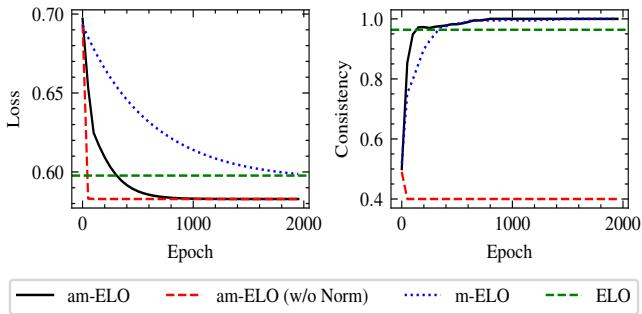
Figure 5 显示了一致性 (右图) 。 am-ELO 方法 (实黑线) 开始时一致性较低，但迅速攀升至接近 1.0。这表明无论初始化如何，该方法都能可靠地收敛到同一组分数。注意红色的虚线 (am-ELO w/o Norm) ；如果不归一化标注者能力的总和，系统会变得不稳定，这证明归一化是算法中至关重要的一步。

4. 检测恶意标注者

最后，研究人员模拟了对竞技场的“攻击”。他们引入了虚拟标注者，这些标注者会随机翻转投票、投平局票，或者试图颠倒排名。

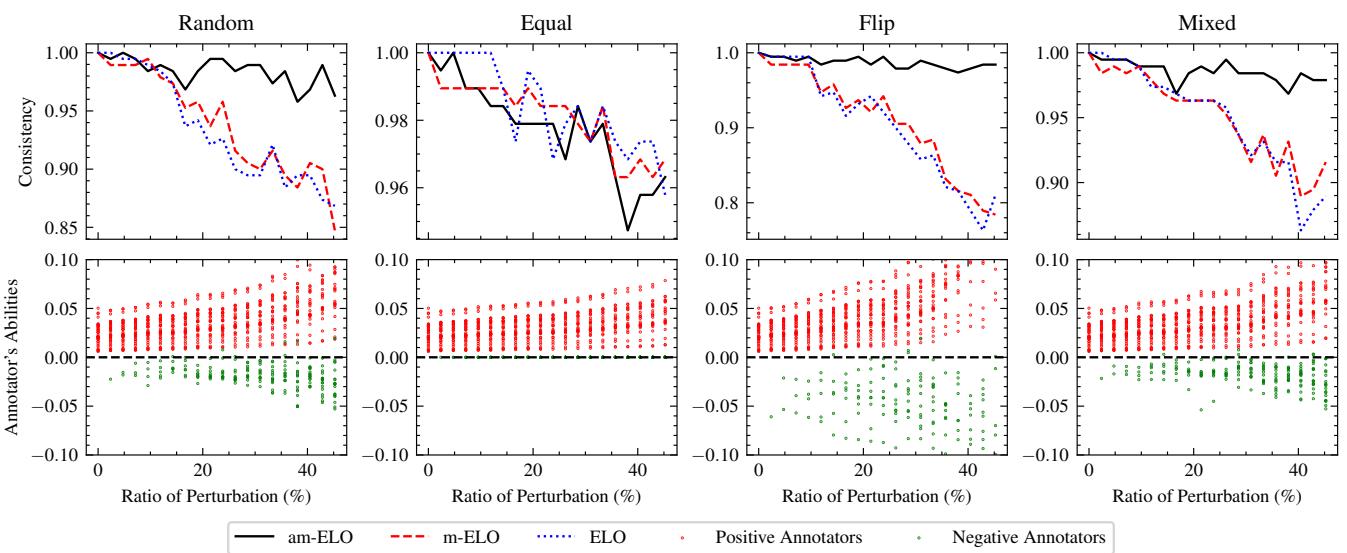
Figure 6 展示了系统的鲁棒性。

• 上图 (一致性) : 即使随着坏标注者 (扰动) 的比例增加，与标准 ELO (蓝色点线) 相比，am-ELO (黑线) 仍保持较高的排名一致性。
• 下图 (标注者能力) : 红点代表正常标注者，绿点代表模拟攻击者。注意绿点是如何骤降至零以下的吗？am-ELO 系统成功识别了攻击者并分配给他们负的能力分，有效地中和了他们的恶意投票。

结论

“稳定竞技场框架”代表了我们在评估 AI 方式上的重大成熟。随着大语言模型日益融入社会，我们用来评判它们的指标必须严谨。

通过从简单的迭代更新转变为极大似然估计方法( m-ELO )，我们解决了顺序敏感性问题。通过整合心理测量学原理来对裁判本身进行建模( am-ELO )，我们解决了人类差异性问题。

该框架实现了一个更公平、更稳健的排行榜，其中:

1. 模型排名稳定 且可复现。
2. 标注者可靠性透明 , 允许平台奖励优秀的裁判并过滤掉糟糕的裁判。
3. 复杂的动态 (如通过战胜弱对手刷胜场) 得到了智能处理。

对于进入 NLP 评估领域的学生和研究人员来说，这篇论文是一个完美的例子，展示了如何借鉴其他领域 (如心理测量学) 的数学工具来解决现代 AI 问题。下次当你看到排行榜时，请记住: 这不仅关乎谁赢得了比赛，还关乎谁在观看比赛。