引言

在时间序列预测的世界里——无论是预测股价、医院入院率还是电力需求——知道将会发生什么仅仅是战斗的一半。另一半，往往也是更关键的一半，是知道我们对这一预测有多大把握。

想象一下人工智能在预测交通流量。预测“每分钟 50 辆车”是有用的。但预测“每分钟 50 辆车，误差在 5 辆以内”与“每分钟 50 辆车，误差可能达 40 辆”，这两种情况导致的决策截然不同。这就是概率时间序列预测的领域。

最近, 去噪扩散概率模型 (Denoising Diffusion Probabilistic Models, DDPMs) ——即 DALL-E 和 Stable Diffusion 等图像生成器背后的技术——在该领域展现出了惊人的潜力。它们非常擅长生成复杂的分布。然而，当应用于现实世界数据时，它们存在一个明显的缺陷: 通常假设数据中的“噪声” (不确定性) 是恒定的，或者遵循某种简单、固定的模式。

实际上，数据是非平稳的 (non-stationary) 。 股市在崩盘期间波动性会发生变化；流感病例的方差在爆发期间会爆炸式增长。标准的扩散模型很难适应这种不断变化的不确定性水平。

在这篇文章中，我们将深入探讨一篇新的研究论文: “Non-stationary Diffusion For Probabilistic Time Series Forecasting” (NsDiff) 。 我们将探索这一新颖的框架如何摒弃传统模型的僵化假设，使其能够动态适应现实世界中不断变化的混沌状态。

问题所在: 当物理学遇上统计学

为了理解为什么 NsDiff 是必要的，我们需要先看看扩散模型通常如何处理时间序列。

通用的预测方法是训练一个模型 \(f(\mathbf{X})\) 来预测未来的序列 \(\mathbf{Y}\)。这通常给出条件期望，即“平均”结果。为了获得概率分布 (即不确定性) ，扩散模型向数据中添加噪声，然后学习逆转这一过程。

大多数现有的 DDPM 依赖于加性噪声模型 (Additive Noise Model, ANM) 。 它们假设:

\[ \mathbf{Y} = f(\mathbf{X}) + \boldsymbol{\epsilon} \]

在这里，\(\boldsymbol{\epsilon}\) 代表平稳高斯噪声 \(\mathcal{N}(\mathbf{0}, \mathbf{I})\)。用通俗的话说，这个模型假设虽然趋势 (均值) 可能会根据输入 \(\mathbf{X}\) 而改变，但不确定性 (噪声的方差) 是固定且不变的。

视觉化展示其失效模式

这种假设在高风险场景中会失效。考虑预测患有类流感疾病 (ILI) 的患者数量。随着季节达到高峰，不仅患者数量增加，而且该数字的不可预测性也会增加。

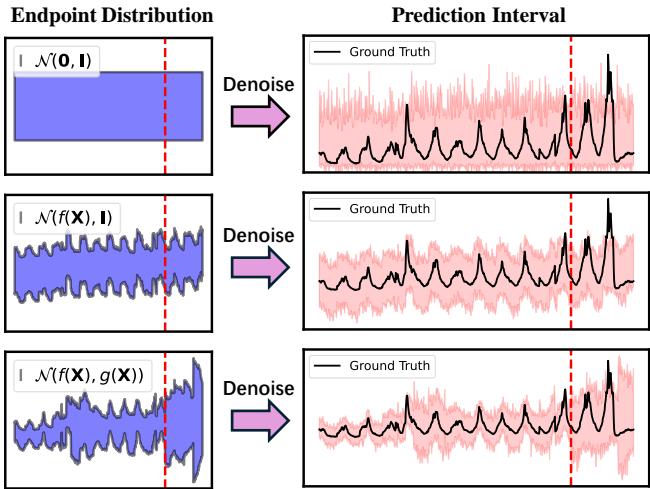
图 1 展示了使用不同终点训练的 DDPM，用于估算每周类流感疾病患者的数量。上图: 标准高斯分布。中图: 变化的均值。下图: 变化的均值和方差 (NsDiff) 。

上面的图 1 完美地说明了这一局限性:

  • 第一行 (TimeGrad): 该模型假设标准的均值为 0、方差为单位矩阵的高斯终点 \(\mathcal{N}(0, \mathbf{I})\)。注意右侧的预测区间 (粉色阴影区域) 是均匀的，未能捕捉到上升的趋势或扩大的不确定性。
  • 第二行 (TMDM): 该模型有所改进，目标是变化的均值 \(\mathcal{N}(f(\mathbf{X}), \mathbf{I})\)。它捕捉到了趋势 (曲线向上) ，但粉色区间的宽度保持不变。本质上，它认为在疫情高峰期的预测与开始时一样“安全”。
  • 第三行 (NsDiff - 本文重点): 该模型的目标是 \(\mathcal{N}(f(\mathbf{X}), g(\mathbf{X}))\)。它既捕捉到了上升的趋势，也捕捉到了扩大的不确定性。随着情况变得更加动荡，粉色区间也随之变宽。

核心方法: 非平稳扩散 (NsDiff)

研究人员提出了一种名为 NsDiff 的解决方案。其核心创新在于放宽了僵化的加性噪声模型，并将其替换为位置-尺度噪声模型 (Location-Scale Noise Model, LSNM) 。

1. 位置-尺度噪声模型 (LSNM)

NsDiff 不再添加固定的噪声，而是使用更灵活的方程来对未来序列进行建模:

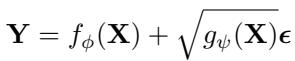
位置-尺度噪声模型的方程。

在这个方程中:

  • \(f_{\phi}(\mathbf{X})\) 对条件期望 (趋势) 进行建模。
  • \(g_{\psi}(\mathbf{X})\) 对变化的不确定性 (方差) 进行建模。
  • \(\epsilon\) 是标准高斯噪声。

通过引入 \(g_{\psi}(\mathbf{X})\)，模型承认噪声的“尺度”取决于输入数据 \(\mathbf{X}\)。如果输入暗示了一段动荡时期 (比如交通数据中的假期高峰) ，\(g_{\psi}(\mathbf{X})\) 就会变大。如果输入暗示了一段平静时期，它就会变小。

\(f_{\phi}\) 和 \(g_{\psi}\) 均由预训练的神经网络 (如 Transformer 或 MLP) 实现，为扩散过程提供“先验知识”。

2. NsDiff 框架

我们如何训练一个扩散模型来遵守这个新的噪声模型呢？作者设计了一个集成感知不确定性的噪声调度 (uncertainty-aware noise schedule) 的框架。

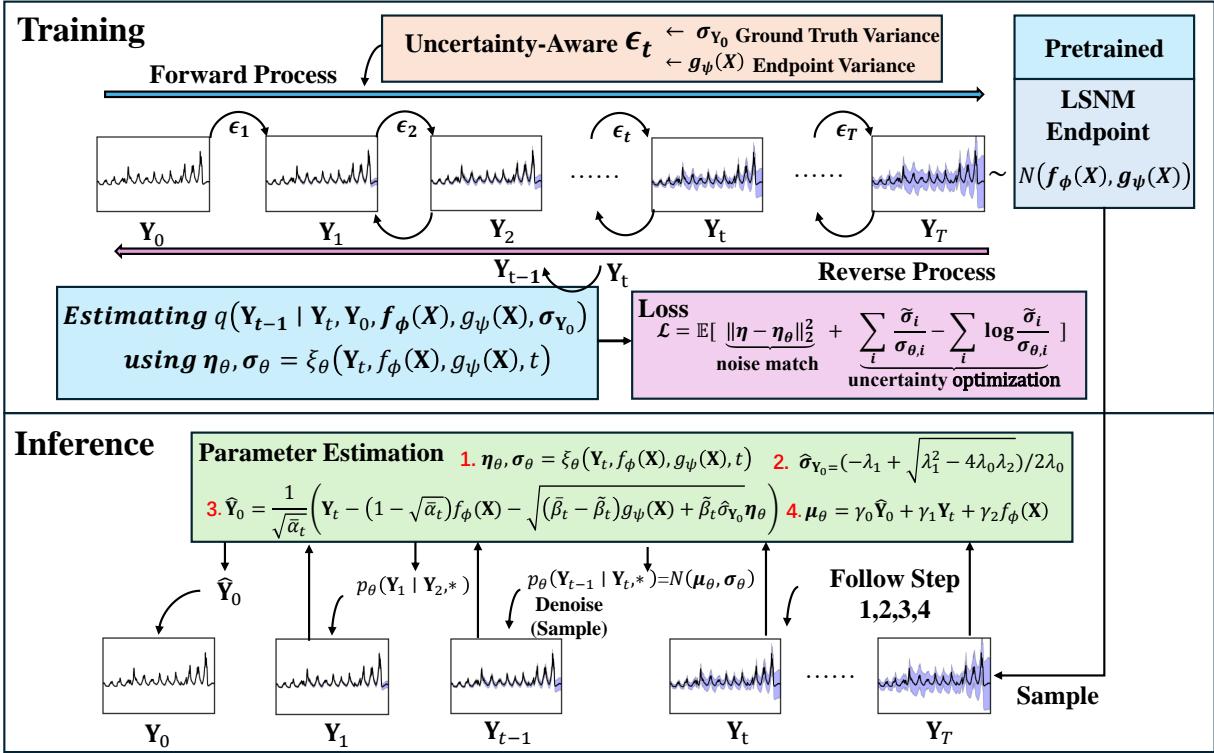
图 2. NsDiff 的概要。它集成了基于 LSNM 的终点和感知不确定性的噪声调度。

如图 2 所示，该过程涉及两个主要阶段:

  1. 训练 (Training - 顶部): 我们获取地面真值 \(\mathbf{Y}_0\) 并逐渐添加噪声，直到其达到目标分布 \(\mathbf{Y}_T\)。关键在于，与标准 DDPM 中 \(\mathbf{Y}_T\) 是随机噪声不同，这里的 \(\mathbf{Y}_T\) 来源于我们的先验 \(f_{\phi}(\mathbf{X})\) 和 \(g_{\psi}(\mathbf{X})\)。
  2. 推理 (Inference - 底部): 我们从预测的终点分布 (使用先验) 开始采样，并迭代去噪以生成最终预测。

3. 感知不确定性的噪声调度

这部分是数学上的精妙之处。在标准的扩散模型中，你会根据固定的调度 \(\beta_t\) 添加噪声。在 NsDiff 中，每一步添加的噪声必须考虑到我们正在移向一个特定的、依赖于数据的方差 \(g_{\psi}(\mathbf{X})\)。

前向过程分布 \(q(\mathbf{Y}_t | \mathbf{Y}_{t-1})\) 被修改了。任何步骤 \(t\) 的噪声数据分布计算如下:

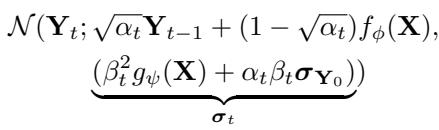
显示具有自适应方差 sigma_t 的前向过程正态分布的方程。

仔细观察上式中的方差项 \(\pmb{\sigma}_t\)。它是预测方差 \(g_{\psi}(\mathbf{X})\) 和实际数据方差 \(\sigma_{\mathbf{Y}_0}\) 的加权组合。

  • 当 \(t \to T\) (噪声更多) 时，方差收敛于我们估计的 \(g_{\psi}(\mathbf{X})\)。
  • 当 \(t \to 0\) (噪声更少) 时，它反映了实际数据。

这种动态调整允许扩散过程在干净数据和我们想要建模的复杂、非平稳终点之间架起“桥梁”。

4. 逆向过程与损失函数

逆向过程 (去噪) 的目标是估计被添加的噪声 \(\boldsymbol{\eta}\)。神经网络 \(\xi_{\theta}\) 接收噪声步骤 \(\mathbf{Y}_t\)、先验 \(f_{\phi}\) 和 \(g_{\psi}\) 以及时间步长 \(t\) 作为输入。

用于训练该网络的损失函数很有趣，因为它不仅仅关注噪声的误差；它还针对方差进行了优化:

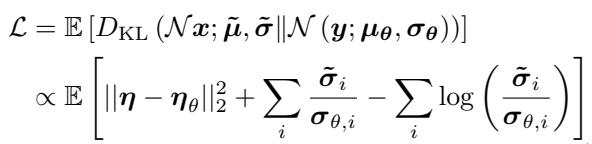
结合噪声匹配和不确定性优化的损失函数方程。

第一项 \(||\boldsymbol{\eta} - \boldsymbol{\eta}_{\theta}||^2\) 确保均值被正确估计 (DDPM 中的标准做法) 。右侧的求和项专门惩罚方差估计中的误差，迫使模型关注不确定性的尺度。

5. 推理: 二次方程解法

这里有一个引人入胜的技术细节。为了准确执行逆向去噪步骤，模型需要知道原始数据的方差 \(\sigma_{\mathbf{Y}_0}\)。

在训练期间，我们知道地面真值 \(\mathbf{Y}_0\)，所以计算其方差很简单。但在推理期间 (预测未来时) ，我们没有 \(\mathbf{Y}_0\)。

我们可以直接使用预测器 \(g_{\psi}(\mathbf{X})\)，但这相当于盲目信任预训练模型，而忽略了扩散模型在逆向过程中观察到的信息。相反，作者推导了估计的噪声方差 \(\sigma_{\theta}\) 与地面真值方差之间的关系。

结果表明，这种关系构成了一个一元二次方程:

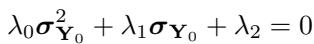
求解 sigma Y0 的二次方程。

通过求解这个关于 \(\sigma_{\mathbf{Y}_0}\) 的二次方程，模型可以在生成过程中动态估计目标数据的方差。

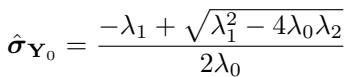
二次方程的解。

这使得 NsDiff 能够在生成样本时不断完善其对不确定性的理解，而不是仅仅依赖于预训练模型的初始猜测。

实验与结果

作者在九个真实世界数据集 (包括电力、交通和汇率) 以及旨在对不确定性处理进行压力测试的合成数据集上测试了 NsDiff。

真实世界表现

他们将 NsDiff 与 TimeGrad、CSDI 和 TMDM 等强基线模型进行了比较。使用的指标是 CRPS (连续概率排位分数——衡量分布的准确性) 和 QICE (分位数区间覆盖误差——衡量预测区间覆盖真实数据的程度) 。两个指标都是越低越好。

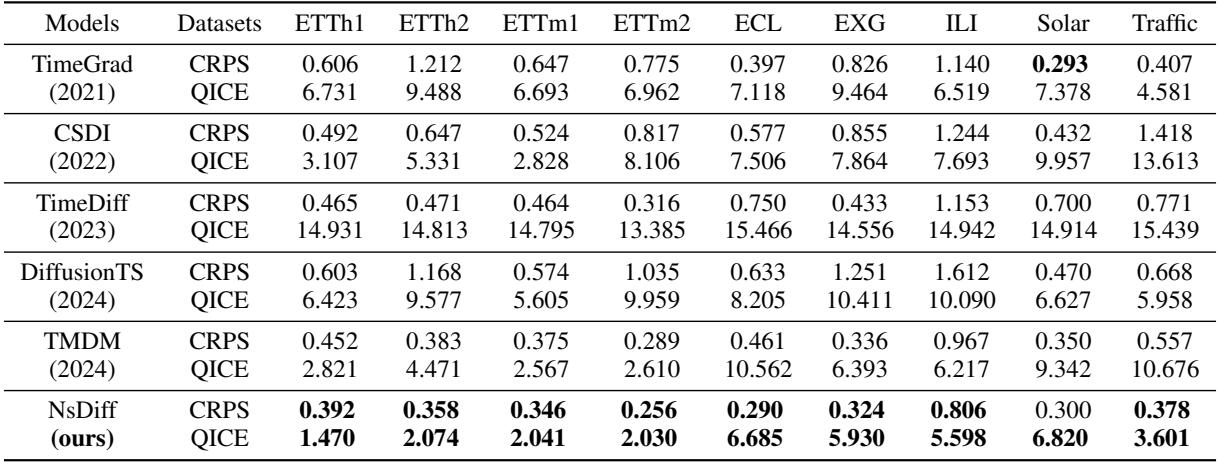
表 3. 九个真实世界数据集的实验结果。

如表 3 所示，NsDiff 在几乎所有数据集上都取得了最先进的结果。

  • 在Traffic (交通) 数据集上 (该数据集具有极高的不确定性变化) ，NsDiff 将 QICE 得分比 TMDM 降低了 66.3% 。
  • 在 ETTh1 和 ETTh2 (电力变压器数据) 上，它将 QICE 降低了大约 50% 。

视觉验证

数字固然重要，但时间序列预测需要眼见为实。让我们看看 ETTh1 数据集的一个样本。

图 3. ETTh1 模型间 95% 预测区间的比较。

在图 3 中:

  • TimeGrad 和 CSDI (右侧) 表现挣扎。TimeGrad 预测的是平坦的趋势，而实际上数据急剧下降。
  • TMDM (左数第二个) 捕捉到了均值的下降 (黑线) ，但请看粉色区间。它是一个宽度恒定的管状。它没有意识到下降可能会引入更多的波动。
  • NsDiff (左侧) 不仅捕捉到了下降，还提供了一个紧贴地面真值的紧密、准确的预测区间。

合成数据压力测试

为了严格证明 NsDiff 能更好地处理变化的方差，研究人员创建了合成数据集，其中的方差随时间线性或二次增长。

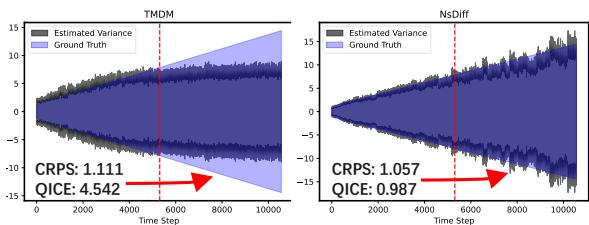
图 4. 线性方差数据集中的估计方差与地面真值。

图 4 是一个“确凿的证据”。

  • 左图 (TMDM) 显示该模型实际上在方差变化上“放弃了”。在红色虚线 (测试集) 之后，预测方差 (灰线) 变平，完全错过了地面真值方差 (蓝色阴影) 正在增加的事实。
  • 右图 (NsDiff) 几乎完美地追踪了增加的方差。它理解环境已经改变，并相应地调整了其不确定性估计。

结论与启示

NsDiff 论文强调了生成式时间序列预测中的一个关键缺陷: 对不确定性平稳性的假设。通过坚持使用加性噪声模型，以前的最先进模型本质上就像戴着眼罩，能看到趋势往哪里走，却对预测变得多么危险视而不见。

通过整合位置-尺度噪声模型 (LSNM) 并推导出数学上严谨的感知不确定性的噪声调度 , NsDiff 提供了一个通用的框架。它本质上是在说: “让我们利用扩散模型的力量，但让我们用关于均值和方差的明确、自适应的先验来引导它们。”

对于学生和从业者来说，这篇论文是关于归纳偏置 (inductive bias) 的一堂精彩课程。一个强大的通用模型 (如标准 DDPM) 往往会输给一个结合了特定问题结构知识 (如方差随时间变化这一事实) 的模型。随着我们迈向使用 AI 进行关键基础设施和金融决策，像 NsDiff 这样能够诚实且准确地报告自身不确定性的工具将是不可或缺的。