在人工智能飞速发展的格局中，一场新的、有些令人不安的猫鼠游戏正在浮现。我们依赖机器学习 (ML) 模型进行高风险决策——从批准贷款申请到调节社交媒体上的仇恨言论。因此，监管机构和整个社会都要求这些模型必须是“公平”的。它们不应基于性别、种族或年龄进行歧视。

但问题在于: 你如何验证一个黑盒模型是否公平?

通常，审计员会向模型发送一组测试查询并检查答案。但是，如果模型知道自己正在被测试呢？就像臭名昭著的“柴油门”丑闻中汽车检测到排放测试并改变其性能一样，AI 平台理论上可以检测到审计，并暂时切换到“公平”模式。这种做法被称为公平洗白 (fairwashing) 或审计操纵 。

在这篇深度文章中，我们将探讨一篇引人入胜的研究论文 《利用先验知识进行鲁棒的机器学习审计》 (Robust ML Auditing using Prior Knowledge) , 该论文提出了一个数学和实践框架来捕捉这些作弊模型。我们将逐步了解公平洗白是如何运作的，为什么标准审计会失败，以及利用“秘密”的先验知识如何帮助审计员不仅验证平台表面上是否看起来公平，而且验证其是否真正诚实。

问题所在: 黑盒审计的脆弱性

要理解解决方案，首先需要了解其脆弱性。大多数第三方审计都是“黑盒”审计。审计员看不到代码或训练数据；他们只能发送输入 (\(X\)) 并观察输出 (\(Y\)) 。

目前的法规通常要求审计员在审计前通知平台。这这就造成了一个巨大的漏洞。出于利润或运营效率的动机，平台可能会在日常用户服务中使用一个有偏见但准确度极高的模型。然而，一旦收到“审计集” (来自监管机构的问题列表) ，平台就可以无缝地切换其行为。

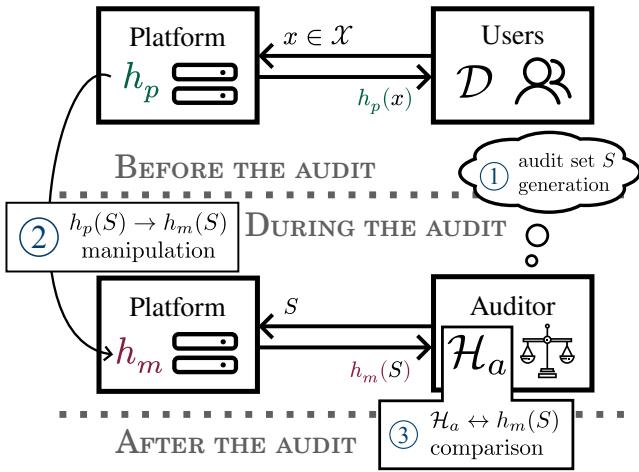
审计过程图解，显示了用户、平台和审计员之间的交互。

如图 1 所示，流程通常如下:

  1. 正常运行: 用户与平台的标准模型 \(h_p\) 交互。
  2. 审计: 审计员生成审计数据集 \(S\) 并将其发送给平台。
  3. 操纵: 平台收到 \(S\)。它不是用 \(h_p\) 诚实作答，而是计算出一组操纵后的答案 \(h_m\)，这些答案是专门为了在数据集 \(S\) 上看起来公平而设计的。
  4. 评估: 审计员分析操纵后的答案 \(h_m(S)\)。如果它们看起来公平，平台就会通过审计，即使它对待真实用户并不公平。

定义公平: 人口统计学均等

为了具体说明这一点，让我们定义审计员通常寻找的内容。最常见的指标之一是人口统计学均等 (Demographic Parity, DP) 。

人口统计学均等本质上要求不同群体 (例如男性与女性) 获得正面结果 (如获得贷款或帖子被批准) 的比率应该相同，而不管输入特征如何。

在数学上，指标 \(\mu(h)\) 代表两个群体 (其中 \(A=1\) 是一个群体，\(A=0\) 是另一个群体) 获得正面结果的概率差异:

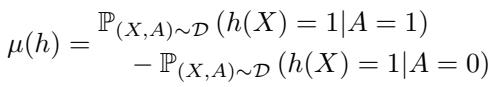
展示人口统计学均等公式的方程。

如果 \(\mu(h) = 0\)，则模型被认为是公平的。所有公平模型的集合表示为 \(\mathcal{F}\)。

问题在于 DP 极易被操纵。平台不需要重新训练庞大的神经网络来通过 DP 审计。它只需要在审计数据集 \(S\) 中将弱势群体的一些“否”决定的结果翻转为“是”，直到数字平衡为止。

解决方案: 利用先验知识进行审计

如果平台可以操纵其答案以表现得公平，那么仅仅检查公平性是不够的。审计员需要同时检查两件事:

  1. 平台公平吗? (\(h_m \in \mathcal{F}\))
  2. 平台诚实吗? 他们展示给我们的模型 (\(h_m\)) 对于这项任务来说，表现得像一个合理的模型吗？

第二个问题正是先验知识 (Prior Knowledge) 发挥作用的地方。审计员需要一个“审计员先验” (\(\mathcal{H}_a\)) ——即他们预期会看到的一组模型。

检查平台是否公平以及是否诚实的两个方程。

如果平台返回的模型 \(h_m\) 非常公平，但做出的预测极其离奇，没有任何理性的模型会这样做 (例如，仅仅为了平衡配额而将清晰的猫的图像分类为狗) ，审计员就应该将其标记为“不诚实”。

公共先验的陷阱

审计员的本能反应可能是使用公共数据来构建这种先验知识。例如，如果审计一个仇恨言论检测器，审计员可能会下载像“维基百科评论”这样的公共数据集，并检查平台的模型在其上的表现。

然而，研究人员证明了一个关于公共先验的毁灭性定理: 如果审计员使用公共知识，平台总是可以作弊。

定理: 如果平台知道审计员的先验 (\(\mathcal{H}_a\)) ，它只需找到一个位于“公平模型”和“可预期模型”交集 (\(\mathcal{H}_a \cap \mathcal{F}\)) 中的模型。

由于平台知道公共数据集，它可以确保其操纵后的答案在该公共数据集上实现高准确度，同时也满足公平性约束。对审计员来说，该模型看起来既公平又准确。平台赢了。

私有数据的力量

为了击败操纵，审计员必须拥有私有知识——具体来说，是一个平台从未见过且无法预测的带标签数据集 \(D_a\)。

利用这个私有数据集，审计员定义了“可预期模型集合” (\(\mathcal{H}_a\)) ，如下所示:

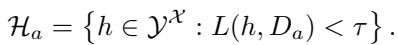
定义基于损失阈值 tau 的可预期模型集合 Ha 的方程。

简单来说: \(\mathcal{H}_a\) 包含所有在审计员的私有数据上错误率 (损失 \(L\)) 低于特定阈值 \(\tau\) 的模型。

如果平台发回的答案 (\(h_m\)) 在审计员的私有数据上错误率很高 (即损失大于 \(\tau\)) ，审计员就会知道有猫腻。平台可能为了伪造公平性而极度扭曲了其答案，以至于该模型在真实数据上不再合理。

几何直觉: 球体与平面

这一概念最好通过几何学来理解。想象所有可能的机器学习模型的空间。

  1. 公平平面 (\(\mathcal{F}\)) : 该空间中有一个特定的切片 (超平面) ，包含所有满足人口统计学均等的模型。
  2. 可预期球体 (\(\mathcal{H}_a\)) : 审计员的私有数据集定义了一个“球”或球体。这个球体内的任何模型都是“足够好”或“可预期”的，因为它在私有数据上的误差很低。

平台使用的诚实模型 \(h_p\) 很可能在可预期球体内部 (因为它是一个好模型) ，但不在公平平面上 (因为它有偏见) 。

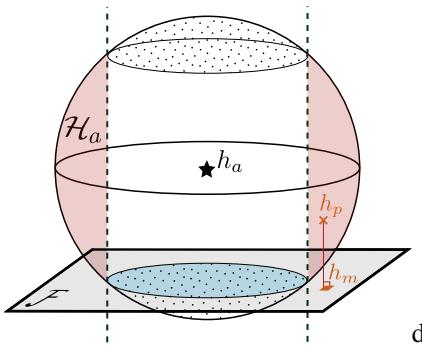
几何表示展示了诚实模型 hp、操纵后的模型 hm、审计员先验 Ha 和公平平面 F。

上方的图 2 形象地展示了这个陷阱。

  • \(h_p\) (诚实模型) : 它位于球体内部但偏离平面。
  • \(h_m\) (操纵后的模型) : 平台试图将 \(h_p\) 移动到蓝色的公平平面上。
  • 陷阱: 如果平台将 \(h_p\) 移至蓝色平面，但平面上的那个点落在了球体外部 (进入红色区域) ，审计员就会检测到操纵！该模型变得“不可预期” (误差太大) 。

平台希望落在蓝色阴影区域 (既公平又可预期) 。如果平台被迫进入红色区域 (公平但可疑) ，审计员就赢了。

最佳操纵的数学原理

平台并不是随机行事的。它希望以最小的撒谎代价通过审计。它想找到一个模型 \(h_m\)，既是公平的 (\(\in \mathcal{F}\)) ，又尽可能保持接近其原始行为 (\(h_p\)) ，以维持合理性。

这是一个优化问题。“最佳操纵”是诚实模型在公平平面上的数学投影 :

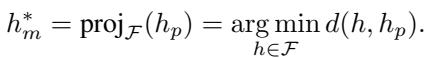
显示最佳操纵模型作为诚实模型在公平集合上的投影的方程。

平台计算出这个 \(h_m^*\) 发送给审计员。

审计员能抓住他们吗？

这篇论文的核心贡献是量化了捕捉这种最佳操纵的概率。这被称为检测率 (\(P_{uf}\)) 。

检测率取决于两个关键距离:

  1. \(\delta\) (Delta) : 地面真值 (Ground Truth) 的“不公平性”。实际可能的最佳模型距离公平平面有多远？如果现实世界本身非常有偏见 (高 \(\delta\)) ，诚实模型虽然在球体深处，但距离平面很远。
  2. \(\tau\) (Tau) : 审计员的容忍度。“可预期球体”有多大？\(\tau\) 大意味着审计员接受平庸的模型。\(\tau\) 小意味着审计员要求高准确度。

研究人员利用高维几何 (具体利用了沃利斯积分) 推导出了检测概率的闭式解。

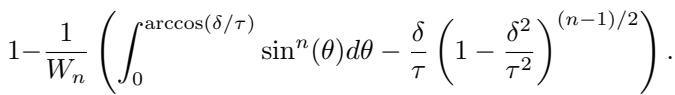
基于 n、delta 和 tau 计算检测概率的复杂方程。

虽然公式看起来令人生畏，但直觉很优雅。它计算的是球体与公平平面相交的“球冠”体积。如果该交集很小，平台安全落在其中的概率就很低。

该概率的一个简化下界为:

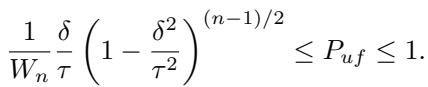
显示检测概率 Puf 下界和上界的不等式。

数学上的关键结论:

  • 如果 \(\tau \approx \delta\) (审计员非常严格，球体的半径仅略大于到公平平面的距离) ，检测概率趋近于 1。平台无处藏身。
  • 如果 \(\tau\) 很大 (审计员很宽容) ，检测概率下降。平台有足够的空间找到一个既公平又“足够好”的模型。

实验现实: 他们能隐藏多少？

理论是合理的，但在真实数据面前站得住脚吗？研究人员使用两个数据集测试了这个框架:

  1. CelebA: 一个名人面孔的计算机视觉数据集 (预测“微笑”或“高颧骨”等属性) 。
  2. ACSEmployment: 一个基于人口普查数据预测就业状态的表格数据集。

他们模拟了一个使用复杂操纵策略 (如“ROC 缓解”和“标签传输”) 来伪造公平性的平台。

“可隐藏的不公平性”概念

研究人员测量了可隐藏的不公平性 (Concealable Unfairness) : 平台在审计员注意到问题之前 (即检测分数超过阈值之前) 可以隐藏的最大偏见量。

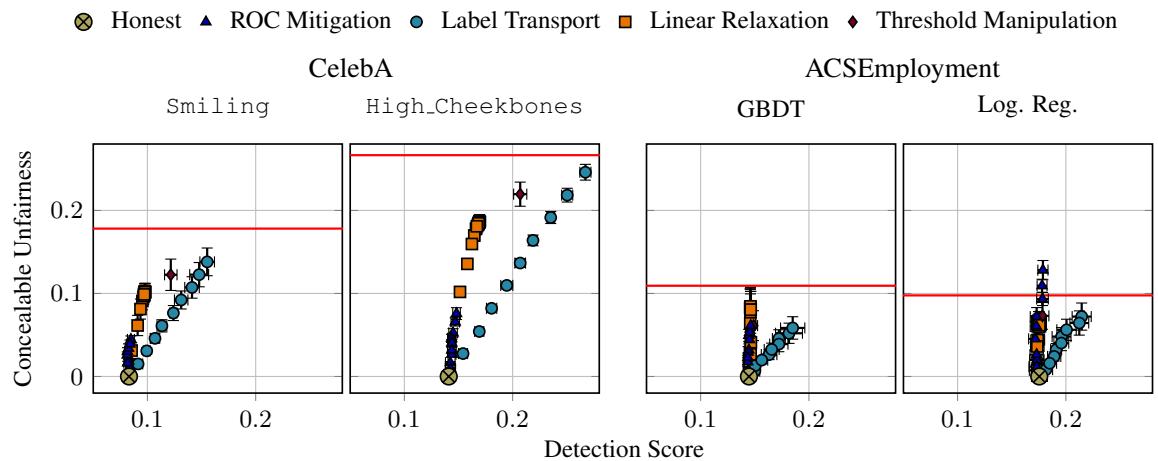
图表显示了不同数据集和方法的可隐藏不公平性与检测分数的关系。

图 3 显示了结果。

  • Y 轴是可隐藏的不公平性。
  • X 轴是检测分数 (审计员私有数据上的误差) 。
  • 红线代表原始、诚实模型的不公平性。

结论如何? 看看曲线升得有多高。对于大多数数据集，平台可以隐藏其所有的不公平性 (曲线触及红线) ，同时保持相对较低的检测分数。

例如，在“CelebA Smiling” (左上) 图中，平台可以在检测分数约为 0.13 时完全隐藏偏见。如果审计员将其阈值 \(\tau\) 设得高于 0.13，平台就能完全逃脱惩罚。

“审计预算”困境

人们可能会认为，只要审计员收集更多数据 (增加审计预算 \(n\)) ，他们最终就能抓住撒谎者。

研究人员通过将审计集规模从 100 个样本增加到 5,000 个样本来测试这一点。

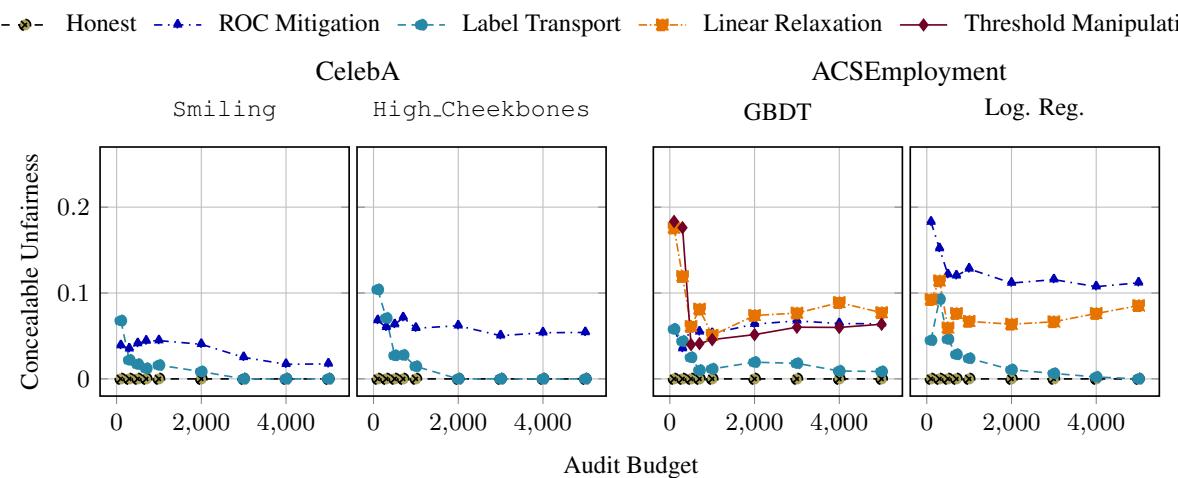
图表显示可隐藏不公平性与审计预算的关系。

图 4 揭示了一个令人惊讶的细微差别:

  • 左上 (CelebA Smiling) : 随着预算增加，可隐藏的不公平性降至零。这是成功的！任务很“简单” (低不确定性) ，因此审计员可以执行严格的阈值。
  • 右上 (CelebA High Cheekbones) : 曲线保持平坦。即使有 5,000 个样本，平台仍然可以隐藏显著的不公平性。

为什么? “高颧骨”任务更难。最先进的模型本来就有较高的错误率。这迫使审计员使用更宽松的阈值 \(\tau\) (以避免错误标记诚实但不完美的模型) 。这种宽松给了恶意平台操纵结果所需的“回旋余地”，无论审计员使用多少数据。

实施最佳操纵

值得注意的是平台是如何作弊的。论文指出了一个讽刺之处: 用于伪造公平性的技术，正是科学界开发出来用于修复公平性的技术。

平台解决了这个优化问题:

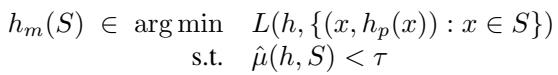
平台在确保公平性指标低于 tau 的同时最小化损失的优化问题。

他们使用诸如ROC 缓解 (ROC Mitigation) 或线性松弛 (Linear Relaxation) 等方法。在实验中，研究人员发现，当仅应用于审计集时，这些标准的“公平性修复”工具在欺骗审计员方面非常有效。

结论与关键要点

论文 《利用先验知识进行鲁棒的机器学习审计》 为 AI 治理敲响了警钟。它表明，天真的黑盒审计在根本上是有缺陷的。如果平台知道自己正在被审计，它几乎总是可以操纵结果以表现得公平。

以下是给学生和未来从业者的关键要点:

  1. 公共基准对审计是不安全的: 如果先验知识是公开的，平台就可以利用它。定理 3.2 证明这是一条死胡同。
  2. 私有数据至关重要: 审计员必须维护秘密的、高质量的标记数据集 (\(D_a\)) 来验证平台的诚实性。
  3. 不确定性的“回旋余地”: 机器学习任务越难，审计就越难。如果任务具有很高的自然错误率，审计员必须宽容，这不可避免地允许平台隐藏偏见。
  4. 几何学很重要: 理解“公平平面”和“模型假设球体”之间的几何关系，使我们能够从数学上计算捕捉作弊者的概率。

随着我们迈向一个实施 AI 法规 (如欧盟 AI 法案) 的世界，这项研究强调了审计不仅仅是一个官僚主义的勾选框。这是一场对抗性博弈。为了确保 AI 有益无害，审计员需要像他们监督的模型一样复杂——并且配备同样丰富的数据。