引言

想象一下，你拿到了一张包含两列数据的电子表格: A 列和 B 列。你将它们绘制出来，发现它们完全相关。随着 A 列数值增加，B 列数值也随之增加。

现在，请回答这个问题: 是 A 导致了 B，还是 B 导致了 A?

这是科学、经济学和人工智能领域最基本的挑战之一。我们都听过这句口头禅“相关性不等于因果性”。通常，为了弄清因果方向，我们依赖于干预手段——我们会戳一下系统 (比如医学中的随机对照试验) 看看哪里会出问题。

但是，如果你不能干预系统呢？如果你只有观测数据，比如历史股价或来自遥远星系的望远镜读数呢？

在论文 《Identifying Causal Direction via Variational Bayesian Compression》 (通过变分贝叶斯压缩识别因果方向) 中，研究人员 Quang-Duy Tran 及其同事提出了一个引人入胜的解决方案，将深度学习、信息论和统计学联系在了一起。他们认为，“真正”的因果方向就是那个能最有效地压缩数据的方向。

为了实现这一目标，他们引入了一种称为 COMIC (COmpression-based method for Identifying Causal direction，基于压缩的因果方向识别方法) 的方法。通过使用贝叶斯神经网络来建模变量之间的关系，他们计算出哪个因果方向能最简洁地描述数据。

在这篇文章中，我们将拆解这篇论文，以理解为什么“简单”意味着因果关系，我们如何衡量神经网络的复杂性，以及为什么这种新方法优于传统的统计方法。

背景: 压缩的哲学

要理解计算机如何仅凭数字就能确定是下雨导致了草地变湿 (而不是反过来) ，我们需要了解 柯尔莫哥洛夫复杂性 (Kolmogorov Complexity) 的概念。

算法马尔可夫条件

这里的基本思想是奥卡姆剃刀: 最简单的解释通常是正确的。在信息论中，这被形式化为柯尔莫哥洛夫复杂性，即生成特定数据集所需的最短计算机程序的长度。

研究人员将其工作建立在 算法马尔可夫条件 (Algorithmic Markov Condition) 之上。该假设指出，如果 \(X\) 导致 \(Y\) (记为 \(X \to Y\)) ，那么生成 \(X\) 的机制和从 \(X\) 生成 \(Y\) 的机制是自然界中独立的“模块”。

如果我们试图描述这两个变量的联合分布 \(P(X, Y)\)，真正的因果方向会产生最有效的因式分解。

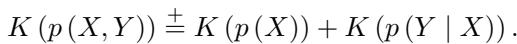
通过因式分解计算联合分布的柯尔莫哥洛夫复杂性。

在上面的公式中，\(K(\cdot)\) 代表复杂性 (或描述长度) 。该公式表明，对 \((X, Y)\) 这一对变量的复杂性大致等于原因 \(X\) 的复杂性加上在给定原因的情况下结果 \(Y\) 的复杂性。

关键点在于: 这种关系是不对称的。

如果 \(X \to Y\) 是真实方向，那么该方向的因式分解是“干净”的。然而，如果我们试图在反因果方向 (\(Y \to X\)) 上进行因式分解，\(P(Y)\) 和 \(P(X|Y)\) 这两项放在一起描述要比分开描述更简单，因为它们共享信息。宇宙不是先产生结果的；如果你强迫模型这样认为，数学描述就会变得混乱和臃肿。

因此，我们可以通过检查哪个方向产生的描述更短来测试因果关系:

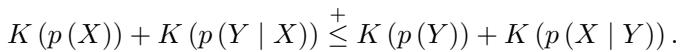
显示真实因果方向产生较低复杂性的不等式。

如果不等式左边较小，则 \(X\) 导致 \(Y\)。如果右边较小，则 \(Y\) 导致 \(X\)。

“理想”简单的难题

这里有个问题。柯尔莫哥洛夫复杂性在理论上是可计算的，但在实践中是不可能的。由于停机问题，你无法计算任意数据的“绝对最短程序”。

因此，研究人员依赖 最小描述长度 (MDL) 原则。我们不寻找完美的程序，而是试图从特定的模型类中找到最好的模型。我们计算传输数据所需的“码长” (或文件大小) 。

在 MDL 中，总码长由两部分组成:

  1. 模型成本 (\(L_2\)) : 描述模型的参数需要多少比特？
  2. 数据成本 (\(L_1\)) : 模型的拟合程度如何？ (如果模型拟合完美，“误差”残差很小，编码成本低。如果模型拟合很差，误差很大，编码成本高。)

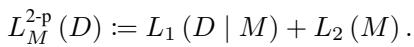
两部分 MDL 代码定义。

这产生了一个权衡。你可以用一个超级复杂的模型完美拟合数据 (高模型成本，低数据成本) ，或者用一个简单的模型但拟合较差 (低模型成本，高数据成本) 。“真正”的因果方向是使这两者之和最小化的方向。

为什么以前的方法失败了

在这篇论文之前，研究人员使用简单的回归模型 (如线性回归) 来估计这些码长。但现实世界并不是线性的。如果 \(X\) 和 \(Y\) 之间的关系是复杂的正弦波或锯齿状多项式，简单的模型无法捕捉到拟合，导致码长不准确。

其他人尝试了高斯过程 (GPs) ，它很灵活，但在计算上极其昂贵 (\(O(N^3)\)) ，这使得它们对大数据集毫无用处。

这引出了作者的提议: 神经网络。

核心方法: COMIC

本文介绍的方法是 COMIC 。 它代表基于贝叶斯压缩的因果方向识别方法 (Bayesian COMpression-based approach to Identifying the Causal direction) 。

作者建议使用神经网络，因为它们是“通用近似器”——它们可以模拟任何关系，无论是线性的还是非线性的。然而，标准神经网络容易过拟合。如果你使用一个巨大的网络，它会记住数据。它的“数据成本” (误差) 将为零，但它的“模型成本” (复杂性) 理论上应该是巨大的。

问题在于，在标准深度学习中，我们通常不测量权重的“文件大小”。我们只是最小化误差。

为了解决这个问题，作者利用了 变分贝叶斯 (VB) 学习 。

变分贝叶斯编码

如何计算神经网络的文件大小？你不再把权重视为固定的数字，而是视为概率分布。

在贝叶斯神经网络中，每个权重 \(w\) 都是由均值 \(\mu\) 和方差 \(\sigma^2\) 定义的钟形曲线 (高斯分布) 。

  • 如果方差很小，权重就很精确 (需要更多信息/比特来编码) 。
  • 如果方差很大，权重就很模糊 (需要较少比特) 。

作者使用了一种称为 Bits-Back 编码 的编码方案 (概念上类似于变分证据下界或 ELBO) 。条件分布 \(Y|X\) 的总码长通过最小化以下目标函数来近似:

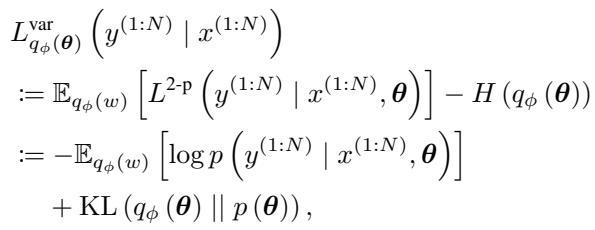
变分贝叶斯目标函数 (ELBO)。

让我们分解这个关键方程:

  1. 第一项 (数据拟合度) : \(-\mathbb{E}[\log p(y|x, \theta)]\)。这衡量了网络在给定 \(X\) 的情况下预测 \(Y\) 的能力。它本质上是在看数据的似然性。如果预测得好，这个数字就很低。
  2. 第二项 (模型复杂性) : \(KL(q_\phi(\theta) || p(\theta))\)。这是 Kullback-Leibler 散度 。 它衡量了学习到的权重后验分布 \(q_\phi\) 与简单的先验分布 \(p(\theta)\) (通常是标准高斯分布) 之间的“距离”。

可以将先验 \(p(\theta)\) 想象为模型的“默认”状态 (随机噪声) 。KL 项衡量了模型为了拟合数据而必须从随机状态移动多少“信息量”。 这有效地计算了以比特 (或纳特) 为单位的模型复杂性 (\(L_2\)) 。

原因的架构

COMIC 通过比较两个模型来确定方向:

  1. 正向模型: 假设 \(X\) 导致 \(Y\)。
  • 使用标准边缘分布编码 \(X\) (成本 = \(L_{marginal}(X)\)) 。
  • 训练一个贝叶斯神经网络从 \(X\) 预测 \(Y\)。
  • 计算 VB 码长 (成本 = \(L_{conditional}(Y|X)\)) 。
  1. 反向模型: 假设 \(Y\) 导致 \(X\)。
  • 使用标准边缘分布编码 \(Y\)。
  • 训练一个贝叶斯神经网络从 \(Y\) 预测 \(X\)。
  • 计算 VB 码长。

\(X \to Y\) 方向的总得分是边缘部分和条件部分的总和:

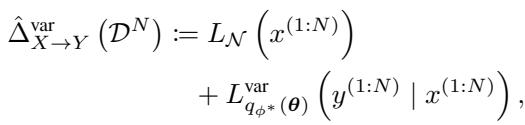
X 到 Y 的总估计码长。

神经网络本身不仅仅是一个标准的回归器。它模拟了 异方差性 (Heteroscedasticity) (变化的噪声) 。在因果发现中，“噪声”或“误差”通常随输入值的不同而变化。为了捕捉这一点，网络对每个输入输出两个值: 预测均值 (\(\mu\)) 和预测噪声方差 (\(\sigma\)) 。

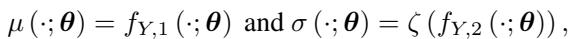
网络输出定义。

在这里，\(f_{Y,1}\) 预测 \(Y\) 的值，而 \(f_{Y,2}\) 预测该预测的不确定性 (标准差) 。\(\zeta\) 是一个确保方差始终为正的函数 (如 Softplus 函数) 。

因果指标得分

一旦模型在两个方向上都训练好了，我们只需比较得分。作者定义了因果指标 \(\hat{\Delta}^{\text{var}}\):

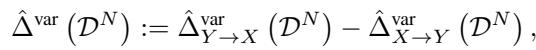
差值得分定义。

  • 如果 \(\hat{\Delta}^{\text{var}}\) 为 正，意味着 \(X \to Y\) 的码长更小 (更好) 。我们要得出的结论是 \(X\) 导致 \(Y\) 。
  • 如果 \(\hat{\Delta}^{\text{var}}\) 为 负，意味着 \(Y \to X\) 的码长更小。我们要得出的结论是 \(Y\) 导致 \(X\) 。
  • 数字的大小告诉我们置信度。接近零的结果意味着该方法“无法判定”。

为什么这是可识别的

这篇论文的主要理论贡献之一是证明了 可识别性 。

在许多统计模型 (如线性高斯模型) 中，两个方向的数学运算结果完全相同——你无法区分。这被称为“分布等价”。

作者证明了他们的特定设置 (具有高斯先验的贝叶斯神经网络) 是 不可分兼容的 (non-separable-compatible) 。

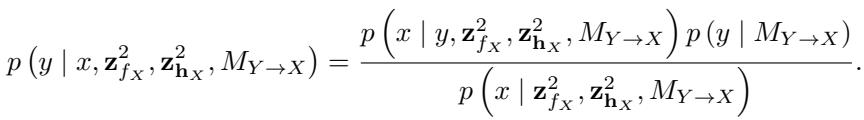
边缘似然因式分解。

如果不陷入繁琐的证明细节，其要点是: 如果你用神经网络在正向 (\(X \to Y\)) 生成数据，然后试图在反向 (\(Y \to X\)) 对其进行建模，反向模型产生的结果分布不属于同一个“简单”的分布族。反向方向上权重的先验会以复杂的方式依赖于数据分布。

这种不对称性保证了——只要有足够的数据——贝叶斯得分对于正确和错误的方向将是不同的。

实验与结果

理论固然好，但它行得通吗？作者将 COMIC 与一系列最先进的因果发现算法进行了测试。

竞争对手:

  • 基于 FCM 的方法: 试图拟合函数 \(Y = f(X) + Noise\) 并分析噪声。 (例如 CAM, LOCI) 。
  • 信息论方法: 像 COMIC 一样，这些方法寻找复杂性/熵模式。 (例如 SLOPE, RECI/SLOPPY, IGCI) 。
  • 高斯过程方法: GPLVM (COMIC 的近亲，但使用 GP 而不是神经网络) 。

基准测试: 测试使用了合成数据 (我们知道基本事实) 和真实世界数据 (图宾根因果对) 。

性能分析

结果使用 准确率 (Accuracy) (方向对了吗？) 和 Bi-AUROC (受试者工作特征曲线下的双向面积——二元分类性能的稳健度量) 进行评估。

让我们看看结果概览:

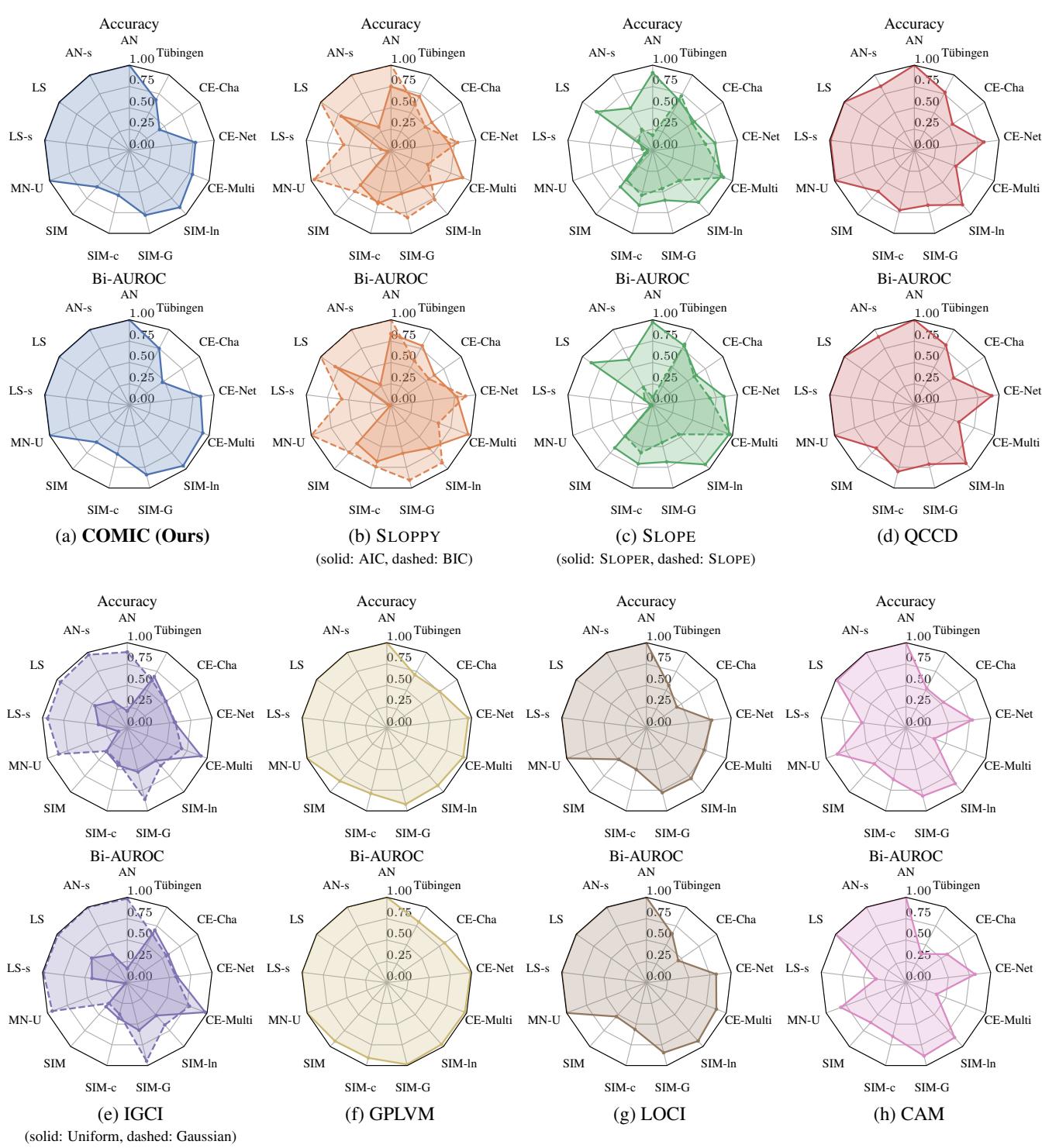
比较模型性能的雷达图。

解读雷达图 (图 1) :

  • 每个辐条代表不同的数据集 (AN, LS, MN-U 是合成的；Tübingen 是真实的) 。
  • 彩色多边形向外延伸得越远，性能越好。
  • 图 (a) 是 COMIC。 注意多边形有多“饱满”。它在几乎所有数据集上都达到了高准确率。
  • 对比 图 (h) CAM 。 CAM 在“AN” (加性噪声) 数据集上表现良好，因为它是为此设计的。但看看“CE-Multi”或“Tübingen”——它崩溃了。它太僵化了。
  • 对比 图 (d) QCCD 。 它表现良好，但与 COMIC 相比，在复杂的“CE-Multi”数据集上表现吃力。

总体汇总结果:

下面的条形图总结了所有数据集的平均性能。

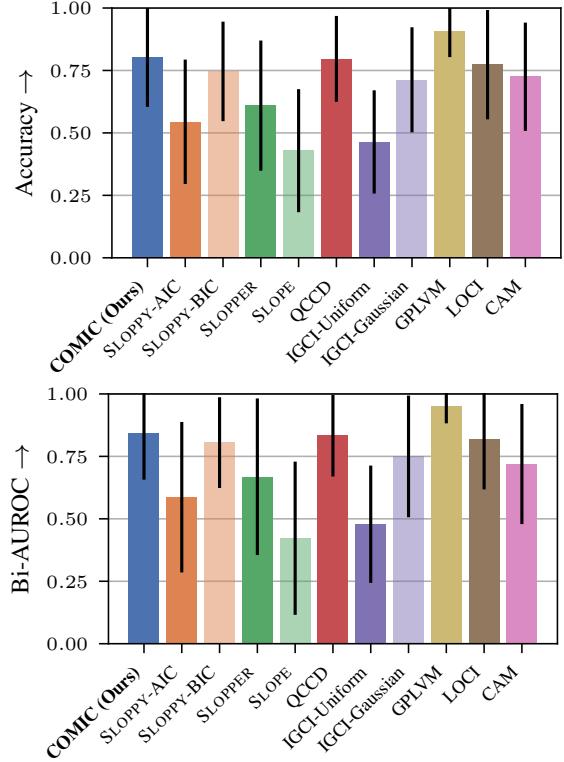
准确率和 Bi-AUROC 的条形图摘要。

数据中的关键结论:

  • COMIC vs. 最大似然 (LOCI/CAM): COMIC 优于最大似然方法 (右下角的绿色/橙色条) 。这验证了假设: 仅拟合好数据是不够的；必须惩罚复杂性。最大似然方法会对“错误”方向过拟合，使其看起来看似合理。
  • COMIC vs. GPLVM: 高斯过程方法 (GPLVM) 是唯一在某些指标上与 COMIC 匹敌或略胜一筹的竞争对手。然而，作者指出了一个关键的实际差异: GPLVM 计算量大，需要 GPU 和大量时间。COMIC 使用高效的神经网络反向传播，在性能和可扩展性之间取得了平衡。
  • 真实世界性能: 在图宾根数据集 (真实数据) 上，COMIC 取得了与大多数基于复杂性的方法相当或更好的准确率。这一点至关重要，因为真实世界的数据很少遵循合成数据那样清晰的数学规则。

鲁棒性

作者还进行了“消融实验” (测试模型的哪些部分重要) 。

  • 网络宽度: 他们发现，如果神经网络太宽 (例如，对于简单的变量对使用 200 个隐藏神经元) ，变分推断开始忽略数据 (后验塌陷为先验) 。中等宽度 (10-50 个神经元) 效果最好。
  • 先验: 对权重的方差使用均匀超先验比简单的固定先验效果更好。

结论与启示

论文 《Identifying Causal Direction via Variational Bayesian Compression》 为因果发现工具箱提供了一个引人注目的新工具。

通过将 因果关系 等同于 可压缩性 , 作者利用现代深度学习的巨大力量解决了困扰统计学家一个世纪的问题。COMIC 方法将神经网络的描述长度视为自然机制复杂性的代理。

为什么这很重要?

  1. 灵活性: 与之前假设线性关系或特定噪声类型的方法不同，COMIC 使用神经网络，使其能够适应生物学和金融学中发现的复杂、非线性、异方差关系。
  2. 有原则的复杂性: 它解决了这种背景下神经网络的“黑盒”问题。我们不仅仅是看测试误差；我们正在通过变分推断测量网络本身的信息内容。
  3. 可扩展性: 它提供了一条比高斯过程更具可扩展性的因果发现路径。

虽然目前的版本专注于二元情况 (只有两个变量) ，但作者建议其基本原理——变分贝叶斯压缩——可以扩展到多元网络。这为发现大型系统中的复杂因果图打开了大门，可能有助于我们解开从基因组学到气候科学等领域中错综复杂的因果网络。

在寻找时间之箭的过程中，事实证明，最好的地图可能就是那个占用空间最小的地图。