简介

想象一下二维平面上漂浮着两团点云: 一团是红色的，另一团是蓝色的。你的任务是将每一个红点与一个蓝点配对，使得所有配对点之间的距离总和最小。这就是欧几里得双色匹配问题 (Euclidean Bi-Chromatic Matching problem) 。

虽然这听起来像是一个纯粹的几何谜题，但它实际上是 1-Wasserstein 距离 (也称为推土机距离，Earth Mover’s Distance) 的计算核心。这种度量标准在现代计算机科学中无处不在，从机器学习中比较概率分布 (如在 WGAN 中) ，到分析时间序列数据中的漂移，再到计算机视觉中的图像比较。

历史上，对于静态设置 (即点不移动的情况) ，我们要么有很好的算法来解决它。但是，如果数据是活的呢？如果点不断地出现和消失呢？在这种动态设置中，每次变更后重新运行静态算法极其缓慢。直到现在，最好的动态方法处理单个更新仍然需要线性时间——\(O(n)\)。如果你有数百万个数据点，这个等待时间简直太长了。

在最近的一篇论文中，研究人员展示了一个巨大的飞跃: 第一个具有次线性更新时间的完全动态算法 。 具体来说，对于任意小的参数 \(\varepsilon\)，他们的方法能在 \(O(n^\varepsilon)\) 时间内处理更新，同时保持一个近似比为 \(O(1/\varepsilon)\) 的解。

在这篇文章中，我们将拆解这个复杂的算法，理解它是如何实现如此高速度的。我们将了解它如何利用基于网格的层次结构，如何“隐式”地移动点，以及如何在数据变化时避免重复劳动。

问题: 测量分布之间的距离

在深入解决方案之前，让我们先形式化这个问题。给定 \(\mathbb{R}^2\) 中的一个集合 \(A\) (红点) 和一个集合 \(B\) (蓝点) 。假设 \(|A| = |B| = n\)。我们想要找到一个双射 (完美匹配) \(\mu: A \rightarrow B\)，使总欧几里得距离最小化。

这个问题等价于计算两个离散测度之间的 1-Wasserstein 距离，形式化定义为:

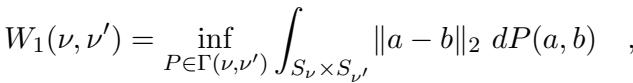
在动态场景中，我们会接收到一系列更新流。一个更新可能会插入一个新的红点和一个新的蓝点，或者删除现有的一对点。我们的目标是维护一个总成本较低的有效匹配，而无需每次都从头开始计算整个匹配。

核心方法

研究人员的方法建立在使用空间分解的“分治”策略之上。然而，他们以两种巧妙的方式对标准技术进行了改良: 他们使用了自底向上的构建方式 (从通过小单元格构建到大单元格) ，并且他们使用隐式匹配 (implicit matchings) 来处理数据，而无需遍历每一个点。

1. 分层网格 (p-树)

该算法的基础是一个称为受限 p-树 (restricted p-tree) 的数据结构。可以把它看作是增强版的四叉树 (Quadtree)。

在标准的四叉树中，一个正方形单元格被划分为 4 个较小的正方形。在 p-树中，边长为 \(L\) 的单元格被划分为 \(p \times p\) 的子网格 (其中 \(p\) 是一个参数，通常是 2 的幂，如 \(n^\varepsilon\)) 。这增加了分支因子，使树变得更浅，这对速度至关重要。

算法在开始时会随机偏移整个坐标系。这是几何算法中的一个标准技巧，目的是确保在极大概率下，最优匹配中的短边不会被大网格单元的边界“切断”。

2. 自底向上的匹配与“剩余点”

该算法从叶子节点 (最小的网格单元) 到根节点构建匹配。以下是树中单个节点 \(v\) 的直观逻辑:

1. 局部匹配: 查看严格位于此单元格内的所有红点和蓝点。
2. 贪心配对: 如果单元格包含 (比如) 10 个红点和 8 个蓝点，我们知道可以在此单元格内立即匹配 8 对。虽然我们还不知道确切是哪 8 对，但我们知道 8 个蓝点会抵消 8 个红点。
3. 转发剩余点: 剩下的 2 个红点在这里无法匹配。它们是“剩余点” (excess)。我们将这 2 个红点向上传递给父节点。父节点将尝试把它们与来自不同子单元格的剩余蓝点进行匹配。

这个过程确保了点尽可能在局部进行匹配。短边被优先考虑，因为只有当点在它们当前较小的邻域中绝对找不到伙伴时，才会被发送到父节点 (代表更大的空间区域) 。

3. 隐式匹配: 速度的关键

如果我们显式地存储和处理树每一层的每一个点，算法将会很慢。传递给根节点的“剩余”集合大小可能达到 \(O(n)\)，导致线性时间复杂度。

研究人员通过使用隐式匹配 (Implicit Matchings) 解决了这个问题。

算法不再将剩余点的确切坐标传递给父节点，而是将它们聚合。如果一个子单元格有剩余的红点，父节点会将它们视为位于该子单元格的中心 。

在父节点 \(v\) 内部，我们有一个子单元格网格。一些子单元格有剩余的红点，一些有剩余的蓝点。算法在这些子单元格的中心之间解决一个几何运输问题 (Geometric Transportation Problem) (一种广义的匹配问题) 。

让我们用论文中的一张图来可视化这一点:

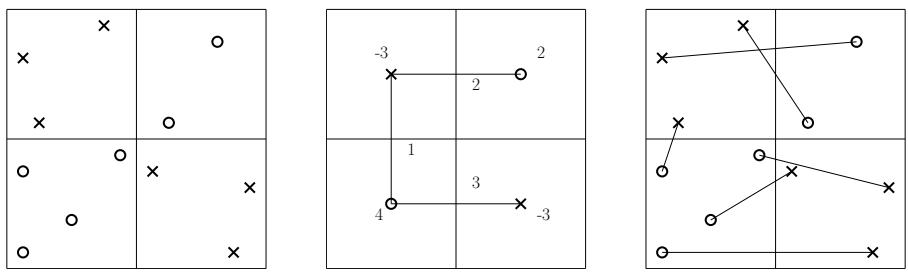
• 左图: 网格中的实际输入点。
• 中图: 隐式匹配 。 点被“对齐”到它们单元格的中心。数字代表供给 (红色) 和需求 (蓝色) 。边显示了多少“流” (匹配量) 在单元格中心之间移动。计算这个要快得多，因为无论内部有多少实际点，这里只有 \(p^2\) 个单元格中心。
• 右图: 显式匹配 。 中心之间的流被转换回真实点之间的具体边。

通过在“聚合”实例 (中图) 上解决问题，算法得到的解决方案成本非常接近真实点上的最优匹配成本，但其计算时间取决于 \(p\) (网格大小) ，而不是 \(n\) (总点数) 。

4. 动态化

那么，这种结构如何在次线性时间内处理更新呢？

当插入一个新点 \(x\) 时:

1. 叶子更新: 该点落入且仅落入一个叶子单元格。该叶子的局部匹配可能会改变。
2. 路径通向根节点: 这种变化可能会产生一个新的“剩余”点，被传递给父节点。父节点更新其隐式匹配 (单元格中心之间的运输问题) 。这可能会改变传递给它的父节点的剩余点，依此类推。
3. 受限范围: 关键在于，这种连锁反应仅沿着从叶子到根的路径向上传播。由于树很浅 (深度约为 \(1/\varepsilon\)) ，且每个节点的工作量取决于 \(p\) (即 \(n^\varepsilon\)) ，因此总更新时间约为 \(O(n^\varepsilon)\)。

算法不需要查看整个数据集。它只修复由沿着树的一条分支上的新点造成的“破坏”。

近似保证

你可能会问: 通过将点对齐到网格中心并贪婪地匹配它们，我们不会损失精度吗？

是的，严格来说，这是一种近似算法。我们牺牲了精确性以换取速度。然而，研究人员证明了误差是有界的。具体来说，算法生成的匹配 \(\mu_a\) 的期望成本与最优成本 \(c(\mu^*)\) 之间存在以下关系:

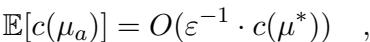
该等式表明成本至多是最优成本的 \(O(1/\varepsilon)\) 倍。如果你想要更紧密的近似 (更小的 \(\varepsilon\)) ，树会变得更深，网格会变得更细，这会增加运行时间。这是一个经典的权衡。

实验结果

理论听起来很可靠，但在实践中表现如何呢？作者使用合成数据 (均匀分布、高斯分布) 和真实世界数据 (纽约出租车行程) 将他们的实现与标准基线进行了测试。

加速比 vs. 静态算法

这项工作的主要动力是速度。下图显示了“加速因子”——即动态算法相对于从头重新运行静态近似算法快了多少倍。

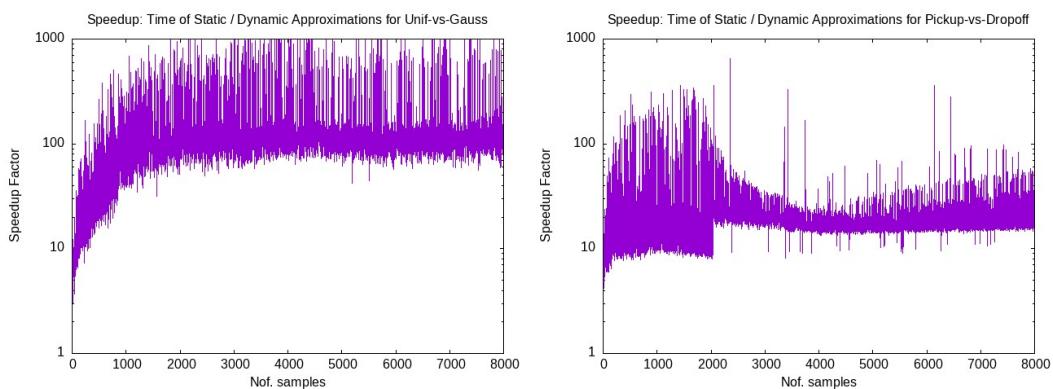
结果非常显著。动态算法快了几个数量级 (注意是对数刻度) 。随着数据集规模的增长 (X 轴) ，差距进一步扩大。对于需要实时响应的应用，静态重新计算根本不可行。

收敛性与可扩展性

同样重要的是验证算法随着样本量的增加是否真正收敛到正确的 Wasserstein 距离，以及更新时间是否保持在较低水平。

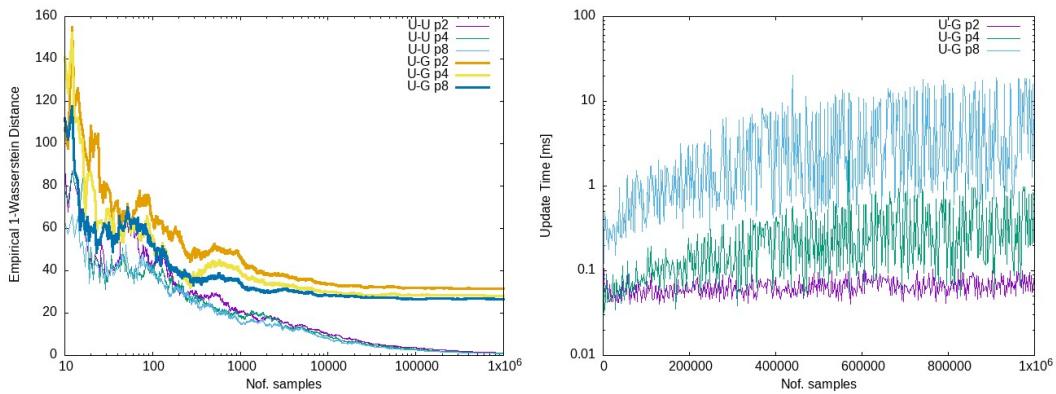
• 左图: 显示了估计的 Wasserstein 距离。注意近似曲线 (紫色、青色、绿色) 是如何紧跟精确解曲线的。
• 右图: 显示了以纳秒/毫秒为单位的更新时间。即使样本数量增长到 \(10^6\)，更新时间仍然极低 (通常在微秒或毫秒范围内) ，证实了次线性行为。

真实世界应用: 出租车数据

为了模拟真实世界的场景，研究人员使用了纽约出租车数据，将上车地点视为红点，下车地点视为蓝点。他们使用滑动窗口来模拟进入和离开系统的点。

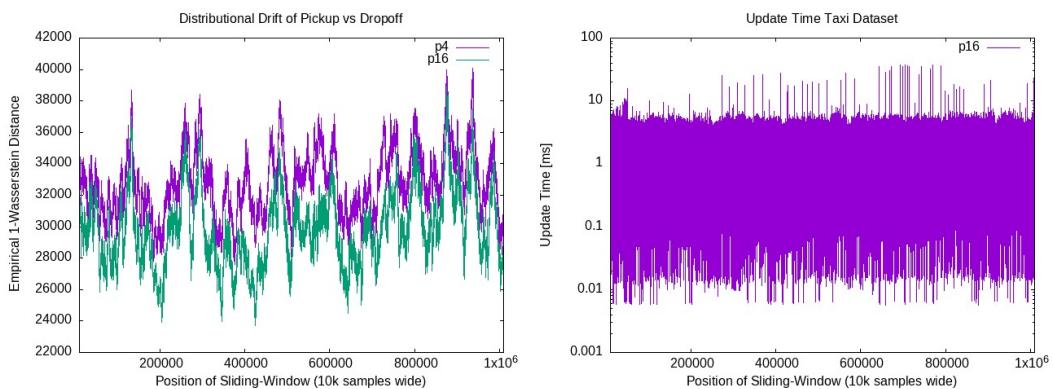
左图显示算法随时间跟踪“漂移” (分布的变化) 。随着城市交通模式的变化，估计的距离也会波动。 右图显示更新时间在整个模拟过程中保持稳定且处于低位。这证明了该算法在监控实时数据流方面的可行性。

准确性比较

最后，让我们看看近似解与精确解有多接近。

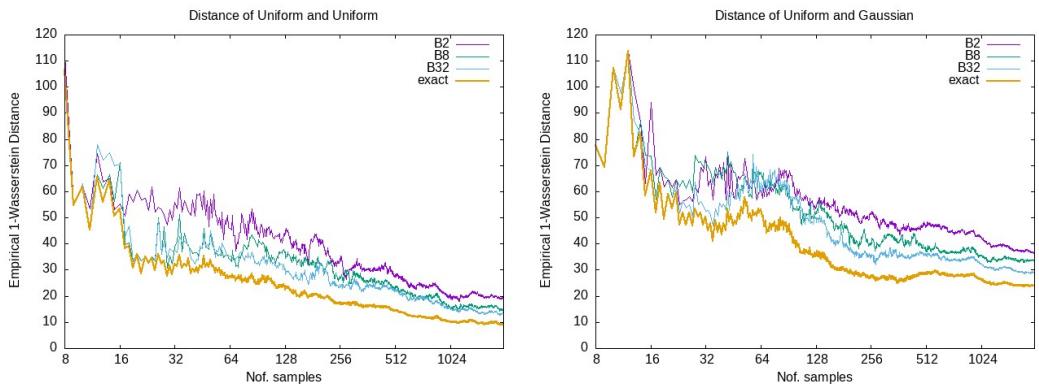
在这里，橙色线是精确解。其他线是具有不同网格参数 (\(p\)) 的近似值。虽然存在差距，但近似值完美地跟随了精确趋势。在许多机器学习应用中 (如训练 GAN) ，距离的梯度或趋势比精确的数值更重要，这使得这些近似非常有效。

结论

这篇关于“次线性更新时间的完全动态欧几里得双色匹配”的论文代表了算法上的重大进步。通过将线性时间更新转变为次线性时间 \(O(n^\varepsilon)\)，它为以前不可能实现的实时应用打开了大门。

其核心创新——嵌套网格、自底向上的贪心匹配以及通过运输问题实现的隐式表示——使得算法在更新期间可以忽略绝大多数数据集，仅关注受变化影响的特定空间区域。

对于几何优化领域的学生和从业者来说，这篇论文是一个完美的例子，展示了如果能够界定误差范围，放宽对“精确”解的要求是如何带来巨大的性能提升的。随着数据集持续增长到数百万甚至数十亿，这些次线性动态算法很可能成为处理运动中几何数据的标准。