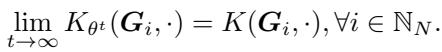引言

在机器学习的世界里，数据通常是整洁且呈表格形式的。但在现实世界中——尤其是在生物学、化学和社会科学领域——数据是杂乱且相互关联的。它们以图 (Graph) 的形式存在: 分子是由键连接的原子；社交网络是由友谊连接的人群。

为了理解这些数据，我们使用图卷积网络 (GCNs) 。 这些强大的神经网络可以预测诸如分子是否溶于水，或用户属于哪个社会群体等属性。我们将这项任务称为图属性学习 (Graph Property Learning) 。

但有一个问题。众所周知，GCN 的训练成本非常高昂。随着图数据集增长到数百万规模 (想想电子商务网络或庞大的化学数据库) ，训练这些模型的计算成本会急剧飙升。我们需要一种方法让它们学得更快，同时不牺牲准确性。

这就引出了一篇引人入胜的新研究论文: “Nonparametric Teaching for Graph Property Learners” (图属性学习者的非参数教学) 。

研究人员提出了一种名为 GraNT (Graph Neural Teaching，图神经教学) 的新范式。他们不再随机地向 GCN 投喂数据，而是引入了一位“教师”来策略性地选择最具信息量的样本。通过弥合图深度学习与非参数教学 (Nonparametric Teaching) 理论框架之间的差距，他们实现了超过 30-40% 的训练时间缩减。

在这篇文章中，我们将带你了解这个问题、解决方案背后的核心理论以及令人印象深刻的实验结果。

问题: 隐式映射的代价

从本质上讲，推断图的属性涉及学习一种映射。你将一个图 \(G\) 输入到一个函数中，它会输出一个属性 \(y\)。

在传统数学中，我们可能有一个公式。在深度学习中，这种映射是隐式 (implicit) 的。我们不知道具体的公式；我们正试图使用神经网络 (GCN) 来逼近它。

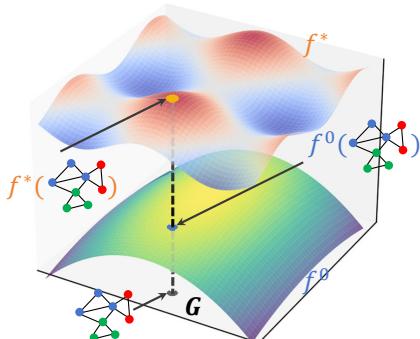
图 1: 图 G 与其属性 f*(G) 之间的隐式映射 f* 的示意图，其中 f0 表示初始图属性学习器 (例如，初始化的 GCN) 的映射。

如图 1 所示，假设分子结构与其能量状态之间的真实关系是曲面 \(f^*\)。我们的 GCN 从一个粗略的近似 \(f^0\) 开始。训练的目标就是扭曲 \(f^0\) 直到它与 \(f^*\) 匹配。

实现这一点的标准方法是随机梯度下降 (SGD): 选取一批图，检查误差，更新权重，然后重复。但在训练的所有阶段，并非所有图都同样有用。有些图很“简单”，教不了模型太多东西；有些图很“难”，能驱动显著的更新。随机采样忽略了这一点，导致了计算周期的浪费。

机器教学 (Machine Teaching) 领域致力于解决这个问题。它提出的问题是: 是否存在一组最佳的样本 (教学集) ，能比随机选择更快地引导学习器达到目标函数？

虽然机器教学已经存在了一段时间，但它通常假设目标函数是简单的 (参数化的) 。这篇论文将非参数教学——处理复杂的、函数空间的映射——应用到了图神经网络的世界。

理论桥梁

为了将教学理论应用于 GCN，作者必须解决一个脱节问题。

  1. GCN 使用梯度下降更新其参数 (权重) 。
  2. 非参数教学 在称为再生核希尔伯特空间 (RKHS) 的数学空间中更新函数本身。

为了让 GraNT 发挥作用，作者必须证明通过参数训练 GCN 在数学上与在函数空间中教导非参数学习器是一致的。

1. 结构感知更新

首先，让我们看看 GCN 是如何更新的。与独立处理输入特征的标准神经网络 (MLP) 不同，GCN 使用邻接矩阵 \(A\) 来聚合邻居的特征。

作者分析了一种“灵活 GCN (Flexible GCN)”。在这种架构中，特征在不同的“跳数 (hops)” (邻居、邻居的邻居等) 处被聚合并不联接。

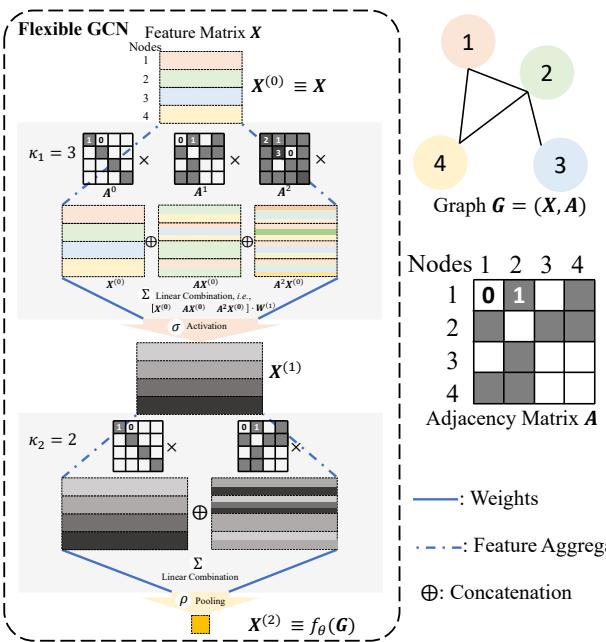
图 2: 以四节点图 G 为输入的两层灵活 GCN 的工作流程示意图。

图 2 展示了这个流程。输入特征 \(X\) 乘以邻接矩阵的幂 (\(A^0, A^1, A^2...\)) 以捕获结构信息。这些特征被组合，通过激活函数 (\(\sigma\))，并进行池化 (\(\rho\)) 以获得最终输出。

当我们计算梯度来更新权重时，邻接矩阵 \(A\) 已经融入到了数学运算中。作者推导了显式梯度，并发现参数更新是结构感知的 (structure-aware) 。 梯度的方向在很大程度上取决于图的拓扑结构，而不仅仅是节点特征。

2. 动态图神经切线核 (GNTK)

这是论文中最复杂也是最关键的部分。为了将参数更新连接到函数空间，作者利用了神经切线核 (Neural Tangent Kernel, NTK) 的概念。

简单来说，NTK 描述了神经网络在训练过程中是如何演变的。如果你将网络视为一个函数 \(f\)，那么该函数随时间的变化可以用一个核 \(K\) 来描述。

对于图来说，这就是图神经切线核 (Graph Neural Tangent Kernel, GNTK) 。

图 5: GNTK 计算的图形化说明。

图 5 可视化了这个核的计算过程。它本质上是从神经网络梯度的角度衡量两个图 (\(G\) 和 \(G'\)) 之间的相似性。它涉及计算输出相对于权重的梯度的点积。

作者证明了一个关键定理 (论文中的定理 5) :

源自 GCN 参数梯度下降的动态 GNTK，收敛于非参数教学中使用的结构感知规范核 (structure-aware canonical kernel)。

\[ \operatorname* { l i m } _ { t \infty } K _ { \theta ^ { t } } ( \pmb { G } _ { i } , \cdot ) = K ( \pmb { G } _ { i } , \cdot ) , \forall i \in \mathbb { N } _ { N } . \]

定理 5 极限方程。

这为什么重要? 这个证明是在 GCN 上使用非参数教学算法的“通行证”。它证实了通过标准反向传播演化 GCN 在数学上 (在极限情况下) 等同于在理想的教学空间中执行函数梯度下降。因为它们的行为方式相同，我们可以使用教学理论中的“贪婪选择”策略来加速 GCN 训练。

解决方案: GraNT 算法

建立了理论基础后，研究人员提出了 GraNT (Graph Neural Teaching)。

这个策略出奇地直观。如果 GCN 的更新等同于函数梯度更新，我们希望最大化该梯度以便尽可能快地收敛。

在数学上，最大化梯度更新大致等同于选择当前误差最大的数据点。

算法

“教师”不是在随机批次上训练，而是从数据集中选择特定的图来投喂给“学习者”(GCN)。

  1. 计算差异 (Discrepancy): 对于候选图池，计算 GCN 当前预测 \(f_{\theta}(G)\) 与真实属性 \(f^*(G)\) 之间的差异。
  2. 贪婪选择 (Greedy Selection): 选择差异最大的 \(m\) 个图。
  3. 更新 (Update): 在这 \(m\) 个“困难”的图上训练 GCN。
  4. 重复 (Repeat): 迭代执行此操作。

选择标准如下所示:

\[ \left\{ { { G } _ { i } } \right\} _ { m } ^ { * } = \underset { \left\{ { { G } _ { i } } \right\} _ { m } \subseteq \left\{ { { G } _ { i } } \right\} _ { N } } { \arg \operatorname* { m a x } } \left\| \left[ { { f } _ { \theta ^ { t } } } \left( { { G } _ { i } } \right) - f ^ { * } ( { { G } _ { i } } ) \right] _ { m } \right\| _ { 2 } . \]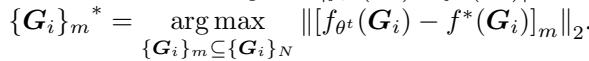

基于差异的选择方程。

GraNT 的两种形式

作者提出了两种变体来高效处理批处理:

  1. GraNT (B) - 批次级别: 教师查看现有的批次，并挑选平均误差最高的批次。这在计算上更便宜，因为不需要重新洗牌数据。
  2. GraNT (S) - 样本级别: 教师查看单个图，挑选最难的图，并将它们重新组织成新的批次。这更精确，但计算强度稍大。

课程学习 (Curriculum Learning): 请注意，一开始就不断给模型投喂最难的样本可能会让模型不堪重负。作者使用了一种课程策略: 在开始时，教师频繁地选择较小的子集 (以帮助模型“消化”) ，随着训练的进行，选择间隔逐渐变宽。

实验与结果

这个理论框架真的能带来更快的训练吗？作者在几个基准数据集上测试了 GraNT，包括 QM9 和 ZINC (分子属性回归) 以及 ogbg-molhiv (分类) 。

结果与标准训练循环 (“without GraNT”) 进行了对比。

图级任务 (分子)

这里的主要指标是墙上时间 (Wallclock Time) 对比 验证损失/误差 (Validation Loss/Error) 。 我们希望曲线尽可能快地下降到左下角。

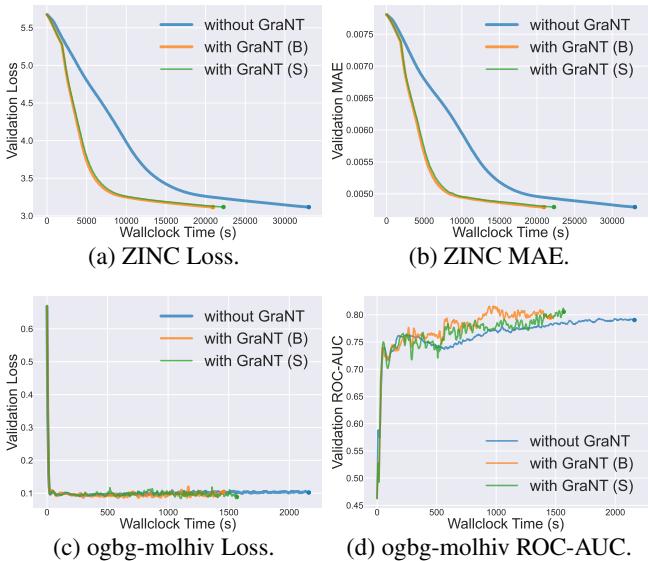
图 3: 图级任务的验证集性能: ZINC (回归) 和 ogbg-molhiv (分类) 。

图 3 讲述了一个令人信服的故事:

  • 图表 (a) 和 (b) 显示了 ZINC 数据集。蓝线 (Without GraNT) 表现得很“懒惰”；它需要很长时间才能降低误差。橙色 (GraNT B) 和绿色 (GraNT S) 线下降得明显更快。
  • 图表 (c) 和 (d) 显示了 ogbg-molhiv 分类任务。GraNT 比基准方法更早达到更高的 ROC-AUC 分数 (准确率) 。

就原始时间而言，节省是巨大的。

  • ZINC: 训练时间减少了 36.62% 。
  • ogbg-molhiv: 训练时间减少了 38.19% 。

节点级任务

该方法不仅限于对整个图进行分类。它也适用于对图中的特定节点进行分类。作者使用了合成数据集 (gen-reg 和 gen-cls) 来测试这一点。

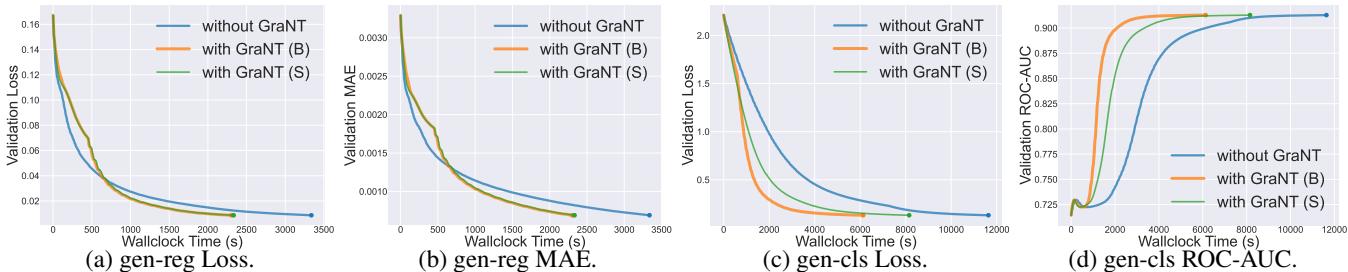
图 4: 节点级任务的验证集性能: gen-reg (回归) 和 gen-cls (分类) 。

图 4 显示了更具戏剧性的结果。看一看 图表 (c) (Loss) 和 图表 (d) (ROC-AUC)。GraNT 曲线 (橙色/绿色) 几乎立即飙升至高准确率，而标准训练 (蓝色) 则明显滞后。

  • 节点级分类: 训练时间减少了 47.30% 。

结果总结

下表总结了不同数据集的效率提升。关键的结论是，GraNT 始终能缩短训练时间 (通常缩短三分之一或更多) ，且不损害最终的测试性能 (误差/准确率指标相当或更好) 。

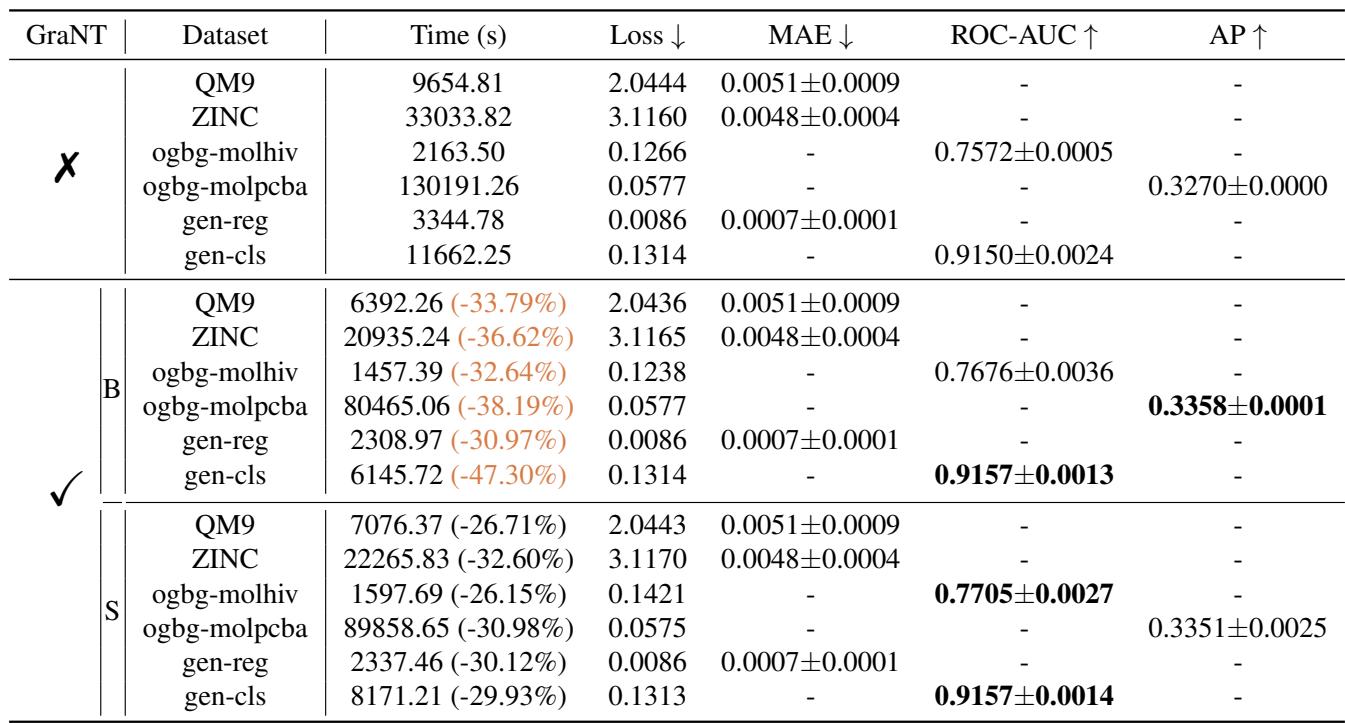
表 1: 不同基准测试的训练时间和测试结果。

GraNT (B) 和 GraNT (S) 两种变体的表现相似。GraNT (B) 通常更受欢迎，因为它更容易用标准的批次加载器实现，而 GraNT (S) 需要重新洗牌数据，这增加了一点开销。

结论与启示

论文 “Nonparametric Teaching for Graph Property Learners” 为一个实际问题提供了一个复杂的解决方案。通过非参数教学理论的视角审视图卷积网络，作者弥合了基于参数的学习与基于函数的教学之间的鸿沟。

主要收获:

  1. 理论一致性: 由于图神经切线核的特性，GCN 在训练期间的演变在数学上与非参数函数梯度下降一致。
  2. 贪婪即是好: 正是因为这种一致性，一个选择当前误差最大样本的贪婪“教师”，在加速收敛上是具有数学正当性的。
  3. 现实世界的速度: 这不仅仅是理论。GraNT 算法在标准基准测试中实现了 30-47% 的训练时间缩减。

这对未来意味着什么? 随着我们将 AI 应用于日益复杂的科学领域——如发现新抗生素或绘制蛋白质相互作用图谱——我们处理的图将变得巨大。像 GraNT 这样能让学习在数据和时间上更高效的技术，对于将这些模型从研究实验扩展为现实世界的工具至关重要。

GraNT 告诉我们，与其单纯地投入更多算力，不如更聪明地去教导我们的模型。