想象一下，你是一名探险家，被投放到一座迷宫般的巨大城市中——比如一个拥有数百万用户的社交网络，或者互联网的庞大拓扑结构。你肩负着一项使命: 你需要估算人口的平均收入，或者找到一个隐藏的机器人 (bot) 社区。你无法一次看清整张地图；你只能看到你所在的街道以及通往邻居的十字路口。

这就是经典的图采样 (Graph Sampling) 问题。为了解决这个问题，我们通常使用随机游走 (Random Walks) ——即在节点之间跳跃的虚拟代理。然而，简单的随机游走效率极低。它们容易陷入“死胡同” (紧密连接的社区) ，并浪费时间反复访问相同的节点。

近年来，研究人员开发了一种巧妙的修复方法，称为自排斥随机游走 (Self-Repellent Random Walk, SRRW) 。 它迫使探险家说: “我以前来过这里，我应该去别的地方。”虽然有效，但 SRRW 就像是背着沉重的背包徒步；决定下一步所需的数学计算非常繁重，以至于让探险家的速度慢得像蜗牛爬。

在这篇文章中，我们将深入探讨北卡罗来纳州立大学的研究人员在 ICML 2025 上提出的一个新框架: 历史驱动目标 (History-Driven Target, HDT) 。 这种方法保留了“自排斥”的智能，但卸下了沉重的背包。它不再为每一步计算复杂的物理过程，而是简单地改变了探险家使用的地图，从而使在大规模图上的高效采样成为可能。

问题所在: 陷入图的困境

图采样是网络科学的基础。无论是根据图数据训练 AI、爬取网页，还是分析区块链交易，我们都需要从目标分布 \(\mu\) (通常是所有节点的均匀分布) 中生成样本。

为此使用的标准工具是马尔可夫链蒙特卡洛 (MCMC) 。 一个“行走者”停留在一个节点上，选择一个邻居，并根据概率规则决定是移动还是停留。最著名的版本是 Metropolis-Hastings (MH) 算法。

虽然理论上是合理的，但标准的 MH 存在混合缓慢 (slow mixing) 的问题。如果图中存在“瓶颈”——即大型集群之间的狭窄桥梁——行走者往往会被困在一个集群中很长时间，然后才穿过桥梁。这导致我们的估计方差很高；仅仅因为我们还没有找到通往 B 集群的桥梁，我们可能会误以为整个世界看起来都像 A 集群。

以前的解决方案: SRRW

为了解决这个问题，研究人员引入了自排斥随机游走 (SRRW) 。 直觉很简单: 如果你访问了节点 A 十次，而节点 B 只有一次，那么接下来你应该更有可能移动到节点 B。

SRRW 通过修改转移核 (Transition Kernel) 来实现这一点——即从一个状态移动到另一个状态的实际概率机制。

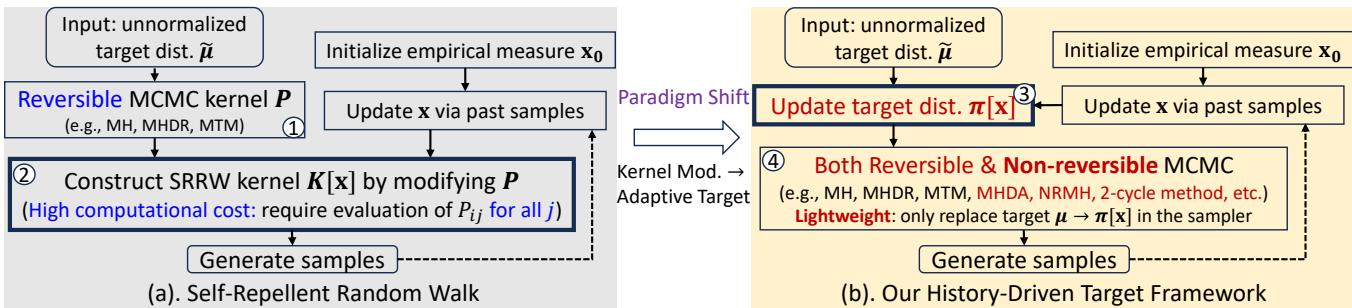
SRRW 和 HDT 之间的流程图比较。

如上图 Figure 1 (a) 所示，SRRW 过程涉及获取访问历史 (\(\mathbf{x}\)) ，并用它来构建一个新的核 \(K[\mathbf{x}]\)。这个核会主动将行走者推离频繁访问的状态。

SRRW 核的数学公式如下所示:

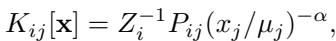
显示归一化常数 Z 的 SRRW 核方程。

在这里，\(x_j\) 是访问频率，\(\mu_j\) 是目标概率。项 \((x_j/\mu_j)^{-\alpha}\) 产生了排斥力。如果 \(x_j\) 很高 (经常访问) ，移动到那里的概率就会下降。

SRRW 的缺陷: 仔细看上面方程中的项 \(Z_i^{-1}\)。这是一个归一化常数 。 要计算它，你必须对移动到当前节点 \(i\) 的每一个邻居的概率进行求和。

如果你在一个有 5 个邻居的节点上，那没问题。如果你在一个“枢纽”节点上 (比如 Twitter/X 上的名人) ，拥有 100,000 个邻居，你就必须为了迈出一步而进行海量的计算。这种计算开销由抵消了效率增益。此外，SRRW 严格要求底层的马尔可夫链是“可逆的”，这排除了许多先进、更快的采样技术。

范式转变: 从核到目标

HDT 论文的作者提出了一个绝妙的问题: 既然我们可以直接改变目的地 (目标) ，为什么还要改变行走的物理规则 (核) 呢?

历史驱动目标 (HDT) 框架不再创建一个复杂的强制行走者远离过去状态的新转移规则，而是简单地向行走者“谎报”目标分布。

在标准 MCMC 中，行走者试图收敛到一个静态目标 \(\mu\)。在 HDT 中，我们将 \(\mu\) 替换为一个动态的、依赖于历史的目标 \(\pi[\mathbf{x}]\) 。

设计新目标

新目标分布 \(\pi[\mathbf{x}]\) 随时间演变。随着行走者积累历史 (由经验测度 \(\mathbf{x}\) 表示) ，目标会发生偏移，以优先考虑未被充分探索的区域。

这个新目标的公式既优雅又简单:

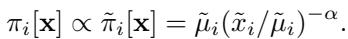
定义历史驱动目标分布的方程。

让我们分解一下:

  • \(\tilde{\pi}_i[\mathbf{x}]\) 是节点 \(i\) 的未归一化目标概率。
  • \(\tilde{\mu}_i\) 是原始目标 (例如，节点度数或均匀值) 。
  • \((\tilde{x}_i / \tilde{\mu}_i)^{-\alpha}\) 是反馈项。

如果节点 \(i\) 被访问的次数超过了它“应该”被访问的次数 (即 \(\tilde{x}_i\) 相对于 \(\tilde{\mu}_i\) 很大) ，该项就会变小。目标概率 \(\pi_i\) 随之降低。MCMC 采样器只是做着跟随目标的工作，自然会避开这个节点，因为它现在认为这个节点“不重要”。

相反，如果一个节点被访问不足，\(\pi_i\) 就会增加，像磁铁一样将行走者拉向未探索的区域。

为什么这是一场“轻量级”革命

这种方法的天才之处在于它如何与 Metropolis-Hastings (MH) 算法集成。在 MH 中，我们基于接受率 (Acceptance Ratio) 接受从节点 \(i\) 到节点 \(j\) 的移动。

因为 HDT 框架修改的是目标，而不是核机制，接受率变成了:

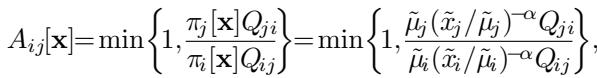
使用 HDT 目标的 Metropolis-Hastings 接受率。

注意到这里有什么关键点吗? 没有求和。 不存在需要检查所有邻居的归一化常数 \(Z_i\)。我们只需要当前节点 \(i\) 和提议节点 \(j\) 的值。

这将计算成本从 SRRW 中的 \(O(\text{neighbors})\) 降低到了 HDT 中的 \(O(1)\)。对于密集图或高维问题，这是巨大的速度提升。

算法: 如何运行

HDT 框架被设计成一个“即插即用”的模块。你可以采用任何现有的 MCMC 采样器 (基础 MCMC) 并用 HDT 进行升级。

算法的流程如下:

  1. 初始化 : 将行走者放置在一个节点上，并给每个节点一个微小的“虚假”访问计数 (以避免除以零) 。
  2. 循环 \(T\) 步:
  • 提议 : 使用你的基础采样器提议一个新状态 (例如，随机选择一个邻居) 。
  • 计算 : 使用上面的公式 (Image 009) 计算接受概率，该公式使用当前历史 \(\mathbf{x}\)。
  • 接受或拒绝 : 执行移动。
  • 更新历史 : 增加当前节点的访问计数。这会立即为下一步更新目标 \(\pi[\mathbf{x}]\)。

历史 \(\mathbf{x}\) 根据以下随机逼近进行更新:

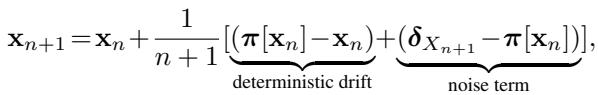
显示经验测度 x 更新规则的方程。

这个方程表明，历史 \(\mathbf{x}_{n+1}\) 是旧历史 \(\mathbf{x}_n\) 和新样本 \(\delta_{X_{n+1}}\) 的混合。这种持续的更新创建了一个反馈循环: 当你访问一个地方时，你会让它变得不那么有吸引力，迫使你继续前进。

理论保证: 它会收敛！

你可能会担心: “如果我们不断移动球门 (改变目标) ，行走者真的能描绘出真实的分布 \(\mu\) 吗？”

作者提供了严格的数学证明来回答“是的”。

1. 收敛性 (遍历性)

他们证明了经验测度 \(\mathbf{x}_n\) 几乎必然收敛到真实目标 \(\mu\)。该系统可以用微分方程 (ODE) 建模:

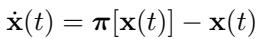
描述系统流动的微分方程。

系统自然地向 \(\pi[\mathbf{x}] = \mathbf{x}\) 的平衡点漂移。目标的设计确保了这种情况发生的唯一点是当 \(\mathbf{x} = \mu\) 时。

2. 方差缩减 (“零方差”效应)

标准随机游走的方差与图的“谱隙 (spectral gap) ”有关。如果间隙很小 (瓶颈) ，方差就会很大。

HDT 显著降低了这种渐近方差。方差按“排斥参数” \(\alpha\) 的比例缩小:

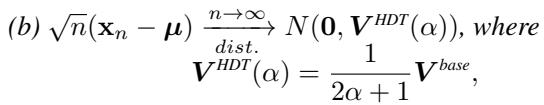
显示渐近方差减少 2 alpha + 1 倍的方程。

如果你设置 \(\alpha=0\)，你会得到标准方差 (\(V^{base}\))。随着你增加 \(\alpha\) (让行走者更强烈地厌恶重访) ，方差 \(V^{HDT}\) 会向零收缩。这意味着你需要更少的样本就能获得准确的估计。

3. 基于成本的优势

这是最关键的理论贡献。SRRW 也减少了方差，但它为此付出了昂贵的计算代价。

作者推导了一个基于成本的中心极限定理 。 他们比较了每单位计算预算 (\(B\)) 可实现的方差。

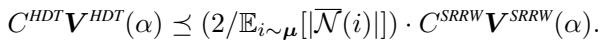
比较 HDT 与 SRRW 基于成本的方差的不等式。

这个不等式表明，HDT 的成本调整后方差比 SRRW 低一个大约等于平均邻居大小 (\(\mathbb{E}[|\mathcal{N}(i)|]\)) 的因子。

通俗地说: 在一个平均每个人有 500 个朋友的社交网络上，HDT 的效率大约是 SRRW 的 250 倍。

实验结果

理论听起来很棒，但在真实数据上效果如何？研究人员在几个真实世界的图上测试了 HDT，包括 Facebook 社交网络和点对点 (Gnutella) 网络。

准确性 vs. 步数

他们测量了总变差距离 (TVD) , 它量化了采样分布与真实分布之间的距离 (0 为完美) 。

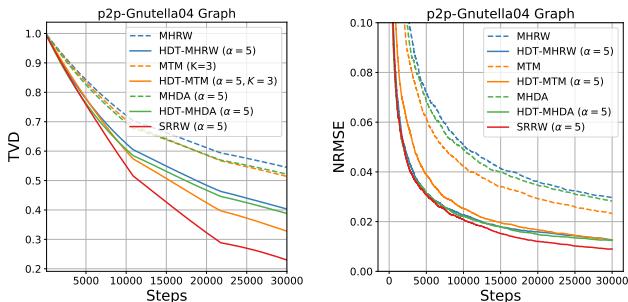
基础采样器与其 HDT 版本的 TVD 和 NRMSE 比较。

在 Figure 2 中，观察橙色虚线 (HDT-MHRW)。它比蓝色线 (标准 MHRW) 下降得快得多。这证实了添加历史驱动目标使采样器混合得更快。注意 SRRW (实心蓝线) 在步数方面也表现良好，但请记住——其中的每一步在计算上都很昂贵。

预算对决

当我们比较准确性与计算成本 (时间) 时，差异变得非常明显。

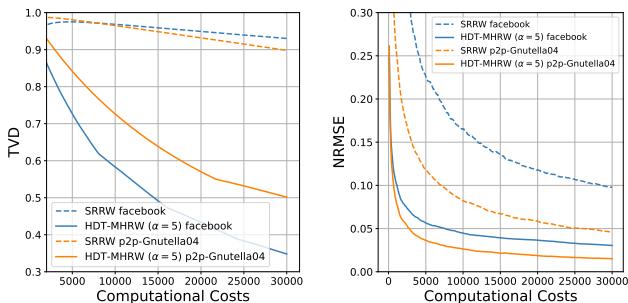
TVD 和 NRMSE 与计算成本的比较。

在 Figure 3 中，观察 Facebook 图的曲线。

  • SRRW (蓝色虚线) : 下降缓慢，因为它花费太多时间计算邻居概率。
  • HDT (橙色点线) : 像石头一样直线下坠。

因为 Facebook 图很密集 (平均度数高) ，SRRW受到了严厉的惩罚。HDT 几乎立即实现了低错误率。

灵活性: 不可逆链

以前的 SRRW 方法的主要限制之一是它只适用于“可逆”马尔可夫链 (如标准 Metropolis-Hastings) 。然而，现代 MCMC 使用“不可逆”链 (如 MHDA 或 2-cycle 游走) ，因为它们通过避免回溯，本质上混合得更快。

因为 HDT 修改的是目标而不是机制，它可以与不可逆链无缝协作。

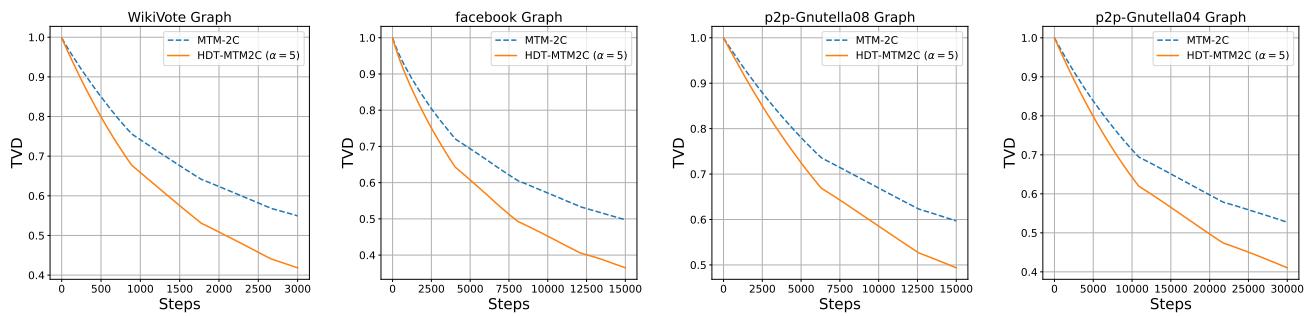
显示 HDT 改进 2-cycle 采样器的 TVD 比较。

Figure 7 展示了“2-cycle”采样器 (一种不可逆方法) 。实心橙色线 (HDT 版本) 始终优于标准版本 (虚线蓝色) 。这证明了 HDT 是图采样算法的通用助推器。

规模化: 内存挑战

有一个问题。要运行 HDT，你需要跟踪每个节点的历史 \(\mathbf{x}\) (访问计数) 。如果你的图有 1 亿个节点，存储一个大小为 1 亿的向量是非常消耗内存的。

作者提出了一个启发式解决方案: 最近最少使用 (LRU) 缓存 。

算法不再存储每个节点的历史，而是只记住最近访问过的节点。如果缓存满了，它会忘记最旧的访问。对于不在缓存中的节点，它会根据缓存中的邻居估计其访问频率。

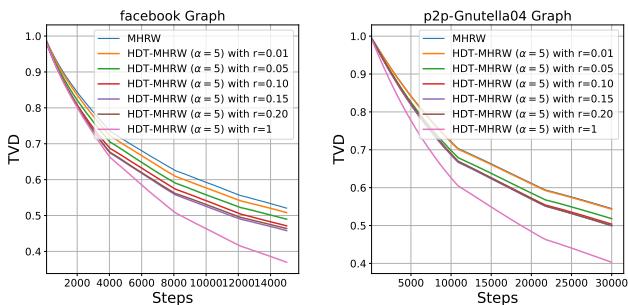
使用 LRU 缓存的 HDT 性能。

Figure 4 展示了 LRU 的性能。

  • 即使使用很小的缓存 (小 \(r\)) ，性能 (橙色/绿色线) 也明显优于标准随机游走 (从 TVD 1.0 开始) 。
  • 这表明局部的、最近的历史是自排斥的最重要因素。你不需要记住 10,000 步前做过什么来避免现在被卡住。

关键要点

历史驱动目标 (HDT) 框架代表了图上 MCMC 采样的重大进步。通过将“自排斥”机制从转移核转移到目标分布，作者实现了采样的“圣杯”:

  1. 高效率 : 接近零的方差，类似于以前的最先进方法。
  2. 低成本 : 更新是 \(O(1)\) 而不是 \(O(\text{neighbors})\)。
  3. 通用性 : 适用于几乎任何采样器 (可逆或不可逆) 。

对于数据科学的学生和从业者来说，这凸显了一个重要的教训: 有时解决复杂寻路问题的最佳方法不是构建一个更聪明的行走者，而是简单地画一张更好的地图。

参考文献

  • Doshi et al., 2023. Self-repellent random walks on general graphs.
  • Hu, Ma, & Eun, 2025. Beyond Self-Repellent Kernels: History-Driven Target Towards Efficient Nonlinear MCMC on General Graphs.