想象一下，你试图在黑暗中穿过一个拥挤的房间。你看不清楚；也许你手里只有一个光线微弱且闪烁不定的手电筒。你大致知道你的双腿是如何运作的 (你的动力学) ，但你对家具位置的感知 (环境) 是嘈杂且不确定的。如果你假设自己确切知道所有东西的位置，你很可能会踢到脚趾。如果你因恐惧而过度瘫痪，你可能根本无法移动。

这个场景概括了现代机器人技术中的一个基本挑战: 在测量不完美的情况下，在环境约束下学习未知的动力学。

在最近的一篇论文中，研究人员 Dongzhe Zheng 和 Wenjie Mei 提出了一个精妙的解决方案，弥合了微分几何和机器学习之间的鸿沟。他们的工作——Learning Dynamics under Environmental Constraints via Measurement-Induced Bundle Structures (基于测量诱导丛结构的约束环境下动力学学习) ——引入了一个数学框架，不仅将传感器噪声视为需要过滤掉的麻烦，反而将不确定性视为一种几何结构——具体来说，就是纤维丛 (Fiber Bundle) 。

在这篇文章中，我们将解构这篇论文，探索如何将测量、动力学和约束统一到一个单一的几何框架中，使机器人即使在传感器“撒谎”时也能安全地学习。

核心问题: 数学与现实的脱节

要理解这篇论文的重要性，我们需要先看看安全关键控制通常是如何处理的。

确保机器人不发生碰撞的黄金标准是控制障碍函数 (Control Barrier Function, CBF) 。 CBF 就像一个虚拟力场。当机器人接近不安全区域 (如墙壁) 时，CBF 的值会增大，迫使控制器转向避开。然而，经典的 CBF 通常假设机器人完全知道其状态 \(x\)。

在现实中，机器人依赖传感器。无人机使用激光雷达或摄像头；机械臂使用扭矩传感器。这些测量值 (记为 \(y\)) 通过测量映射 \(h(x)\) 加上一些噪声 \(v\) 与状态 \(x\) 相关联。

\[ \begin{array} { l } { { \dot { x } = f ( x , u ) + g ( x ) w , \quad x ( 0 ) = x _ { 0 } } } \\ { { \qquad y = h ( x ) + v } } \end{array} \]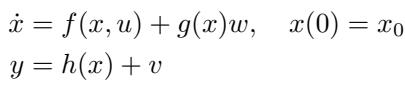

系统动力学和测量方程。

如上式所示，系统根据受干扰 \(w\) 影响的动力学 \(f(x, u)\) 演变，但我们只能观测到 \(y\)。

传统方法通常试图“清洗” \(y\) 以估计 \(x\) (使用卡尔曼滤波等滤波器) ，然后对该估计值应用安全规则。作者认为，这种做法将“感知”问题与“控制”问题分离得太开了。通过分离它们，我们失去了测量不确定性与约束之间的几何关系。我们需要一个框架，在这个框架中，不确定性本身决定了安全操作的几何形状。

几何解决方案: 纤维丛

作者的核心洞察是，测量不确定性不仅仅是概率噪声；它诱导了一种称为纤维丛 (Fiber Bundle) 的几何结构。

什么是纤维丛？

对于没有拓扑学背景的人来说，纤维丛听起来很吓人，但其直觉是很容易理解的。想象一片麦田。地面是底空间 (Base Space) (流形 \(\mathcal{M}\)，代表机器人的真实状态) 。从地面的每一点长出来的麦秆就是纤维 (Fiber) 。

在这个框架中，“全空间 (Total Space) ” \(\mathcal{E}\) 是状态空间和测量空间的结合。对于每一个真实状态 \(x\)，都有一组传感器可能报告的测量值 \(y\)，这些值受噪声限制约束。这组可能的测量值构成了 \(x\) 之上的纤维。

作者用数学方式定义纤维如下:

\[ { { \pi } ^ { - 1 } } ( x ) = \left\{ ( x , y ) \in { \mathcal { E } } : y = h ( x ) + v , \| v \| \leq \delta _ { v } \right\} \]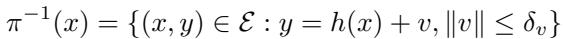

纤维丛逆投影的定义。

这里，\(\pi^{-1}(x)\) 表示状态 \(x\) 处的纤维。它包含所有状态和测量对 \((x, y)\)，其中测量值在真实测量映射的有界噪声距离 \(\delta_v\) 之内。

这为什么重要？通过将系统视为在“全空间” (状态加测量) 中移动，而不仅仅是在状态空间中，控制器可以自然地考虑到一个真实状态在传感器看来可能是许多不同的样子。

联络 (Connection) : 连接动力学与测量

在几何学中，如果你想从一个纤维移动到另一个纤维 (即，随着机器人移动，可能的测量集合如何变化？) ，你需要一个叫做联络 (Connection) 的数学对象。

联络 (用 \(\nabla\) 表示) 规定了当我们穿过状态空间时，几何结构如何“扭曲”。它将状态的动力学与测量的演变耦合在一起。

\[ \nabla _ { X } Y = \pi _ { * } ^ { - 1 } ( \nabla _ { \pi _ { * } X } ( \pi _ { * } Y ) ) + K ( x ) { \big ( } y - h ( x ) { \big ) } \]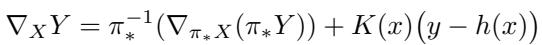

描述几何关系的联络方程。

在这个方程中，\(K(x)\) 是一个反馈增益算子。这是一种复杂的数学表达，意思是系统在全空间中的运动是机器人物理运动 (第一项) 和测量“误差”动力学 (第二项) 的结合。这种结构允许系统跟踪不确定性是如何随着机器人的移动而传播的。

不确定性的传播

当机器人执行轨迹时，过程噪声 (\(w\)) 和测量噪声 (\(v\)) 会相互作用。这种微分关系如下所示:

\[ \begin{array} { c } { { d \pi _ { * } ( X _ { f } ) = f ( x , u ) } } \\ { { d \pi _ { * } ( X _ { g } ) = g ( x ) w } } \\ { { d y = d h ( x ) + d v } } \end{array} \]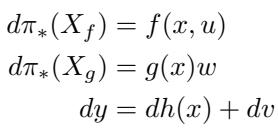

不确定性传播微分。

因为我们在丛上对此进行建模，不确定性不仅仅是一团概率云；它在名义轨迹周围形成了一个几何“管道 (tube) ”。

\[ \mathcal { T } _ { \varepsilon } ( x , t ) = \{ y : d y ( y , h ( \phi _ { t } ( x ) ) ) \leq \varepsilon ( t ) \} \]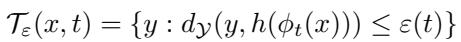

不确定性管道方程。

如果机器人能将其测量值保持在这个管道内，它就能保持概率性的安全保证。这种几何视角使得控制器能够具有“测量感知”能力。

测量感知控制障碍函数 (mCBFs)

标准的控制障碍函数说: “如果 \(h(x) \geq 0\)，你就是安全的。” 作者引入了测量自适应控制障碍函数 (Measurement-Adapted Control Barrier Functions, mCBFs) 。

mCBF 的核心思想是安全裕度应根据测量的质量进行调整。如果机器人处于传感器噪声大或纤维“很大”的状态，安全函数应该变得更加保守。

mCBF 的定义需要满足三个条件:

\[ \begin{array} { l } { 1 . \mathrm { ~ } b ( x , y ) \geq 0 \implies x \in \mathcal { S } _ { 0 } } \\ { 2 . ~ \underset { u \in \mathcal { U } } { \operatorname* { i n f } } \left[ L _ { f } b + ( L _ { g } b ) w + \alpha ( b ) \right] \geq 0 } \\ { 3 . \left| b ( x , y _ { 1 } ) - b ( x , y _ { 2 } ) \right| \leq L _ { b } d y ( y _ { 1 } , y _ { 2 } ) } \end{array} \]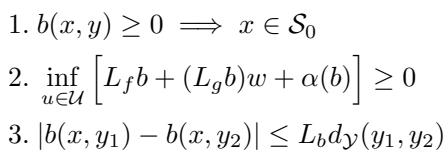

测量自适应控制障碍函数的条件。

让我们逐一分解:

  1. 安全蕴含 (Safety Implication) : 如果障碍函数 \(b(x, y)\) 为正，则真实状态 \(x\) 必须在安全集 \(\mathcal{S}_0\) 内。
  2. 前向不变性 (Forward Invariance) : 我们必须能够找到一个控制输入 \(u\)，使障碍函数保持为正 (保持安全) 。
  3. 利普希茨连续性 (Lipschitz Continuity，关键) : 如果测量值略有变化，安全函数的值不应剧烈跳变。这个条件限制了测量噪声能在多大程度上影响我们的安全感知。

自适应机制

mCBF 实际上是如何自适应的？作者提出了障碍函数的一种特定形式:

\[ \begin{array} { c } { { \Phi ( x , y ) = \Phi _ { 0 } ( x , y ) - \alpha ( \| y - h ( x ) \| ) } } \\ { { { } } } \\ { { L _ { f } \Phi + ( L _ { g } \Phi ) w \geq - \beta ( \Phi ) \mathrm { a l o n g ~ s o l u t i o n s } } } \end{array} \]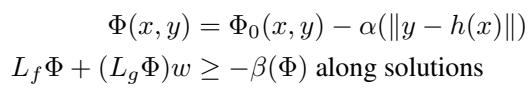

测量自适应安全证书公式。

注意这一项 \(-\alpha(\|y - h(x)\|)\)。随着测量值 \(y\) 与预期测量值 \(h(x)\) 之间的偏差增大，它会从安全裕度中扣除。

  • 良好的传感: \(y \approx h(x)\)，惩罚很小，机器人可以表现得更激进。
  • 糟糕的传感: \(y\) 偏离 \(h(x)\)，惩罚很大，安全边界有效地收紧。

概率性安全保证

由于噪声是随机的，保证通常也是概率性的。该框架证明，有了这些 mCBF，保持安全的概率非常高，并且以噪声水平为指数级边界。

\[ \mathbb { P } ( x ( t ) \in S _ { 0 } f o r a l l t \geq 0 ) \geq 1 - \exp ( - c / \delta _ { v } ^ { 2 } ) \]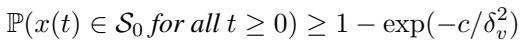

概率性安全保证定理。

该定理指出，保持在安全集 \(S_0\) 中的概率取决于测量噪声界限 \(\delta_v\)。随着传感器变得更好 (\(\delta_v\) 变小) ，安全性趋近于确定。

利用神经常微分方程学习动力学

到目前为止，我们讨论了几何和安全。但这篇论文也是关于学习的。机器人最初并不知道它自己的动力学函数 \(f(x, u)\)。

作者使用神经常微分方程 (Neural ODEs) 来近似动力学。然而，他们并不是简单地把神经网络扔给原始数据。他们使用丛结构来约束学习过程。

他们定义了一个在丛上作用的学习算子 \(\mathcal{L}\):

\[ \mathcal { L } ( \Phi ) ( x , y ) = \nabla \varepsilon \Phi ( x , y ) + \lambda R ( x , y ) \]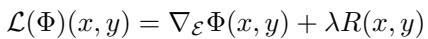

丛值学习算子。

学习到的动力学 \(\hat{f}\) 和障碍函数 \(\Phi\) 的更新法则由这些算子驱动:

\[ \begin{array} { l } { \dot { \hat { f } } = - \mathcal { L } _ { 1 } ( \hat { f } - f ) } \\ { \dot { \Phi } = - \mathcal { L } _ { 2 } ( \Phi - \Phi ^ { * } ) } \end{array} \]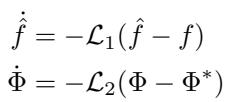

学习动力学方程。

通过将学习过程嵌入到几何框架中，神经网络被迫遵守系统的物理结构 (如旋转或平移中的对称性) 和测量约束。

实际的训练损失函数结合了动力学误差和不确定性加权范数:

\[ \begin{array} { c } { \displaystyle \dot { \theta } = - \Lambda \nabla _ { \theta } \mathcal { T } ( \hat { f } _ { \theta } , \mathcal { D } ) } \\ { \displaystyle \mathcal { T } ( \hat { f } , \mathcal { D } ) = \sum _ { i = 1 } ^ { N } \| \hat { f } ( x _ { i } , u _ { i } ) - \dot { x } _ { i } \| _ { \Sigma _ { i } ^ { - 1 } } ^ { 2 } } \end{array} \]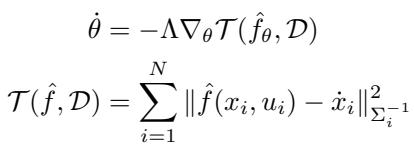

不确定性感知学习算法。

这里，\(\Sigma_i^{-1}\) 对误差进行加权。具有高不确定性 (嘈杂测量) 的数据点对梯度更新的贡献较小，从而防止神经网络“过拟合噪声”。

实验: 它有效吗？

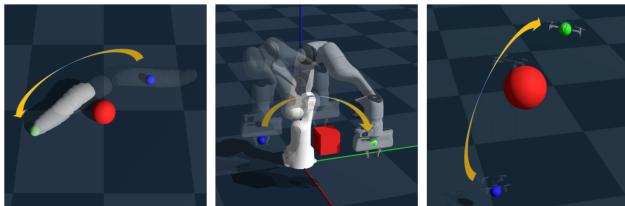
理论很优雅，但机器人学是一门实证科学。作者使用 Genesis 物理引擎在三个截然不同且具有挑战性的任务上验证了他们的框架。

实验设置

  1. 软体蠕虫机器人: 一个通过蠕动移动的软体机器人。它具有复杂的非线性动力学，并依靠视觉传感器避开障碍物。
  2. Franka Emika 机械臂: 一个执行操作任务的 7 自由度机械臂。它必须在抓取物体时避开障碍物，并处理关节摩擦和负载变化。
  3. 四旋翼无人机: 一个在 3D 空间中导航的飞行无人机，面临空气动力学扰动和深度测量噪声。

三个实验任务的插图: 蠕虫、Franka 机械臂和四旋翼无人机。

比较结果

作者将他们的方法 (“Ours”) 与几个最先进的基准方法进行了比较:

  • Neural-CBF: 使用神经网络作为障碍函数，但没有丛结构。
  • GPMPC: 高斯过程模型预测控制 (一种标准的概率方法) 。
  • SafetyNet & DataFilter: 其他安全学习方法。

如下面的收敛图所示，结果令人震惊。

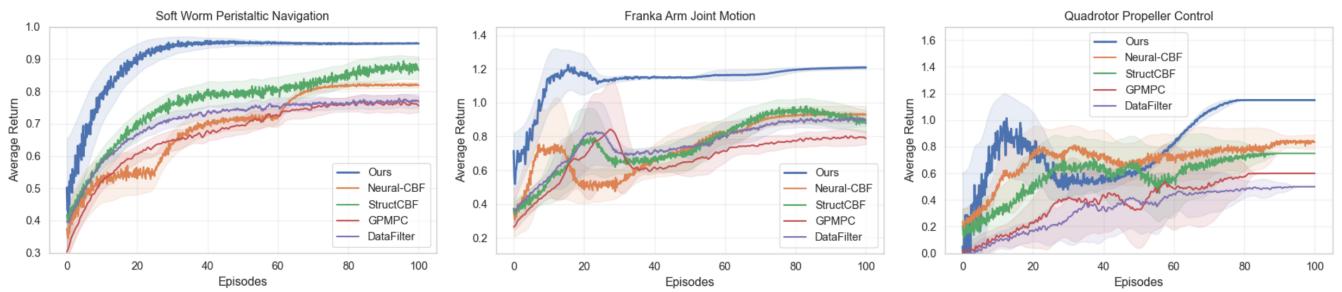
三个任务的训练收敛趋势。

在所有三个任务 (蠕虫、机械臂、无人机) 中，所提出的方法 (蓝线) 比基准方法更快地收敛到更高的回报 (更好的性能) 。阴影区域代表标准差——注意蓝色区域有多窄？这意味着该方法不仅更好，而且更一致、更稳定。

对噪声的鲁棒性

“测量诱导”框架的真正考验是当测量变差时会发生什么。作者在低、中、高三种噪声水平 (\(\sigma\)) 下测试了任务的成功率。

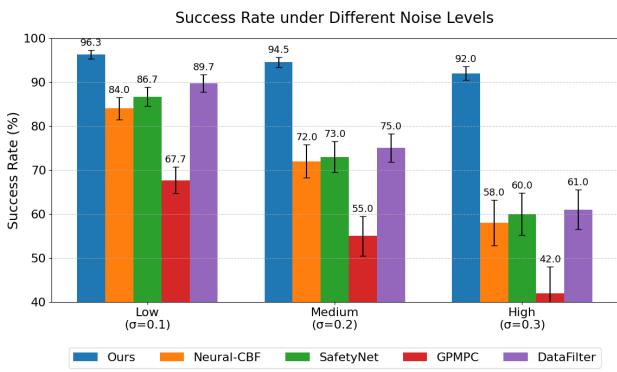
比较不同噪声水平下成功率的条形图。

如条形图所示:

  • 低噪声 (\(\sigma=0.1\)): 大家表现都不错，但“Ours”名列前茅 (96.3%)。
  • 高噪声 (\(\sigma=0.3\)): 这正是几何结构大放异彩的地方。像 Neural-CBF 这样的基准方法暴跌至 58% 的成功率。GPMPC 跌至 42%。而所提出的方法保持了 92.0% 的成功率 。

这证实了假设: 通过将测量不确定性嵌入到控制器的几何结构 (丛结构) 中，当传感器性能下降时，机器人自然会变得更加保守和鲁棒。

详细指标

数值结果凸显了轨迹的效率。

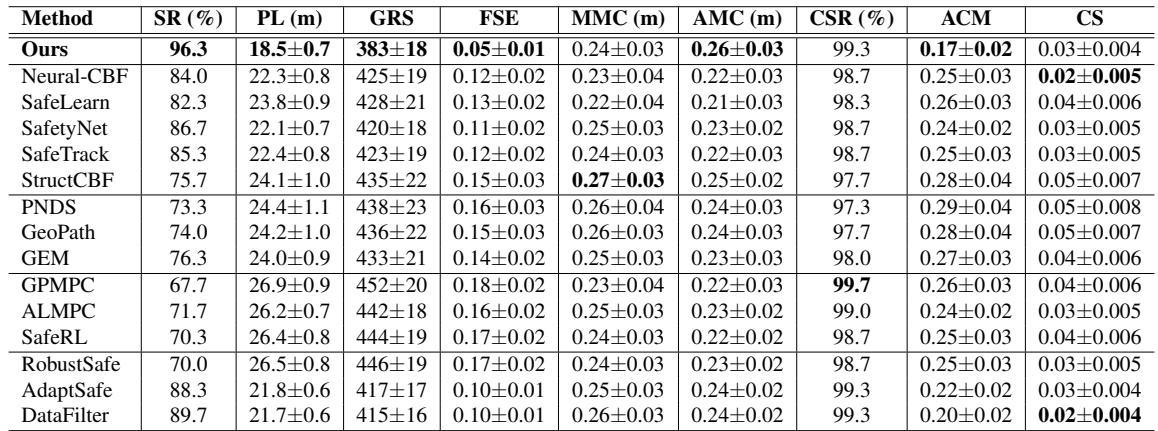
性能指标表。

查看表 1:

  • 成功率 (SR): 所提出的方法平均达到 96.3%，而 Neural-CBF 为 84%。
  • 路径长度 (PL): 路径更短 (18.5m 对比 22.3m) 。
  • 约束满足率 (CSR): 99.3%。

为什么路径更短而且更安全？传统的鲁棒方法 (如 RobustSafe) 通过过度保守来实现高安全性——它们在任何地方都假设最坏的情况，导致路径宽且效率低。丛框架是自适应的。它只在必要时 (高不确定性) 保守，而在测量清晰时保持高效。

丛结构真的重要吗？

作者进行了一项消融研究 , 看看复杂的几何结构是否真的起了关键作用。他们移除了 mCBF (安全性) 和丛结构，看看会发生什么。

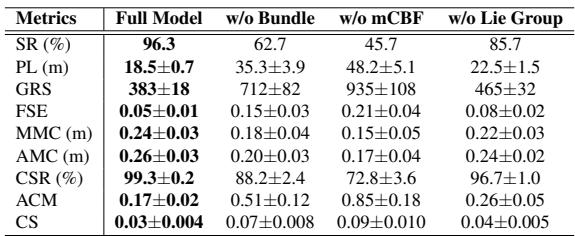
消融研究结果。

结果对非几何方法来说是毁灭性的:

  • 无丛结构 (w/o Bundle): 成功率从 96.3% 降至 62.7% 。 路径长度几乎翻倍。
  • 无 mCBF (w/o mCBF): 成功率降至 45.7% 。

这证明了将状态空间和测量空间视为统一的纤维丛不仅仅是数学上的门面装饰——它是性能提升的主要驱动力。

收敛性与理论

最后，作者为他们的实验成功提供了理论支持。他们证明了学习到的动力学 \(\hat{f}\) 以指数速度收敛于真实动力学 \(f\)，且残差受限于测量噪声 \(\delta_v\)。

\[ \begin{array} { r } { \| \hat { f } - f \| _ { \varepsilon } \leq c _ { 1 } \exp ( - \lambda _ { 1 } t ) + c _ { 2 } \delta _ { v } } \\ { \mathbb { P } ( x ( t ) \in { \mathcal S } _ { 0 } ) \geq 1 - \exp ( - c _ { 3 } / \delta _ { v } ^ { 2 } ) } \end{array} \]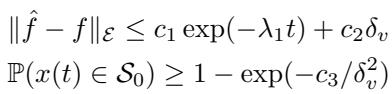

收敛性和安全保证不等式。

这让我们有信心，神经网络不仅仅是在死记硬背轨迹，而是实际上以足够高的精度近似了系统动力学，以维持安全性。

结论

这篇论文 Learning Dynamics under Environmental Constraints via Measurement-Induced Bundle Structures 提出了一个令人信服的论点: 几何很重要。

在追求自主系统的过程中，人们很容易完全依赖海量数据集和黑盒神经网络。然而，这项工作表明，通过尊重问题的底层几何结构——具体来说，就是机器人在哪儿与它看到什么之间的关系——我们可以取得明显更好的结果。

纤维丛框架实现了:

  1. 统一建模: 整合动力学、约束和传感器噪声。
  2. 自适应安全: 随环境不确定性而变化的安全裕度。
  3. 鲁棒学习: 有效学习且不过拟合传感器噪声的神经常微分方程。

对于机器人学和控制理论的学生来说，这代表着向“具身智能”的转变，即智能体的物理限制 (如传感器) 是其学习如何移动的核心，而不是被过滤掉的次要因素。