预测未来是人类最古老的愿望之一，也是数学上最困难的挑战之一。在数据科学领域，这转化为时间序列预测 。 虽然我们已经能够很好地预测下一个小时或明天的发生情况 (短期预测) ，但预测遥远的未来 (长期预测) 仍然是一个巨大的障碍。

当我们从点预测 (预测单个数值，如“25°C”) 转向概率时间序列预测 (PTSF) (预测一个分布，如“25°C，标准差为 2°C”) 时，难度会进一步增加。我们需要这些概率分布来在电网、金融市场和供应链中做出高风险决策。

今天，我们将深入探讨一篇新论文 K²VAE , 它提出了一种令人着迷的混合方法。该方法结合了Koopman 算子理论 (来自物理学) 、卡尔曼滤波 (来自控制理论) 和变分自编码器 (来自深度学习) ，以应对长期预测中固有的混沌特性。

问题所在: 混沌与误差累积

为什么长期概率时间序列预测 (LPTSF) 如此困难？

  1. 非线性: 现实世界的系统 (天气、交通、股价) 是非线性的。它们不是沿着直线发展，而是循环、突变，并表现出混沌行为。大多数统计模型难以在长周期内捕捉这些复杂的动态。
  2. 误差累积: 如果你的模型在第 1 步犯了一个微小的错误，这个错误会进入第 2 步，并呈指数级增长。到了第 720 步，预测结果通常就毫无用处了。
  3. 低效: 现代生成模型 (如扩散模型) 擅长处理分布，但计算量巨大。它们通常需要数百个迭代步骤才能生成一个预测，导致速度慢且占用大量内存。

研究人员在下图中生动地展示了这个问题。

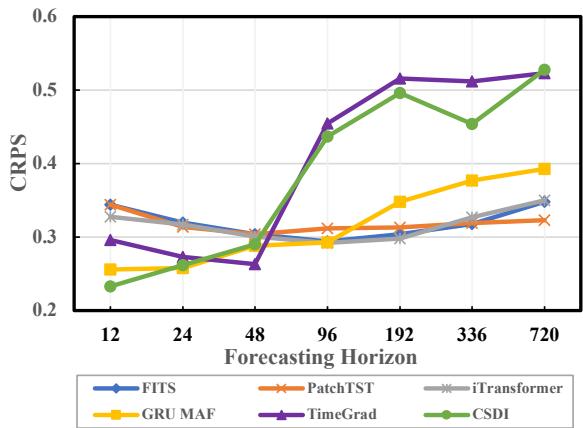
图 1: 预测模型对比。

如图 1 所示，随着预测范围的延长 (x 轴向右移动) ，标准概率模型的误差指标 (CRPS，越低越好) 会急剧恶化。事实上，点预测模型 (如 PatchTST) 的表现往往优于专门的概率模型，仅仅是因为概率模型在累积的不确定性重压下崩溃了。

核心理念: 非线性的线性化

K²VAE 的作者提出了一个巧妙的变通方法来解决非线性问题。如果不去尝试直接建模混沌的非线性曲线，而是将数据转换到一个不同的数学空间，在这个空间里行为变得线性 , 会怎么样？

这就是 Koopman 理论的前提。如果我们能找到合适的测量函数，我们就可以将非线性系统投影到一个更高维的空间，在那里它的演变受线性算子的控制。

然而，找到这个完美的线性表示是困难的。得到的线性系统通常是“有偏差的”或不完美的。这正是卡尔曼滤波发挥作用的地方。卡尔曼滤波是估计带有噪声或误差的线性系统状态的黄金标准。

K²VAE 代表 Koopman-Kalman 变分自编码器 (Koopman-Kalman Variational AutoEncoder) 。 其高级工作流程如下:

  1. KoopmanNet (Koopman 网络) : 将复杂的时间序列转换为简化的线性系统。
  2. KalmanNet (Kalman 网络) : 修正该线性系统并量化不确定性。
  3. VAE (变分自编码器) : 基于优化后的状态生成最终的概率预测。

让我们看一下高级数据流:

K2VAE 的数据流。

如图 2 所示，模型分解了任务。KoopmanNet 创建一个“有偏差的线性系统” (Biased Linear System，一个粗略的线性草图) 。然后 KalmanNet 接收这个草图，对其进行优化，并且——至关重要的是——计算“量化不确定性” (Quantitative Uncertainty，即置信区间) 。最后，解码器将所有内容映射回现实世界的数值。

理论基础

在剖析架构之前，我们需要简单了解一下名称中两个“K”的背景。

1. Koopman 理论

Koopman 理论指出，对于非线性动力系统 \(x_{k+1} = f(x_k)\)，存在一个无限维的测量函数空间 \(\psi\)，其中的转换是线性的。

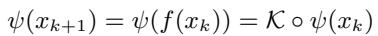
描述 Koopman 算子的方程。

在这里，\(\mathcal{K}\) 是 Koopman 算子。只要我们能学习到映射 \(\psi\)，它就允许我们使用简单的矩阵乘法向前推演时间，这在计算上既高效又稳定。

2. 卡尔曼滤波 (Kalman Filter)

卡尔曼滤波是一种用于估计线性系统状态的递归算法。它分两步进行:

  1. 预测 (Predict): 基于系统当前的物理状态估计下一个状态。
  2. 更新 (Update): 观察实际测量值，计算差异 (残差) ，并根据卡尔曼增益 (Kalman Gain) (我们在多大程度上信任模型 vs 测量值) 来调整预测。

在 K²VAE 中，卡尔曼滤波被实现为一个神经网络层 (KalmanNet)，以从数据中学习最佳增益和协方差矩阵。

K²VAE 架构

现在，让我们一步步拆解该模型。

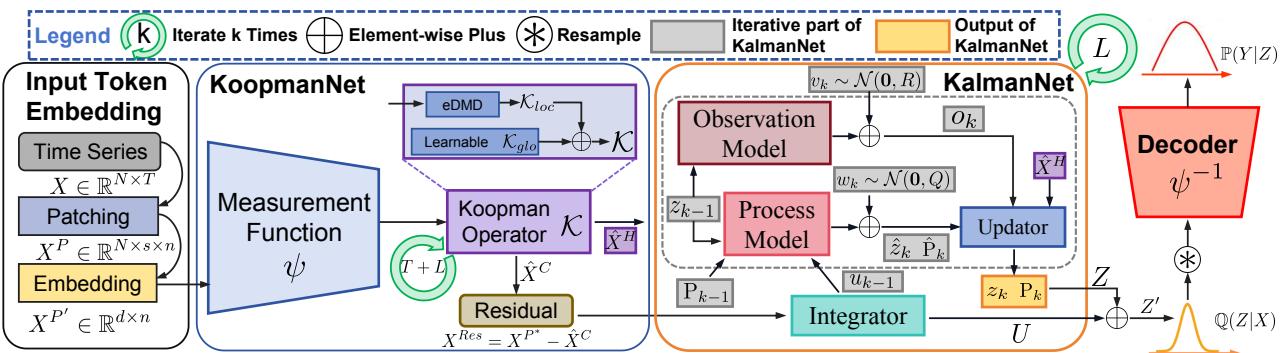
K²VAE 的架构。

步骤 1: 输入 Token 嵌入

时间序列数据通常是细粒度的。为了捕捉局部语义信息，模型首先使用一种称为分块 (patching) 的技术。它将时间序列分解为不重叠的片段 (patches) ，实际上是将时间序列片段像句子中的单词 (tokens) 一样处理。

分块方程。

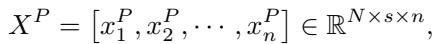
然后，这些片段被投影到高维嵌入空间。这使得模型能够隐式地捕捉多变量相关性 (不同变量之间的关系，如温度和电力使用量) 。

步骤 2: KoopmanNet (线性化)

编码器的第一个工作是线性化动力学。它使用神经网络 (MLP) 作为测量函数 \(\psi\)，将嵌入的 token 投影到“测量空间”。

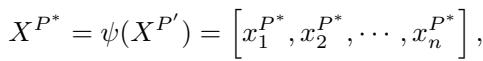
测量函数方程。

一旦进入这个空间，模型就会尝试拟合一个线性转移矩阵，即 Koopman 算子 \(\mathcal{K}\)。作者混合使用了纯数据驱动的方法 (使用一种称为扩展动态模式分解或 eDMD 的技术) 和一个可学习的全局算子。

通过迭代该算子，模型生成未来状态的预测。

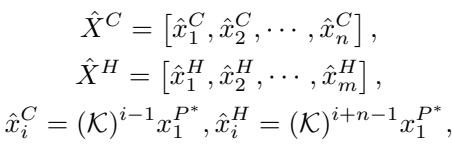
Koopman 预测方程。

这里，\(\hat{X}^C\) 是重建的上下文 (过去) ，\(\hat{X}^H\) 是预测的视野 (未来) 。因为学习到的测量函数永远不可能是完美的，所以这个线性系统是有偏差的 。 它捕捉了主要趋势，但遗漏了细微差别。

步骤 3: 利用积分器处理残差

为了修正偏差，模型会查看 Koopman 线性系统遗漏了什么。它计算残差 (实际投影与线性重建之间的差异) 。

一个基于 Transformer 架构的积分器 (Integrator) 处理这些非线性残差。

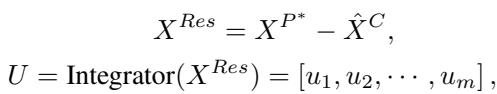
残差积分方程。

输出 \(U\) 代表了简单线性算子无法捕捉的非线性信息。这将作为卡尔曼滤波器的“控制输入”。

步骤 4: KalmanNet (优化与不确定性)

这是创新的核心。作者设计了一个 KalmanNet , 它将来自 KoopmanNet 的线性系统视为观测值，将非线性残差视为控制力。

KalmanNet 维护一个状态估计 \(z_k\)，以及至关重要的协方差矩阵 \(P_k\) 。 这个矩阵在数学上表示模型的不确定性——这正是我们进行概率预测所需要的。

预测步骤: 首先，KalmanNet 预测下一个状态和下一个不确定性协方差。

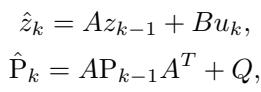
卡尔曼预测方程。

更新步骤: 然后，它利用来自 KoopmanNet 的信息修正这个预测。它计算卡尔曼增益 \(K_k\)，该增益决定了如何调整状态。

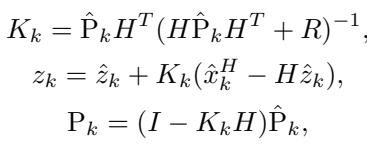
卡尔曼更新方程。

这一步有效地融合了线性趋势 (来自 Koopman) 和非线性调整 (来自积分器) ，同时通过 \(P_k\) 显式计算数据的分布。

步骤 5: 解码器 (生成输出)

最后，我们需要回到原始的时间序列数值。K²VAE 在这里使用了标准的变分自编码器结构。KalmanNet 给了我们一个优化后的状态 \(Z'\) 和不确定性 \(P\)。这些定义了一个变分分布 \(\mathbb{Q}(Z|X)\)。

模型从该分布中采样，并使用测量函数的逆 (\(\psi^{-1}\)) 将结果解码回时间序列域。

解码方程。

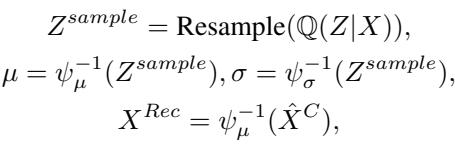
训练目标结合了 VAE 理论中的证据下界 (ELBO) 和重建损失，以确保线性系统与现实相符。

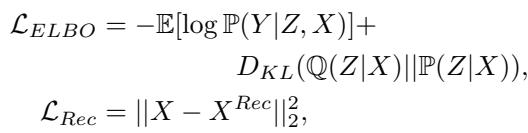
损失函数方程。

为何这种方法能胜出: 效率与准确性

K²VAE 架构相比基于扩散的模型 (如 TimeGrad 或 TSDiff) 具有明显的优势。扩散模型通过迭代地对随机噪声进行“去噪”来生成数据，通常需要通过网络进行数十次或数百次传递。

相比之下，K²VAE 依赖于矩阵乘法 (Koopman) 和递归更新 (Kalman) ，计算成本很低。

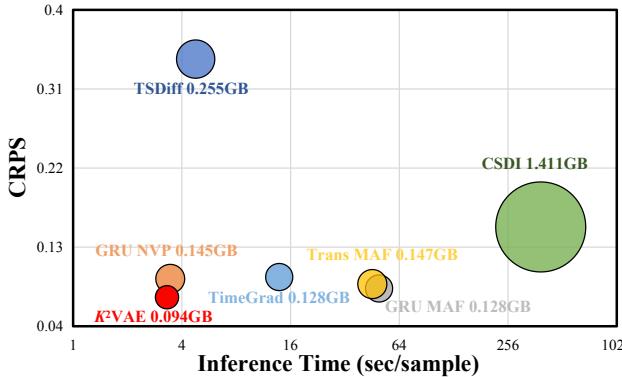
图 4: 效率对比。

图 4 绘制了连续分级概率评分 (CRPS，y 轴) 与推理时间 (x 轴) 的关系。理想情况下，你希望位于左下角 (快速且准确) 。

  • CSDI (绿色) : 非常准确 (在 y 轴上的位置较高实际上代表较差的 CRPS，因为越低越好。更正: 图注说明 CRPS 越低越好。CSDI 的 CRPS 约为 0.24，而 K2VAE 约为 0.05) 。CSDI 虽然准确，但速度极慢且占用大量内存。
  • K²VAE (红色) : 位于左下角。它实现了最低的误差 (CRPS ~0.05) ，同时速度比重型生成模型快约 10 倍到 50 倍。

实验结果

研究人员在广泛使用的基准数据集 (ETTh1, Electricity, Traffic, Weather) 上测试了 K²VAE，并与领域内的最佳模型进行了对比。

长期预测性能

长期预测 (预测未来 720 小时) 的结果尤为令人印象深刻。

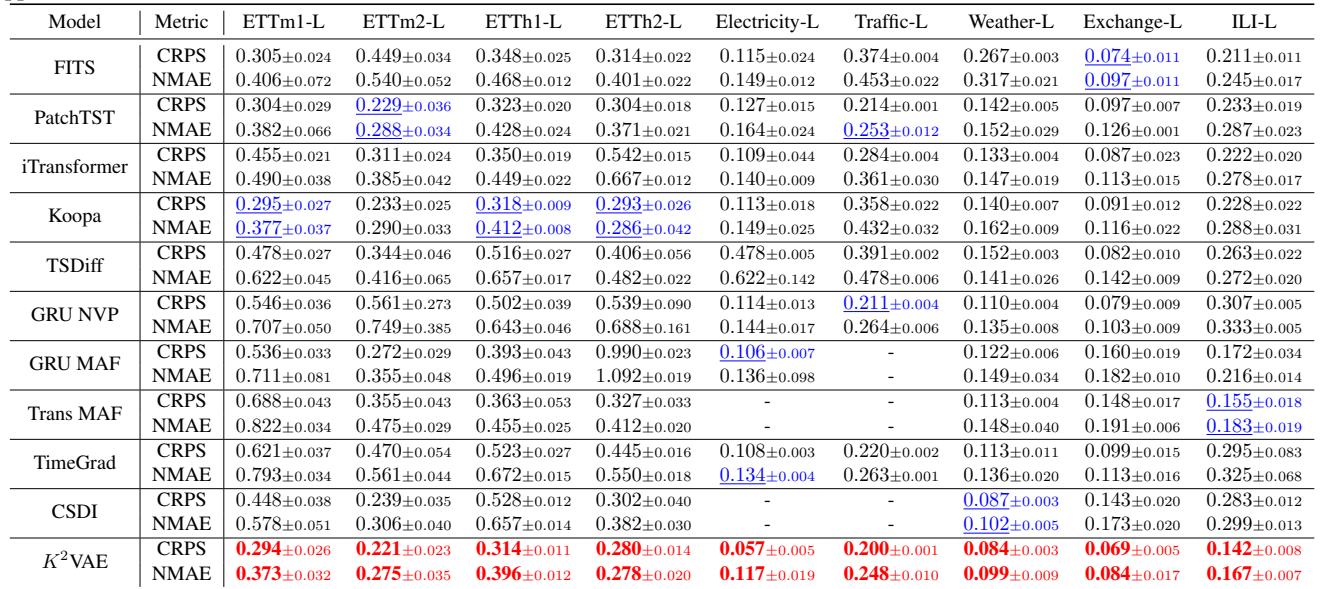
表 3: 长期预测结果。

在表 3 中，K²VAE (底行) 在几乎所有数据集上都始终取得了最佳 (粗体) 或第二佳 (下划线) 的结果。

  • 在 Electricity-L 数据集上，K²VAE 实现了 0.057 的 CRPS，误差几乎只有 Transformer 基线 (0.109) 的一半。
  • 它显著优于 TimeGrad 和 CSDI , 这两个是此前概率预测领域的最先进模型。

可视化不确定性

数字虽然很好，但在概率预测中，我们希望看到置信区间。模型知道它什么时候是不确定的吗？

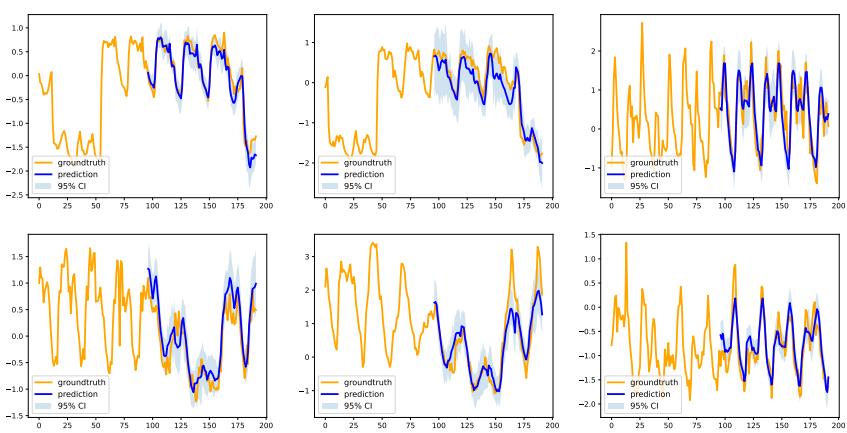
图 7: 电力数据集上的预测可视化。

图 7 展示了电力数据集上的预测。

  • 橙色: 真实值 (Ground Truth)。
  • 蓝色线条: 预测值。
  • 浅蓝阴影: 95% 置信区间。

请注意置信区间 (阴影区域) 是如何紧贴真实值的。即使序列出现尖峰或下降，真实值也很少落在模型的预测范围之外。这种可靠性对于电网管理等应用至关重要，因为低估方差可能导致停电或变压器过载。

短期性能

虽然该模型是为长期任务设计的，但它并没有牺牲短期准确性。

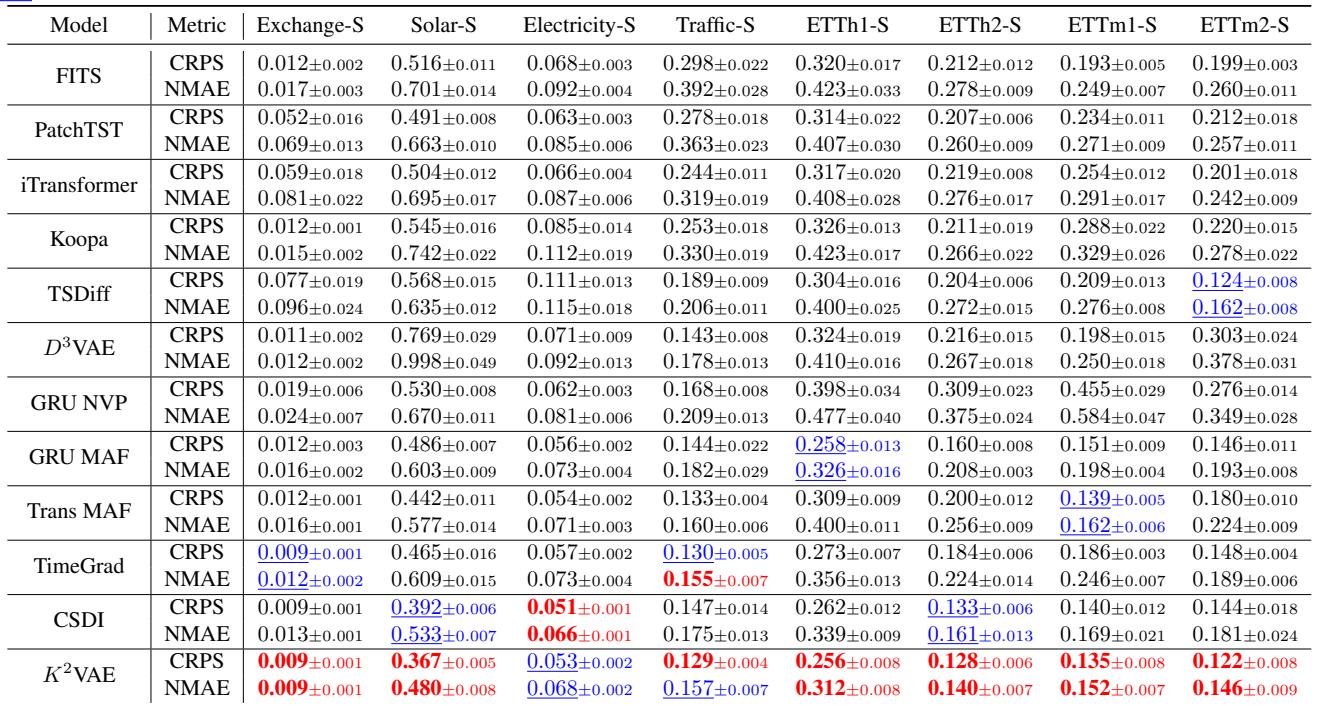
表 2: 短期预测结果。

如表 2 所示，K²VAE 在 Solar 和 Traffic 等数据集上仍然优于 PatchTST 和 TimeGrad 等专门的短期模型。这表明“线性化 + 优化”策略是一种稳健的通用时间序列动态建模方法，无论预测范围长短如何。

关键要点

K²VAE 论文提出了一个令人信服的论点，即从纯粹的“黑盒”深度学习转向融合物理原理的“灰盒”模型。

  1. 分而治之: K²VAE 没有强迫神经网络直接学习复杂的非线性混沌，而是拆分了问题。它利用 Koopman 理论找到线性简化，利用卡尔曼滤波处理混乱的现实。
  2. 显式不确定性: 通过在 VAE 中自然地使用卡尔曼滤波器的协方差矩阵，模型产生了严格的不确定性估计，而无需扩散模型集成那样沉重的计算成本。
  3. 速度至关重要: 在实时决策系统 (如高频交易或实时交通控制) 中，你不能等待几秒钟让扩散模型对预测进行去噪。K²VAE 的高效性使其具有高度的可部署性。

对于时间序列分析领域的学生和研究人员来说，K²VAE 证明了 20 世纪的经典理论——Koopman (1931) 和 Kalman (1960)——并未过时。当与现代深度学习相结合时，它们为我们最复杂的预测问题提供了最先进的解决方案。