开源 AI 的革命让强大的工具变得触手可及，从大型语言模型 (LLMs) 到文本生成图像生成器，不一而足。然而，这种便利性也带来了巨大的风险: 恶意微调。坏人可以获取一个安全的、公开的模型，并在包含有害内容的小型数据集上对其进行微调——无论是为了制作未经同意的深度伪造 (deepfakes) 、生成仇恨言论，还是设计恶意软件。

这就引出了一个紧迫的安全问题: 我们能否发布一个对不良行为“免疫”，但对预期用途仍然有用的模型?

这个概念被称为模型免疫 (Model Immunization) 。 直到最近，实现这一目标的方法主要还是经验主义的——即试错法，虽然看似有效，但缺乏坚实的理论基础。在这篇文章中，我们将深入探讨一篇名为*“Model Immunization from a Condition Number Perspective” (从条件数视角看模型免疫) *的研究论文。作者提出了一个基于海森矩阵 (Hessian matrix) 条件数 (condition number) 的数学框架，旨在“锁定”模型参数以防止有害更新。

如果你是一名熟悉梯度下降和基础线性代数的学生，你将看到这些基本概念是如何被用于 AI 安全防御的。

核心问题: 微调即优化

要理解免疫，我们首先需要看看坏人是如何修改模型的。通常，他们会执行迁移学习 (特别是线性探测或微调) 。他们采用一个预训练的特征提取器，冻结其大部分参数，然后使用有害数据集 \(\mathcal{D}_H\) 在其之上训练一个线性分类器。

从数学上讲，他们正在解决一个优化问题。他们想要找到权重 \(\mathbf{w}\) 来最小化损失函数 \(\mathcal{L}\):

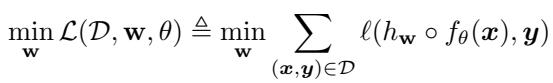
微调模型的优化目标。

这里，\(f_\theta\) 是预训练的特征提取器 (由 \(\theta\) 参数化) ，\(h_\mathbf{w}\) 是分类器。坏人使用梯度下降 (Gradient Descent) 来最小化这个损失。

学习速度与条件数

这就是论文的关键所在: 优化并不总是那么容易。 损失地形 (loss landscape) 的几何形状决定了梯度下降收敛到解的速度 (或者是否能收敛) 。

如果损失地形看起来像一个漂亮、圆润的碗，梯度下降会迅速到达底部。如果它看起来像一个又长又窄的山谷，优化器就会来回震荡，收敛得非常慢。

在线性代数中，这种几何形状由海森矩阵 (二阶导数矩阵) 的条件数 (\(\kappa\)) 来描述。矩阵 \(\mathbf{S}\) 的条件数定义为其最大奇异值与最小奇异值之比:

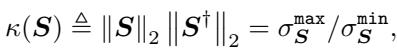
条件数 kappa 的定义。

为什么这很重要？因为最速下降法的收敛速度受限于这个数字。如果 \(\mathbf{w}^*\) 是最优解，\(\mathbf{w}_t\) 是第 \(t\) 步的权重，那么到解的距离按如下规律减小:

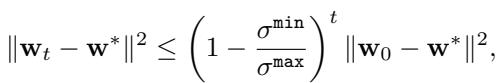
包含条件数的收敛速度不等式。

仔细看那个不等式。如果条件数 \(\kappa = \sigma^{\max} / \sigma^{\min}\) 非常大 (即一个“病态”问题) ，项 \((1 - \frac{\sigma^{\min}}{\sigma^{\max}})\) 就会变得非常接近 1。这意味着误差只能一点一点地极其缓慢地缩小。收敛将耗费极长的时间。

免疫的洞察: 如果我们能强迫有害任务的条件数变得巨大 (理想情况下是无穷大) ，坏人的梯度下降基本上就会停滞。他们将无法微调模型。

免疫框架

作者根据涉及条件数的三个具体要求定义了一个“免疫”模型。设 \(\theta^I\) 为我们免疫后的特征提取器参数。

1. 盾牌 (The Shield) : 与直接在原始数据上相比，使用免疫后的特征在有害任务 \(\mathcal{D}_H\) 上进行微调必须困难得多。

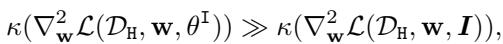
不等式显示有害任务的条件数应该非常大。

2. 效用 (The Utility) : 我们不能破坏模型在有用的、安全任务 (\(\mathcal{D}_P\)) 上被微调的能力。主要任务的条件数应保持在较低水平。

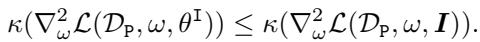
不等式显示主要任务的条件数应保持较低。

3. 性能 (The Performance) : 模型应仍能在原始预训练任务上表现良好。

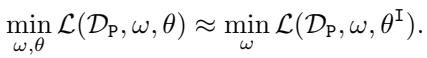
近似公式显示主要任务上的损失应保持相似。

线性情况

为了使理论在数学上易于处理，作者分析了线性模型 。 他们假设特征提取器是一个线性变换 \(\theta\)。如果坏人使用最小二乘 (\(\ell_2\)) 损失，优化问题看起来像这样:

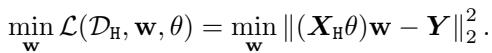
最小二乘目标函数。

在这个特定设置中，损失函数的海森矩阵 (决定了损失地形的曲率) 有一个封闭形式:

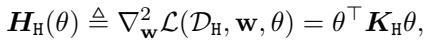
有害任务的海森矩阵定义。

这里，\(\mathbf{K}_H\) 是有害数据的协方差矩阵。作者推导出一个命题，表明这个海森矩阵的奇异值 (\(\sigma_i\)) 取决于特征提取器 \(\theta\) 的奇异向量与数据协方差之间的对齐程度。

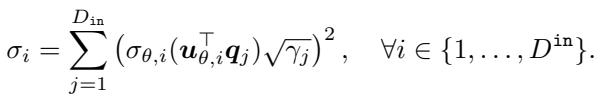
海森矩阵奇异值的方程。

这个方程证实了，通过操纵 \(\theta\)，我们可以控制奇异值——从而控制海森矩阵的条件数。

算法: 控制条件数

所以，我们有了一个计划: 在预训练期间修改 \(\theta\)，使得有害任务的海森矩阵是病态的 (高 \(\kappa\)) ，而有用任务的海森矩阵是良态的 (低 \(\kappa\)) 。

为了通过梯度下降实现这一点，我们需要可以将可微的正则化项添加到我们的损失函数中。作者提出了一个包含三个部分的目标函数:

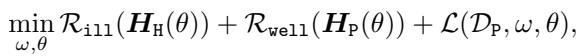
包含 ill 和 well 正则化项的总损失函数。

让我们来分解这两个正则化项，\(\mathcal{R}_{ill}\) 和 \(\mathcal{R}_{well}\)。

1. “良态”正则化项 (\(\mathcal{R}_{well}\))

这一项改编自先前的工作。它鼓励矩阵拥有小的条件数 (使优化变得容易) 。它本质上是试图让矩阵保持接近一个缩放的单位矩阵。

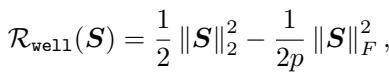
R_well 正则化项的定义。

当我们最小化这一项时，我们在压低条件数，确保模型对合法任务仍然有用。

2. “病态”正则化项 (\(\mathcal{R}_{ill}\))

这是论文的新颖贡献。我们需要一种方法来最大化条件数。然而，条件数本身很难直接优化，因为它是非凸且不连续的。

作者引入了 \(\mathcal{R}_{ill}\)，这是一个可微的代理，它是对数条件数倒数的上界。

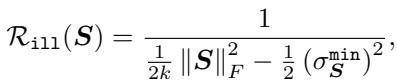
R_ill 正则化项的定义。

让我们解读这个分数。分母包含 \(\|\mathbf{S}\|_F^2\) (奇异值的平方和) 减去一个涉及最小奇异值的项。通过最小化整个项，我们实际上是在驱动分母趋向于零，这发生在条件数趋向于无穷大时。

作者证明了这个正则化项是可微的 (在温和的假设下) ，并提供了它的梯度:

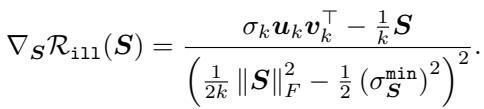
R_ill 正则化项的梯度。

至关重要的是，他们证明了采取梯度步骤来最小化 \(\mathcal{R}_{ill}\) 保证能单调地增加条件数。

更新规则

定义了这些正则化项后，免疫过程就变成了一个修改后的训练循环。我们在主要任务上训练模型，同时推动梯度以满足我们的条件数约束。

特征提取器 \(\theta\) 的更新规则如下所示:

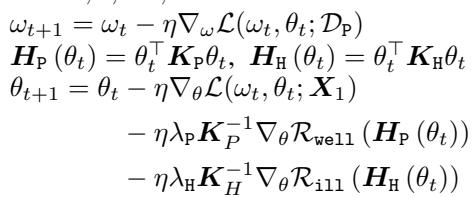
theta 的算法更新步骤。

注意更新 \(\theta_{t+1}\) 的三个组成部分:

  1. 来自任务损失的标准梯度 (\(\nabla_\theta \mathcal{L}\)) 。
  2. 在主要数据上最小化 \(\mathcal{R}_{well}\) 的项 (保持其有用) 。
  3. 在有害数据上最小化 \(\mathcal{R}_{ill}\) 的项 (使其具有抵抗力) 。

作者还推导了这些正则化项相对于特征提取器 \(\theta\) 的具体梯度:

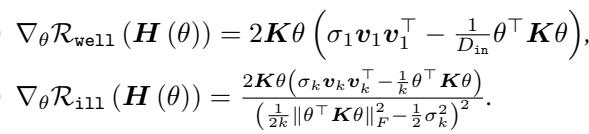
正则化项相对于 theta 的梯度。

实验与结果

这个数学理论在实践中站得住脚吗？研究人员在线性模型和深度神经网络上测试了该算法。

为了衡量成功，他们引入了相对免疫比率 (Relative Immunization Ratio, RIR) 。

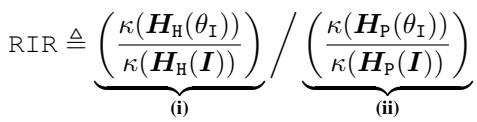
相对免疫比率 (RIR) 的定义。

  • 分子 (i): 我们让有害任务变得难了多少？ (我们希望这个值很高) 。
  • 分母 (ii): 我们让有用任务变得难了多少？ (我们希望这个值很低，理想情况下是 1) 。
  • 目标: RIR \(\gg 1\)。

线性模型: 房价预测和 MNIST

首先，他们在线性回归任务 (房价预测) 和分类任务 (MNIST) 上进行了测试。

房价预测: 下表比较了他们的方法 (“Ours”) 与基线方法如 “IMMA” (一种先前的双层优化方法) 和 “Opt \(\kappa\)” (直接优化条件数) 。

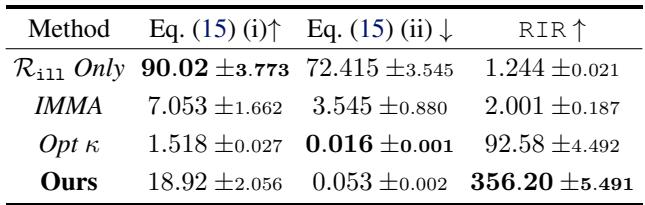
表 1: 房价数据集上的结果。

  • 看 RIR 列: 提出的方法实现了惊人的 356.20 的 RIR。
  • 看 (ii): 有用任务的条件数比率是 0.053，意味着有用任务实际上变得更容易优化了 (这是一个令人高兴的副作用) ，而有害任务变得难了 18 倍 (列 i) 。

收敛速度: 下图可视化了随时间变化的“学习曲线” (范数比率) 。

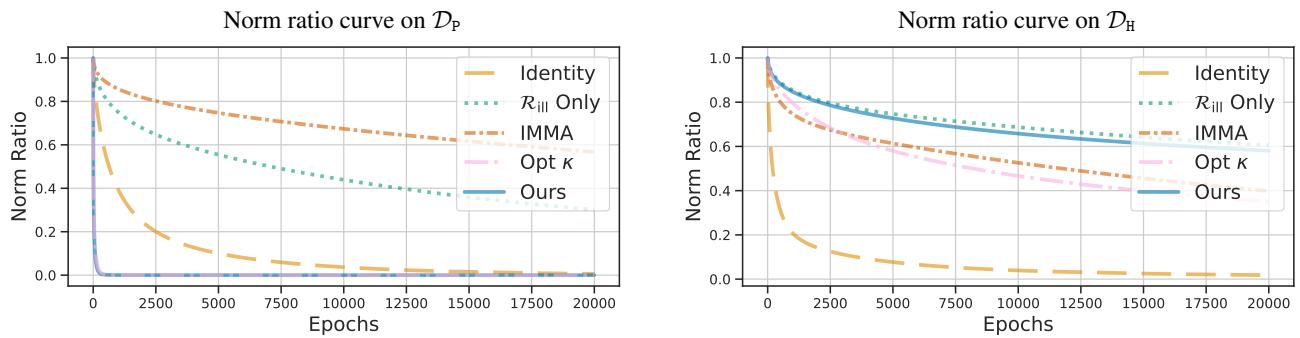
图 1: 收敛速度。

  • 左图 (主要任务) : 蓝线 (Ours) 下降最快。模型能迅速学习有用任务。
  • 右图 (有害任务) : 蓝线保持在高位。模型拒绝有效地学习有害任务。

MNIST 热图: 他们还在 MNIST 的所有数字对上运行了该算法 (例如，让“1 vs 7”成为有害任务，“3 vs 8”成为有用任务) 。

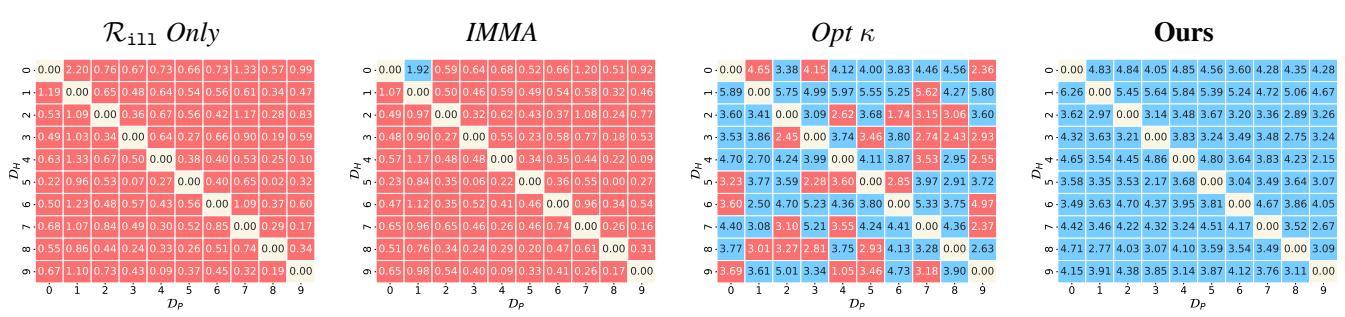
图 2: MNIST 上的 RIR 热图。

最右边的网格 (“Ours”) 几乎全是蓝色的，表明在几乎所有数字组合中免疫都成功了。基线 (左边的网格) 显示出大量的红色 (失败) 。

深度网络: ImageNet

最后，作者将此方法应用于在 ImageNet 上预训练的深度非线性模型 (ResNet18 和 ViT) 。他们将 ImageNet 视为“安全”任务，将 Stanford Cars 或 Country211 等数据集视为“有害”任务。

由于深度网络是非线性的，海森矩阵不完全是 \(\theta^\top K \theta\)，但我们可以通过查看特征表示的条件数来近似这种效果。

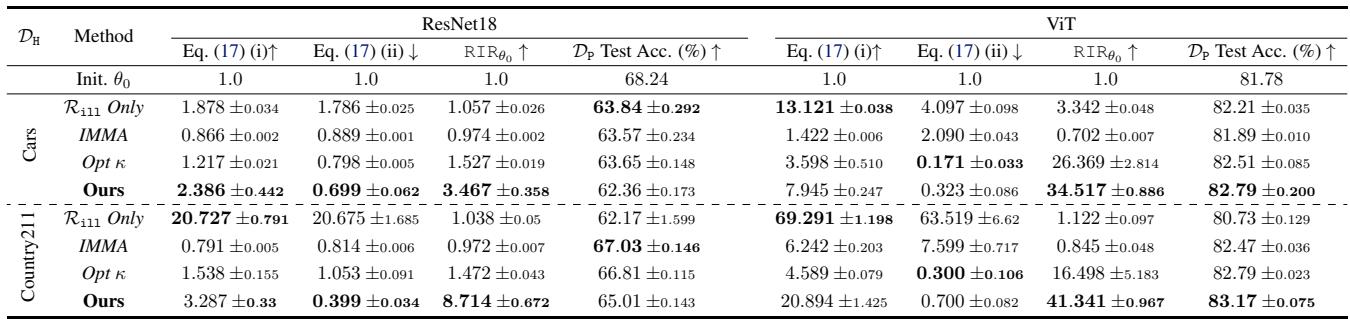
表 3: ImageNet 模型上的定量结果。

表 3 中的结果显示，“Ours” 始终能实现最高的 RIR。例如，在 Stanford Cars 上的 ViT 模型中，他们实现了 34.5 的 RIR，同时保持 (甚至略微提高) 了 ImageNet 上的测试准确率 (82.79%) 。

下图显示了微调期间有害任务的测试准确率。

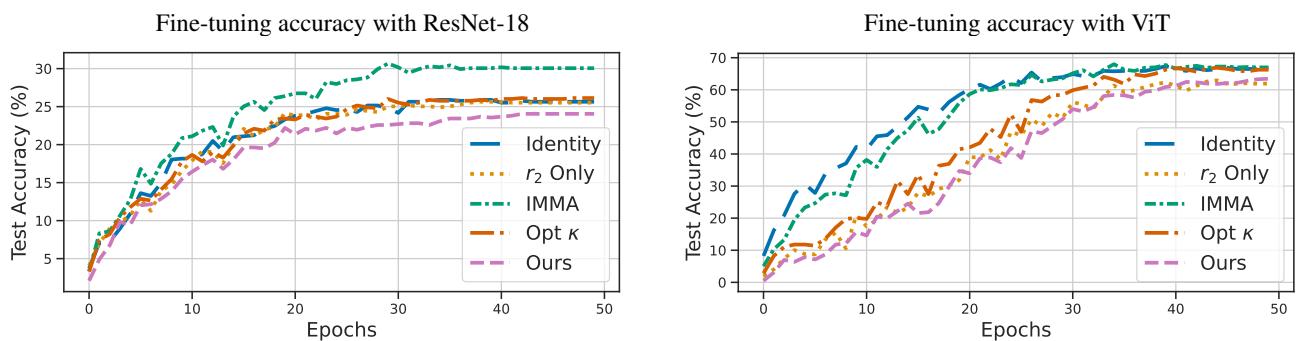
图 3: 深度网络在有害任务上的测试准确率。

  • 品红线 (Ours) : 注意它是如何落后于其他线条的。即使经过多次微调，使用该方法免疫的模型在有害任务上的准确率仍然最低。这种免疫创造了一种对学习不良概念的“抵抗力”。

结论与意义

这就弥合了模型安全经验实践与优化理论基础之间的差距。通过条件数的视角来看待模型免疫，作者提供了:

  1. 关于模型免疫含义的精确定义 。
  2. 一种新颖的正则化项 (\(\mathcal{R}_{ill}\)) ，可证明能最大化条件数。
  3. 一种有效保护线性及深度模型的算法 。

这种针对 AI 模型的“疫苗”预示着未来发布的开源模型可以带有一层数学保护，防止坏人轻易地将其重用于危害目的，同时保留开放获取带来的科学和商业利益。虽然没有一种防御是完美的，但将优化地形变成攻击者难以逾越的“险恶山谷”是一种强大的威慑。