超越温度参数: 利用软推理与贝叶斯优化引导大模型思维

如果你曾经尝试过让大语言模型 (LLM) 解决复杂的数学问题或棘手的逻辑谜题，你可能体会过模型产生“幻觉”或推理偷懒带来的挫败感。你问了一个问题，模型却自信地给出了错误的答案。

为了解决这个问题，我们通常依赖两种主要策略。第一种是提示工程 (Prompt Engineering) ——例如告诉模型“一步一步地思考” (思维链) 。第二种是解码策略 (Decoding Strategies) ——具体来说就是调整“温度 (temperature) ”。如果模型卡住了，我们就调高温度以增加随机性，希望在一批 10 个或 20 个生成的答案中，能有一个是正确的。

但是，增加随机性真的是探索解法的最佳方式吗？高温是一个生硬的手段；它会使概率分布变得平坦，让模型说出胡言乱语的概率和找到创造性解法的概率一样高。

一篇引人入胜的新论文《Soft Reasoning: Navigating Solution Spaces in Large Language Models through Controlled Embedding Exploration》 (软推理: 通过受控嵌入探索在大语言模型中导航解空间) 提出了一种更聪明的方法。研究人员没有随机地动摇模型 (调整温度) 或乞求它更加努力 (提示工程) ，而是引入了一种利用贝叶斯优化从数学上引导模型内部“思维过程”的方法。

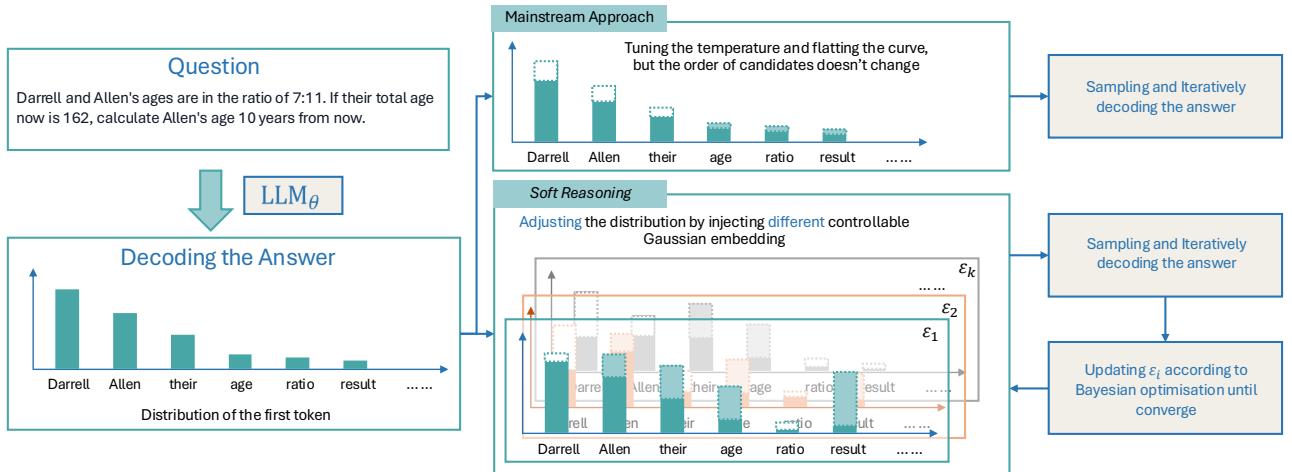
主流方法与本文提出方法的对比。

如图 1 所示，主流方法依赖于随机采样，而 Soft Reasoning (软推理) 则向模型的嵌入 (embeddings) 中注入精确、受控的噪声，并对该噪声进行优化以找到最佳答案。在这篇文章中，我们将拆解这一架构，以此理解如何在不触及模型权重的情况下控制 LLM 的推理。

当前解码方式的问题

要理解为什么 Soft Reasoning 是必要的，我们首先需要看看 LLM 是如何生成文本的。在每一步，模型都会预测词表中每个词的概率。

在贪婪解码 (Greedy Decoding) 中，模型总是选择概率最高的词。这很稳定，但也是重复的。它经常陷入“局部最优解”——如果数学问题的第一步稍微有点错，整个解法就会失败。

为了解决这个问题，我们通常使用温度缩放 (Temperature Scaling) 。 在时间步 \(t\) 选择 Token \(w^{(t)}\) 的概率由温度参数 \(\tau\) 调整:

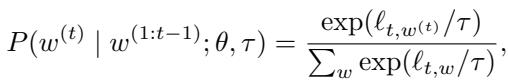
温度缩放概率分布的公式。

当 \(\tau\) 较高时，分布会变平。低概率的词变得更有可能被选中。这创造了多样性，但这是“盲目”的多样性。模型不知道哪些低概率词是巧妙的转折，哪些只是胡言乱语。

更先进的方法，如思维树 (Tree of Thoughts, ToT) 或蒙特卡洛树搜索 (MCTS) , 试图显式地探索不同的推理路径。然而，这些方法计算成本高昂，且严重依赖文本提示本身。如果提示不完美，搜索就会变成一场“徒劳无功的追逐 (wild-goose chase) ”。

核心概念: 嵌入的蝴蝶效应

Soft Reasoning 的作者提出了视角的转换。与其像温度参数那样操纵输出概率，为什么不操纵解法的输入表征呢？

假设很简单: 答案中生成的第一个 Token 决定了整个推理路径的轨迹。

如果我们能在高维嵌入空间中稍微微调那个第一个 Token 的“含义”，我们就能引导模型走向一条完全不同的、可能正确的推理路线。

第一步: 嵌入扰动 (Embedding Perturbation)

通常，LLM 使用贪婪解码根据提示 \(q\) 选择第一个 Token \(w^{(1)}\):

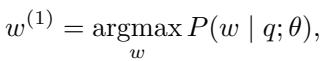
第一个 Token 贪婪选择的公式。

设 \(z\) 为这个被选中的 Token 的连续向量嵌入。Soft Reasoning 向这个嵌入添加少量的对角高斯噪声。模型不使用确切的嵌入 \(z\)，而是使用扰动版本 \(x_i\):

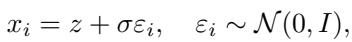
向嵌入添加高斯扰动的公式。

这里，\(\varepsilon_i\) 是随机噪声，\(\sigma\) 控制微调的强度。

关键在于, 只有第一个 Token 的嵌入受到了扰动。 一旦这个特定的、稍微偏移的“概念”被输入到模型中，序列的其余部分将使用贪婪搜索生成:

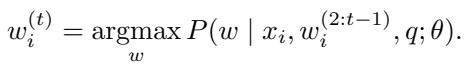
显示扰动输入后确定性生成的公式。

这是一个至关重要的区别。在标准的温度采样中，每一步都是随机的。在 Soft Reasoning 中，“种子” (扰动嵌入) 是随机的，但随后的生长 (文本生成) 是确定性的。这意味着每一个特定的噪声向量 \(x_i\) 都映射到一条唯一的、可重复的推理路径。

第二步: 软推理框架

既然我们可以通过微调嵌入来生成多样化的答案，我们就面临一个搜索问题。嵌入空间是无限的。我们去哪里寻找最佳答案？

我们将 LLM 视为一个“黑盒”函数，输入是扰动向量，输出是答案的质量。然后我们可以使用贝叶斯优化 (Bayesian Optimization, BO) 来寻找最佳扰动。

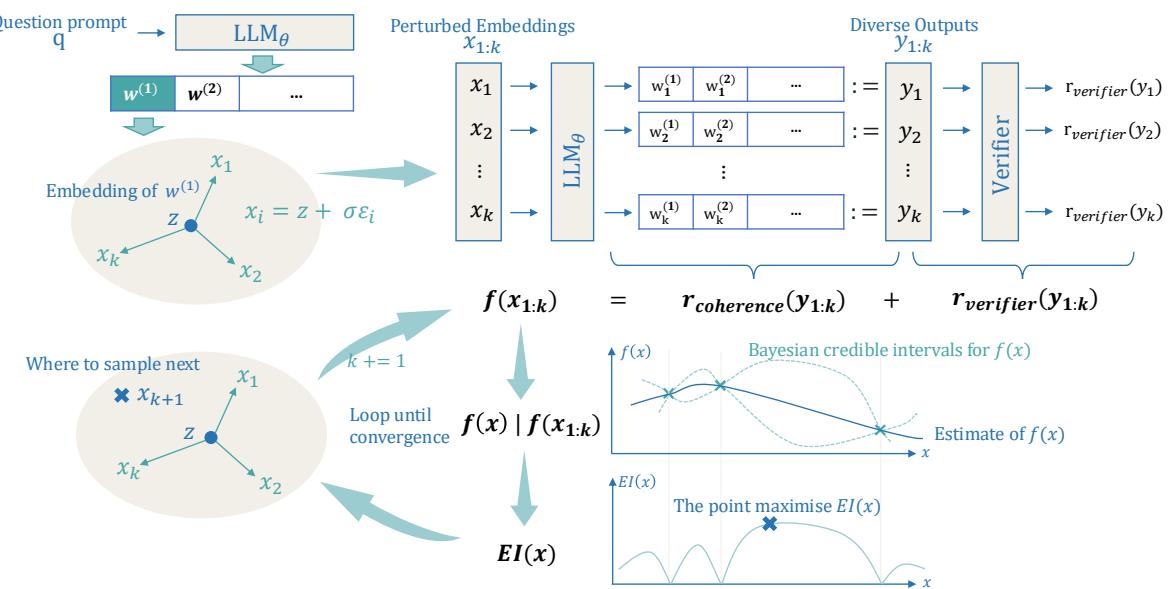
软推理框架概览，涉及扰动、验证和贝叶斯优化。

如图 2 所示，该过程在一个循环中工作:

  1. 扰动 (Perturb) : 生成一组候选嵌入 \(x_{1:k}\)。
  2. 生成 (Generate) : LLM 根据这些嵌入生成答案 \(y_{1:k}\)。
  3. 评估 (Evaluate) : 奖励函数对答案进行打分。
  4. 优化 (Optimize) : 贝叶斯模型观察这些分数并决定下一步搜索哪里。

第三步: 定义奖励

为了优化推理，我们需要从数学上定义什么样的答案是“好”的。作者定义了一个由两部分组成的目标函数 \(f(x)\):

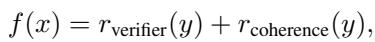
结合验证器和连贯性得分的目标函数公式。

1. 验证器 (\(r_{\text{verifier}}\)) : 这用于检查答案是否正确。在这个框架中，作者简单地使用 LLM 本身 (或另一个模型) 来验证结果。

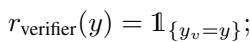
验证器得分的公式。

2. 连贯性 (\(r_{\text{coherence}}\)) : 如果我们对嵌入扰动过大，模型可能会生成无意义的内容。连贯性得分通过检查生成的 Token 的概率来确保文本的流畅性。

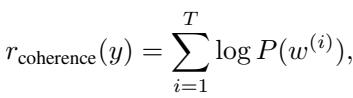
基于对数概率的连贯性得分公式。

这种结合确保了优化过程寻找的答案既在事实上正确 (根据验证器) ，在语言上也是合理的。

第四步: 贝叶斯优化与期望提升

这是该方法的亮点所在。随机尝试扰动是低效的。贝叶斯优化建立了一个概率模型 (代理模型) ，用于映射嵌入空间与奖励之间的关系。

它假设函数 \(f(x)\) 服从高斯过程。这使得系统可以预测嵌入空间中任意点的平均奖励 \(\mu\) 和不确定性 \(\sigma\)。

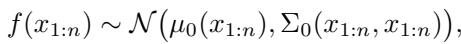
显示函数 f 的高斯过程假设的公式。

在观察了一些样本后，模型更新其信念:

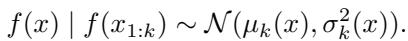
后验分布更新的公式。

为了决定下一步在哪里采样，算法使用了一种称为期望提升 (Expected Improvement, EI) 的采集函数。

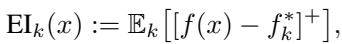
定义期望提升的公式。

简单来说，EI 平衡了探索 (Exploration) (寻找不确定性 \(\sigma\) 高的区域) 和利用 (Exploitation) (寻找预测奖励 \(\mu\) 高的区域) 。它提出的问题是: “与我们目前找到的最佳结果相比，我们期望这个新点能好多少？”

其闭式解的计算效率很高:

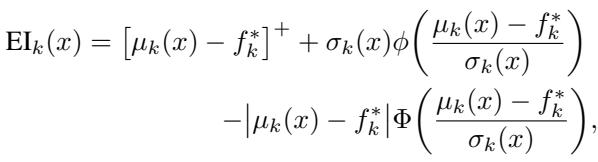
计算期望提升的闭式解公式。

通过最大化这个值，Soft Reasoning 能够智能地在嵌入空间中导航，收敛到能产生正确答案的“关键神经元”和表征上。

实验结果

研究人员在 GSM8K (数学) 和 StrategyQA (常识推理) 等高难度基准测试上，将 Soft Reasoning 与几个强基线进行了对比，包括自洽性 (Self-Consistency, SC) 和基于规划的方法如 RAP。

准确率

结果令人印象深刻。如下面的表 1 所示，Soft Reasoning 始终优于标准解码和自洽性方法，特别是在模型没有示例可依的零样本 (zero-shot) 设置中。

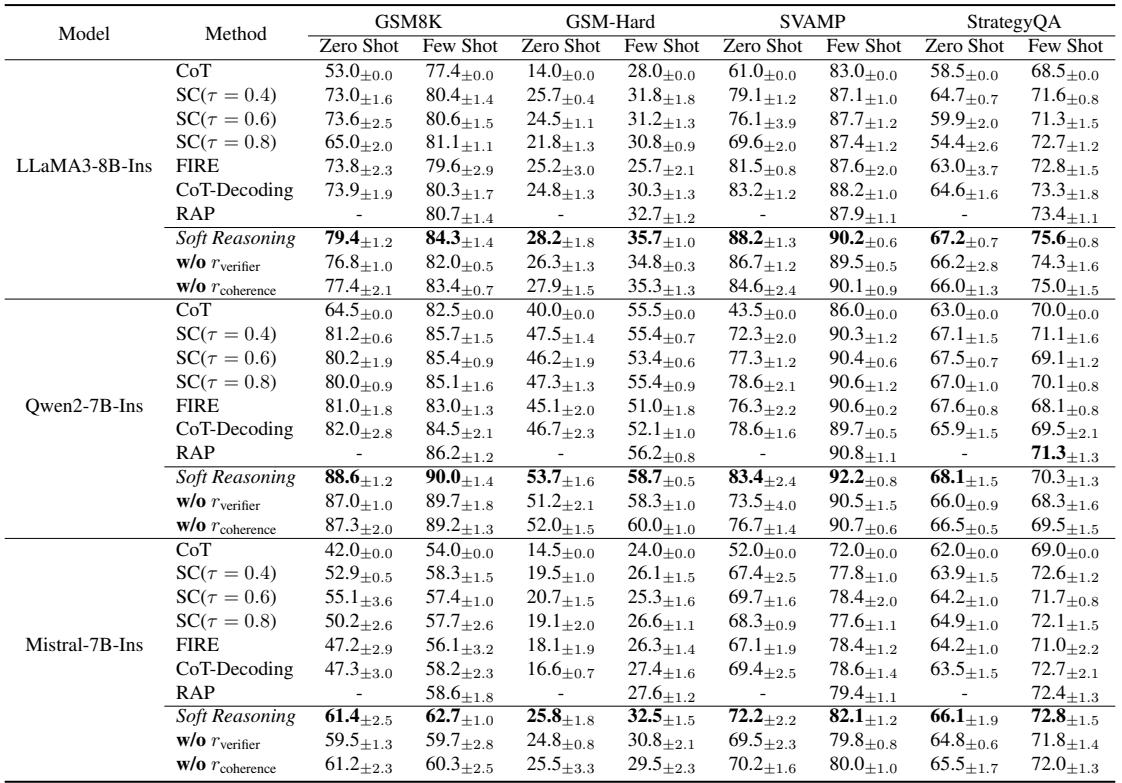
表 1. 不同推理方法在所有基准测试上的准确率(%)表现。

例如，在使用 LLaMA-3-8B 的 GSM8K 数据集上，Soft Reasoning 在零样本设置下达到了 79.4% 的准确率，而自洽性 (\(\tau=0.4\)) 仅为 73.0% 。 这本质上是从相同的模型参数中榨取了更多的推理能力。

效率

对“思维树”或其他规划算法最大的批评之一是它们速度慢且消耗大量 Token。它们会生成数以千计的中间想法。

Soft Reasoning 则轻量得多。因为它只对单个 Token 的嵌入进行操作，并使用高效的数学优化器，所以它大幅降低了计算开销。

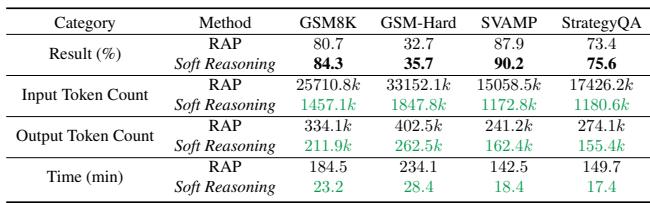
表 3. 本文方法与 RAP 在各基准测试上的性能和 Token 使用量对比。

表 3 突显了这种效率差距。与 RAP (一种树搜索方法) 相比，Soft Reasoning 仅使用了约 6% 的输入 Token , 且运行速度快了近 8 倍 (测试集耗时 23 分钟 vs. 184 分钟) ，同时还实现了更高的准确率 (84.3% vs 80.7%) 。

收敛性

贝叶斯优化真的学到了东西吗？还是只是运气好？

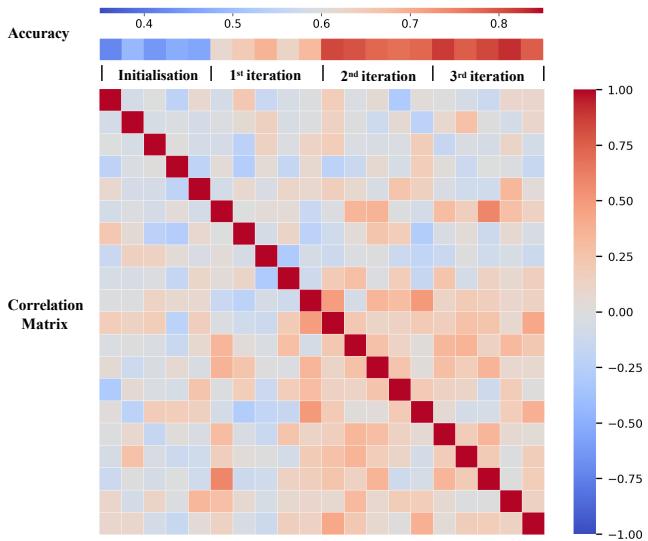
图 5. 贝叶斯优化迭代过程中相关矩阵演变的也是可视化。

图 5 展示了采样点之间的相关矩阵随迭代演变的情况。随着过程的继续，矩阵变得更有结构，表明算法正在识别嵌入空间中与高奖励相关的特定区域。它不是在瞎猜，而是在缩小搜索范围。

为什么它有效？神经学视角的解释

论文中最迷人的部分是对为什么扰动嵌入比温度采样更有效的分析。作者观察了 LLM 的 MLP (前馈) 层内神经元的激活率。

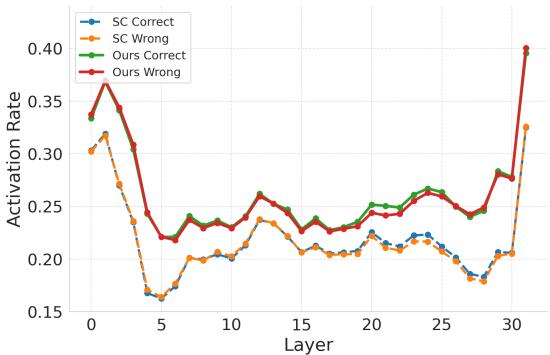
图 3. Transformer 层间的 MLP 层激活率。

图 3 比较了 Soft Reasoning (Ours) 与自洽性 (SC) 的神经元激活率。

  • SC (蓝色/橙色) : 激活率在中间层显著下降。
  • Soft Reasoning (绿色/红色) : 在各层之间保持了更稳定、更高的激活率。

这表明嵌入扰动触发了一组更广泛的神经通路。作者甚至识别出了“关键神经元”——那些与正确答案高度相关的特定神经元。

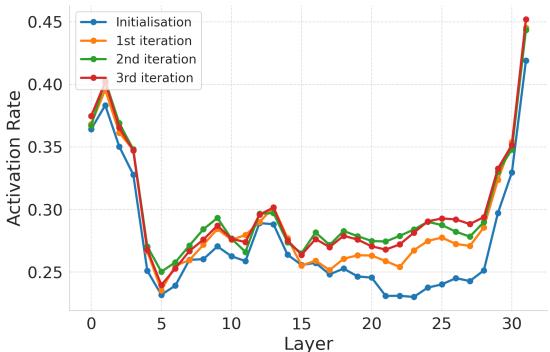
图 4. 关键 MLP 神经元在初始化和迭代期间跨 Transformer 层的激活率。

在图 4 中，我们可以看到随着贝叶斯优化的迭代 (从初始化到第 3 次迭代) ，这些关键神经元的激活率增加了 。 优化过程有效地“找到”了模型大脑中解决问题所需的部分，并强制其激活。

结论与启示

Soft Reasoning 代表了我们在与大语言模型交互方式上的一个复杂进步。这种方法不再将模型视为一个必须正确“提示”的刚性黑盒，或是一个必须随机“采样”的混乱黑盒，而是将模型的潜在空间视为一个待探索的景观。

通过结合嵌入的连续性与贝叶斯优化的严谨搜索能力，作者提供了一种具备以下特点的方法:

  1. 模型无关 (Model-Agnostic) : 无需重新训练 LLM 即可工作。
  2. 高效 (Efficient) : 比树搜索方法需要的 Token 少得多。
  3. 有效 (Effective) : 激活了标准解码所遗漏的关键推理通路。

对于学生和研究人员来说，这凸显了一个令人兴奋的方向: 潜空间优化 (Latent Space Optimization) 。 随着模型变得越来越大且难以重新训练，像 Soft Reasoning 这样在推理阶段优化输入和内部状态的技术，可能会成为解决复杂推理任务的标准配置。