利用概率实验设计驯服组合爆炸

想象一下，你是一位试图了解细胞工作原理的生物学家。你怀疑敲除特定基因会改变细胞的状态，也许能将癌细胞转化为良性细胞。你有 20 个不同的基因可以作为目标。

如果你一次测试一个基因，那是 20 次实验。这很容易管理。但生物学很少是线性的；基因之间存在相互作用。一个基因单独作用可能毫无反应，但如果与另一个基因配对，可能对细胞是致命的。为了充分理解这个系统，你需要测试各种组合。

问题就在这里: 组合爆炸 (The Combinatorial Explosion) 。

有 20 个基因，可能的组合数量 (即“全因子”设计) 是 \(2^{20}\)，这超过了一百万次实验。在湿实验室 (wet lab) 中，这是不可能的。你需要一种方法来运行可控数量的实验——比如 1,000 次——同时尽可能多地了解这些基因是如何相互作用的。

这正是 Divya Shyamal、Jiaqi Zhang 和 Caroline Uhler 的研究论文 “Probabilistic Factorial Experimental Design for Combinatorial Interventions” 所解决的问题。

在这篇文章中，我们将深入探讨他们提出的框架: 概率因子设计 (Probabilistic Factorial Design) 。 我们将探索为何给治疗分配概率 (剂量) ，而不是手工挑选组合，能提供一种可扩展且具有理论依据的方法，从而无需进行一百万次实验就能学习复杂的相互作用。

设计困境: 全因子 vs. 部分因子

在看新的解决方案之前，让我们先了解一下现状。

1. 全因子设计 (Full Factorial Design) : 你测试每一个可能的组合。

• *优点: * 获得所有相互作用的完美数据。
• *缺点: * 数学上无法扩展。实验数量随治疗数量 (\(p\)) 指数增长。

2. 部分因子设计 (Fractional Factorial Design) : 你选择特定的组合子集进行测试。

• *优点: * 使用的样本较少。
• *缺点: * 它很僵化。你需要仔细选择运行哪些组合以避免“混叠” (aliasing，即混淆不同的相互作用) 。如果设计错误，你可能会认为基因 A 和基因 B 在相互作用，而实际上是基因 C 在单独起作用。设计这些实验需要大量的先验假设 (例如，“我假设不存在 3 方式相互作用”) 。

本文作者提出了第三种方式，灵感来自于高通量生物筛选 (如 Perturb-seq) 的实际操作方式。他们建议采用概率方法，而不是明确选择“第 1 行接受基因 A 和 B”。

概率框架

核心思想简单而强大。实验者不是为某个单元 (如一个细胞) 分配固定的治疗组合，而是选择一个剂量 (dosage) 向量 \(\mathbf{d} = (d_1, \dots, d_p)\)。

每个 \(d_i\) 代表应用治疗 \(i\) 的概率。对于每个实验单元 \(m\)，治疗分配是基于这些概率随机抽取的。

在数学上，令 \(x_{m,i}\) 为治疗 \(i\) 在单元 \(m\) 上的干预状态。它的取值为 1 (应用治疗) 或 -1 (对照/未应用) 。

为什么要这样做？这一点非常巧妙:

• 如果你设置 \(\mathbf{d} \in \{0, 1\}^p\)，你就恢复了传统的确定性设计。
• 如果你设置 \(\mathbf{d} \in (0, 1)^p\)，你就创建了一个随机设计，随机探索组合空间。

通过调整连续参数 \(\mathbf{d}\)，实验者可以控制实验的“重心”，而无需明确枚举每一个组合。

组合结果建模

为了优化设计，我们需要一个世界的数学模型。输入 (治疗) 如何映射到输出 (结果) ？

作者将单元 \(m\) 的结果 \(y_m\) 定义为治疗向量 \(\mathbf{x}_m\) 的函数加上一些噪声:

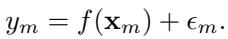
函数 \(f\) 可以是任何东西。然而，为了分析相互作用，作者使用了布尔函数的傅里叶展开 。 虽然“傅里叶”通常让我们想到正弦波，但在二进制输入 (\(\{-1, 1\}\)) 的背景下，傅里叶基函数仅仅是输入的乘积。

对于治疗的任意子集 \(S \subseteq [p]\)，基函数为:

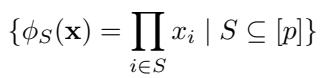
这看起来很抽象，让我们具体一点。

• 如果 \(S = \{1\}\)，那么 \(\phi_S(\mathbf{x}) = x_1\)。这测量了治疗 1 的主效应。
• 如果 \(S = \{1, 2\}\)，那么 \(\phi_S(\mathbf{x}) = x_1 x_2\)。这测量了治疗 1 和 2 之间的成对相互作用 。

任何函数 \(f\) 都可以写成这些相互作用的加权和:

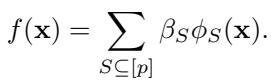
这里，\(\beta_S\) 代表集合 \(S\) 的相互作用强度。如果 \(\beta_{\{1,2\}}\) 很大，意味着基因 1 和 2 有很强的协同作用 (或拮抗作用) 。

与多项式模型的联系

这种傅里叶方法等同于统计学中常用的标准多项式响应面模型。如果你习惯看到像 \(\alpha_{ij} \mathbb{1}_{x_i=x_j=1}\) 这样的相互作用项，它们可以直接映射到傅里叶系数 \(\beta_S\)。

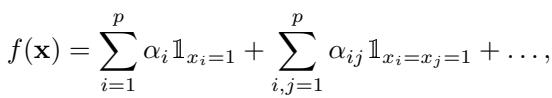
标准系数 (\(\alpha\)) 和傅里叶系数 (\(\beta\)) 之间的关系是线性的:

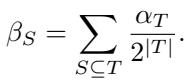
有界相互作用

在现实世界中，我们很少看到 10 个不同的基因以一种无法用低阶效应解释的独特方式同时相互作用。作者假设有界阶相互作用 (Bounded-order interactions) 。 我们假设相互作用仅存在于大小不超过 \(k\) 的范围内 (例如 \(k=2\) 或 \(k=3\)) 。

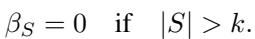
这个假设至关重要，因为它将我们需要估计的参数数量从 \(2^p\) 减少到 \(p\) 的多项式级别，使问题变得可解。

被动设置: “一劳永逸”策略

论文的第一个主要贡献解决了被动 (passive) 设置问题。你有 \(n\) 个样本的预算。你需要在开始时一次性选择剂量向量 \(\mathbf{d}\)。你应该选择什么剂量才能尽可能准确地估计模型系数 \(\boldsymbol{\beta}\)？

为了回答这个问题，我们看看估计量。我们希望从数据观察中恢复 \(\boldsymbol{\beta}\)。设计矩阵 \(\mathcal{X}\) 包含每个样本的傅里叶特征:

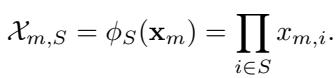
由于我们的设计是随机的，矩阵 \(\mathcal{X}\) 可能是病态的 (某些列可能偶然相关) 。为了处理这个问题，作者使用了截断普通最小二乘法 (Truncated Ordinary Least Squares, OLS) 估计量。本质上，它执行标准的线性回归，但如果矩阵太不稳定 (即特征值太小) ，它会“放弃” (返回零) 以避免巨大的方差。

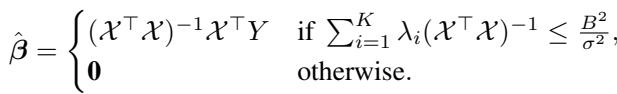
指标: 均方误差

我们希望最小化估计系数 \(\hat{\boldsymbol{\beta}}\) 和真实系数 \(\boldsymbol{\beta}\) 之间的预期均方误差 (MSE)。该误差的理论界限很大程度上取决于矩阵 \(\mathcal{X}^\top \mathcal{X}\) 的特征值 (\(\lambda_i\))。

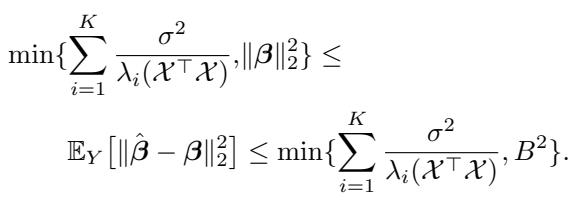
\(\sum \frac{1}{\lambda_i}\) 这一项是关键。在线性回归中，估计量的方差与逆协方差矩阵的迹成正比。 为了最小化误差，我们需要大的特征值。

最优策略

这是论文中一个惊人的结果。在概率设计框架下，对于任何相互作用阶数 \(k\):

最优剂量是 \(\mathbf{d} = (1/2, 1/2, \dots, 1/2)\)。

这意味着基本上就是为每个单元的每个治疗抛一枚公平的硬币。

为什么是 \(1/2\) 最优？ 这归结为总体协方差矩阵，记为 \(\Sigma(\mathbf{d})\)。该矩阵的元素由剂量决定:

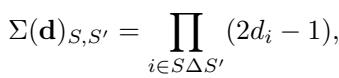
该矩阵的特征值决定了误差。无论 \(\mathbf{d}\) 如何，特征值之和是常数。根据调和平均数的性质 (柯西-施瓦茨不等式) ，当所有特征值相等时，逆特征值之和最小。

当 \(\mathbf{d} = 1/2\) 时，项 \((2d_i - 1)\) 变为 0。这将协方差矩阵 \(\Sigma(\mathbf{d})\) 坍缩为单位矩阵 。 单位矩阵的所有特征值都等于 1。这是回归的完美条件——这意味着你所有的特征 (相互作用) 彼此完全不相关。

作者证明剂量 1/2 在一个非常小的因子范围内是最优的:

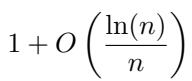
具体来说，误差率随样本量 \(n\) 衰减如下:

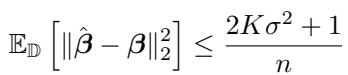
这意味着要估计一个 \(k\) 方式相互作用模型，你需要大约 \(O(k p^{3k} \ln p)\) 个样本。这是多项式级别的，而不是指数级别的，这对于可扩展性来说是一个巨大的胜利。

主动设置: 边做边学

在许多科学场景中，你不会一次性运行所有实验。你会运行一批，分析数据，然后设计下一批。这就是主动学习 (Active Learning) 。

假设我们已经进行了 \(T-1\) 轮实验。我们收集了数据矩阵 \(\mathcal{X}_1, \dots, \mathcal{X}_{T-1}\)。我们希望选择下一轮的剂量 \(\mathbf{d}_T\) 以最小化总误差。

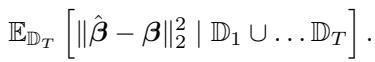
由于我们已经有了数据，我们当前的“信息”由前几轮的格拉姆矩阵 \(\mathcal{X}^\top \mathcal{X}\) 之和表示。我们可能偶然收集到了有偏差的数据，或者第一轮被迫使用了次优剂量。第 \(T\) 轮是我们“修正”协方差结构的机会。

作者推导了一个近似最优的采集函数。我们选择剂量 \(\mathbf{d}_T\) 来最小化合并后协方差 (过去的数据 + 预期的新数据) 的逆特征值:

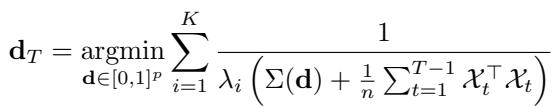
这个公式不能像被动设置那样有闭式解，但它是 \(\mathbf{d}\) 的平滑函数。这意味着我们可以使用数值优化 (如梯度下降或 SLSQP) 来找到下一轮的最佳剂量。

这是一个强大的工具。它允许实验动态地“填补”信息空间中的漏洞。

扩展: 现实世界的约束

论文将此框架扩展到了几个实际场景。

1. 供应有限

如果试剂昂贵，或者同时应用过多治疗会杀死细胞怎么办？我们可能会施加一个约束，即剂量之和不能超过限制 \(L\):

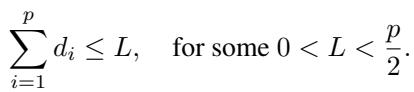
对于简单的加性模型 (\(k=1\)) ，作者证明最优策略是平均分配预算，即对所有治疗设置 \(d_i = L/p\)。对于高阶相互作用，数值优化器 (来自主动设置) 可以遵守此约束并找到最佳解。

2. 异方差噪声

如果不同轮次的实验具有不同的噪声水平 (\(\sigma_t^2\)) 怎么办？也许实验室设备重新校准了，或者使用了不同批次的细胞。优化函数通过按精度 (\(1/\sigma^2\)) 加权协方差矩阵来自然适应这种情况:

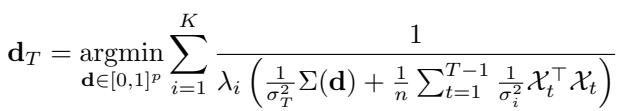
3. 模拟目标分布

有时，你不只是想最小化回归误差。你可能希望你的实验群体模仿自然界中发现的特定组合分布 \(q\)。

作者表明，通过最小化目标分布 \(q\) 与设计分布 \(p_{\mathbf{d}}\) 之间的 KL 散度，最优剂量仅仅是目标分布的边缘概率。

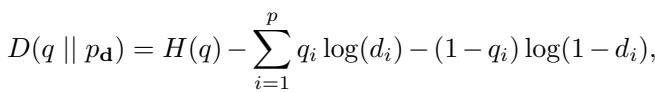
实验验证

理论听起来很可靠，但在实践中有效吗？作者进行了模拟来验证他们的主张。

模拟 1: 1/2 真的是最优的吗？

在这个实验中，他们固定了一个“真实”模型，并尝试使用不同的剂量向量来估计它。他们改变了剂量向量与理论最优值 \(0.5\) 的距离。

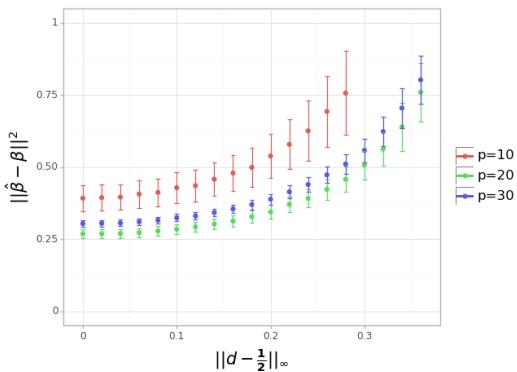
解释: 看图 1。x 轴表示与剂量 0.5 的距离。y 轴是估计误差。当你远离 0.5 时，曲线明显上升。这从经验上证实了定理: “公平抛硬币” (0.5) 能最小化误差。

模拟 2: 均匀剂量

他们还测试了将所有剂量设置为相同的值 \(d\)，将 \(d\) 从 0.4 变化到 0.6。

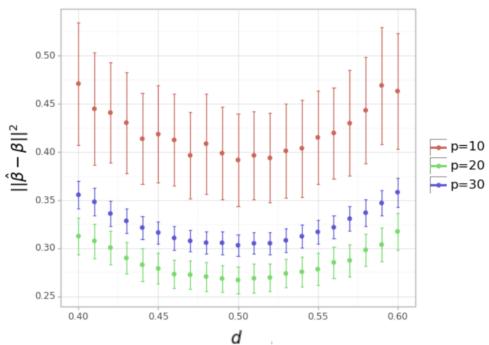
解释: 图 2 显示了一个清晰的“U”形，中心正好在 0.5。即使稍微偏离 (例如到 0.4 或 0.6) 也会增加误差，加强了被动设置中半剂量策略的敏感性和最优性。

模拟 3: 主动 vs. 随机

在这里，他们比较了主动 (Active) 策略 (每轮优化剂量) 与随机 (Random) 策略 (选择随机剂量) 以及固定的半剂量 (Half) 策略。

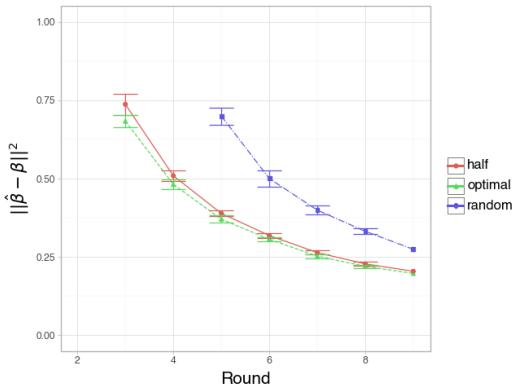
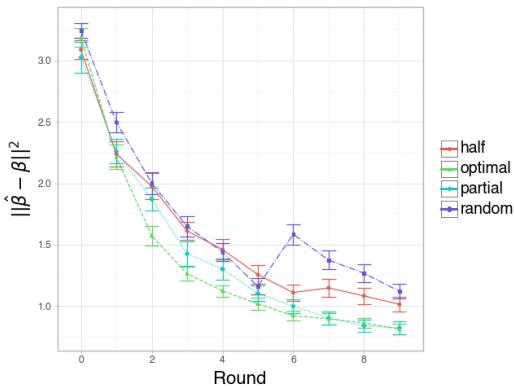
解释:

• 图 3 (大 \(N\)) : 有了足够的样本，“半剂量”策略 (红色) 和“最优”主动策略 (绿色) 表现同样出色，都击败了随机策略 (蓝色) 。这说得通；如果你有足够的数据，被动最优策略很难被击败。
• 图 4 (小 \(N\)，高噪声) : 这是有趣的情况。当数据稀缺时, 最优策略 (绿色) 在早期轮次中明显优于其他策略。这表明当实验昂贵 (样本量小) 时，使用主动学习框架计算精确的最优剂量具有显著优势。

模拟 4: 约束优化

最后，他们测试了剂量总和受限的有限供应场景。

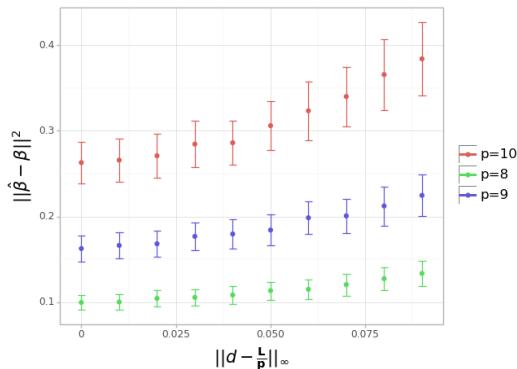
解释: 随着剂量偏离可用预算的均匀分布 (\(L/p\))，误差增加。这证实了即使在约束条件下，平均分配资源通常也是学习相互作用的最佳起始策略。

结论与关键要点

论文 “Probabilistic Factorial Experimental Design for Combinatorial Interventions” 为困扰许多实验科学的问题提供了一个严谨的数学基础: 如何在不测试所有内容的情况下研究复杂的组合。

关键要点:

1. 概率设计: 从离散的组合选择转向连续的“剂量”，使设计问题变得可微分且可扩展。
2. 1/2 的力量: 在被动 (一次性) 实验中，将每个治疗概率设置为 50% 对于学习任何阶数的相互作用在理论上都是近似最优的。它使特征不相关。
3. 主动修正: 如果分轮进行实验，你可以数值优化剂量以修正过去的不平衡或约束，这在样本量较小时特别有价值。
4. 灵活性: 该框架自然地处理约束 (预算限制) 和实验噪声的变化。

对于学生和研究人员来说，这项工作弥合了经典实验设计 (可能过于僵化) 与现代高通量能力之间的差距。它表明，有时理解复杂确定性系统的最佳方法是用随机性去探索它。