引言

在安全关键型人工智能 (AI) 领域——想想自动驾驶、医疗诊断或飞行控制系统——“还不错”是不够的。我们需要保证。我们需要确切地知道，如果一个停车标志稍微旋转了一点或者上面贴了一张贴纸，汽车的神经网络不会将其误分类为限速标志。

这就是 神经网络验证 (Neural Network Verification) 的领域。其目标是从数学上证明，对于给定的一组输入 (即“扰动集合”) ，网络将 始终 产生正确的输出。

从历史上看，研究人员一直处于进退两难的境地:

  1. 线性边界传播 (Linear Bound Propagation, LBP) : 像 CROWN 或 \(\alpha\)-CROWN 这样的方法速度极快，可以扩展到大规模网络。然而，它们可能很“松散”，这意味着它们可能会无法验证一个安全的网络，因为它们的数学近似过于保守。
  2. 半正定规划 (Semidefinite Programming, SDP) : 这些方法提供了更紧密、更精确的边界。缺点是什么？它们极其缓慢。它们的计算复杂度呈立方级增长 (\(O(n^3)\)) ，这使得它们无法应用于现代的大规模深度学习模型。

SDP-CROWN 应运而生。

在伊利诺伊大学厄巴纳-香槟分校的一篇新论文中，研究人员提出了一个混合框架来弥补这一差距。通过巧妙地利用半正定规划的原理推导出一类新型的线性边界，他们在保持边界传播速度的同时，实现了 SDP 的紧密度。

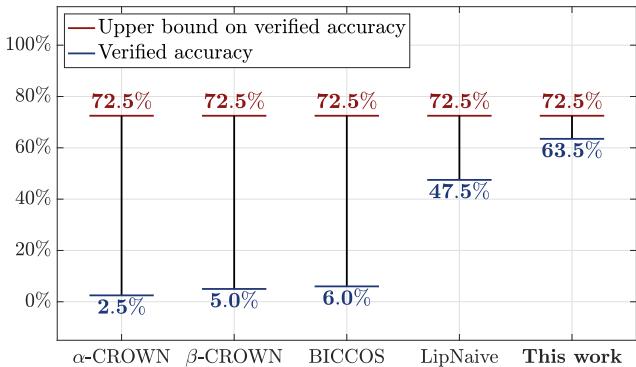
图 1: 在 CIFAR-10 数据集上对 ConvLarge 网络进行验证。验证准确率的比较显示 SDP-CROWN 显著优于最先进的方法。

如图 1 所示，这种差异并非微不足道。在大型卷积网络上，传统的快速验证器针对 \(\ell_2\) 攻击仅能达到 2.5% 到 6.0% 的验证准确率，而 SDP-CROWN 达到了惊人的 63.5% , 逼近理论上限。

在这篇文章中，我们将拆解这篇论文的数学原理，解释为什么传统方法难以应对特定类型的攻击，以及 SDP-CROWN 如何通过每层仅增加一个参数来解决这个问题。

背景: 我们在验证什么？

在深入解决方案之前，让我们先定义问题。我们将神经网络 \(f(x)\) 视为一系列线性变换 (权重 \(W\)) 和非线性激活函数 (ReLU) 。

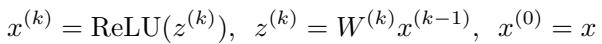
递归定义带有 ReLU 激活函数的神经网络的方程。

我们要确保对于输入 \(\hat{x}\) (例如，一张熊猫的图片) ，任何在一定距离内的对抗样本 \(x\) 仍被正确分类。如果正确的类别是 \(i\)，那么类别 \(i\) 的得分必须大于任何错误类别 \(j\) 的得分。在数学上，我们要找到最小的安全“裕度 (margin) ”:

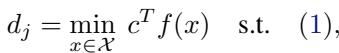
鲁棒性裕度 d_j 的方程。

如果 \(d_j\) 为正，我们就是安全的。如果它是负的，则存在攻击。

攻击的几何形状: 盒子与球体

输入周围“危险区域”的形状至关重要。

  1. \(\ell_\infty\) 范数 (盒子) : 这假设每个像素可以独立改变一个很小的量 \(\epsilon\)。在几何上，这是一个超矩形 (或盒子) 。
  2. \(\ell_2\) 范数 (球体) : 这假设变化的总欧几里得距离受限于 \(\rho\)。在几何上，这是一个超球体 (或球体) 。

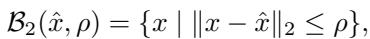
定义 L2 范数球体约束的方程。

虽然边界传播方法 (如 \(\alpha\)-CROWN) 在处理“盒子”扰动方面非常出色，但它们在处理“球体” (\(\ell_2\)) 扰动方面却出名地糟糕。

问题: 为什么边界传播对 \(\ell_2\) 很松散？

线性边界传播 (LBP) 的工作原理是将线性约束逐层推过网络。它是为处理单个特征而设计的。当你要求 LBP 验证器处理一个 \(\ell_2\) 球体时，它不知道如何处理球体的曲率。

为了使数学运算可行，标准的 LBP 方法本质上是将球体包裹在一个尽可能紧密的盒子 (\(\ell_\infty\) 盒子) 中，然后验证那个盒子。

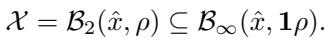
显示将 L2 球体松弛为 L-infinity 盒子的方程。

这看起来像是一个无害的近似，但在高维空间中，这是灾难性的。

  • 半径为 \(\rho\) 的球体包含在边长为 \(2\rho\) 的盒子中。
  • 然而，该盒子的角实际上距离中心 \(\sqrt{n}\rho\)。

在一个高维网络中 (\(n\) 很大) ，盒子的体积远大于球体。你实际上是在要求验证器保证一个比实际攻击空间大 \(\sqrt{n}\) 倍的空间的安全性。这导致了过于保守的结果——验证器会说“我不能保证这是安全的”，即使它实际上是安全的。

解决方案: SDP-CROWN

研究人员提出了一种方法，可以捕捉 \(\ell_2\) 约束的曲率，而不会产生全量 SDP 求解器的巨大计算成本。

核心概念

标准的边界传播为网络输出寻找线性下界和上界:

\[ c^T f(x) \geq g^T x + h \]

这里，\(g\) 是斜率，\(h\) 是偏移量 (偏置) 。

SDP-CROWN 保留了传播这些线性边界的高效结构，但以一种更聪明的方式计算偏移量 \(h\)。它不再使用盒子来计算 \(h\)，而是求解一个源自半正定规划的专门优化问题。

第一步: 原问题 (The Primal Problem)

为了在 \(\ell_2\) 球体内为给定的斜率 \(g\) 找到尽可能紧密的偏移量 \(h\)，理论上我们需要求解这个最小化问题:

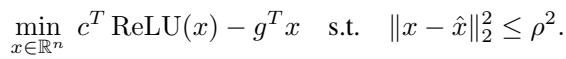
带有 L2 约束的 ReLU 网络上线性函数的最小化问题。

这看起来很简单，但 \(\text{ReLU}(x)\) 项使其成为非凸的，难以精确求解。

第二步: SDP 松弛 (The SDP Relaxation)

为了解决这个问题，作者采用了鲁棒控制理论中的一个经典技巧: SDP 松弛 。 他们不将 ReLU 约束 \(x = \text{ReLU}(z)\) 视为硬性的非线性，而是将其视为二次约束。

如果 \(x = \text{ReLU}(z)\)，我们可以将变量分为正部和负部 (\(u\) 和 \(v\)) ，使得 \(u \geq 0, v \geq 0\) 且它们的乘积为零 (\(u \odot v = 0\)) 。

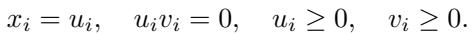
显示 ReLU 约束变量拆分的方程。

通过将约束 \(u \odot v = 0\) (这是难点) 松弛为半正定矩阵约束，他们获得了一个凸问题。这也是标准 SDP 方法止步的地方——他们将这个巨大的矩阵扔进求解器，这需要 \(O(n^3)\) 的时间。

第三步: 高效对偶 (The Efficient Dual)

这是论文的主要贡献。研究人员没有停留在矩阵公式上。他们推导了这个特定 SDP 松弛的 拉格朗日对偶 (Lagrangian dual) 。

通过解析推导数学公式，他们意识到对于这种特定的结构，巨大的矩阵优化问题塌缩成了一个只需要优化 每层一个标量变量 的问题，记为 \(\lambda\)。

最终的边界在 定理 4.1 中阐述:

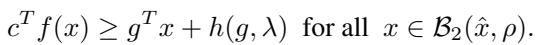
显示 SDP-CROWN 推导出的线性下界的方程。

其中偏移量 \(h(g, \lambda)\) 定义为:

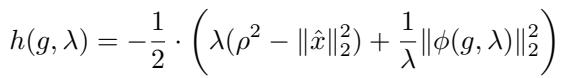
SDP-CROWN 中偏移量函数 h(g, lambda) 的方程。

而 \(\phi\) 是一个特定的向量函数:

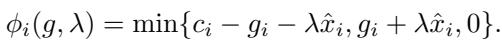
偏移量计算中使用的 phi 函数的定义。

为什么这很重要？

  1. 复杂度: 我们不再是在解一个矩阵问题。我们正在最大化一个关于标量 \(\lambda \geq 0\) 的函数。这既便宜又快。
  2. 兼容性: 这个 \(h(g, \lambda)\) 的计算可以直接替换到现有的边界传播工具中，如 \(\alpha\)-CROWN。你只需将“基于盒子”的偏移量计算替换为这个“基于 SDP”的计算。

可视化改进

为了理解为什么这个数学推导很重要，我们要看看松弛的几何形状。论文提供了一个简单的 2 神经元案例中标准方法与 SDP-CROWN 产生的边界的可视化。

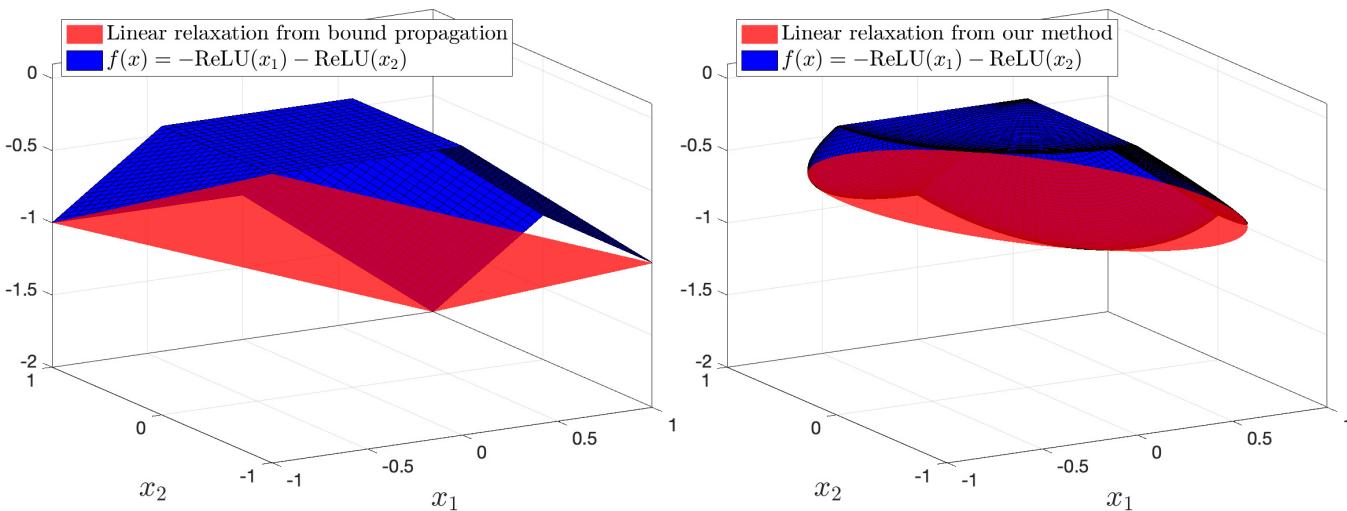
图 2: 线性松弛的比较。左图: 边界传播使用盒子，产生了松散、尖锐的松弛。右图: SDP-CROWN 使用球体，产生了平滑、紧密的包络。

  • 左图 (标准 LBP) : 松弛是尖锐且有棱角的。它是针对盒子优化的，所以当应用于球体时，它在边界和真实函数之间留下了巨大的空隙 (松散) 。
  • 右图 (SDP-CROWN) : 松弛是平滑的，并且紧贴函数表面。这种形状来自于通过 \(\lambda\) 参数隐式处理 \(\ell_2\) 约束。

作者在理论上证明，当扰动以零为中心时，SDP-CROWN 确实比标准边界传播 紧密 \(\sqrt{n}\) 倍 。

实验与结果

理论听起来很棒，但在真实网络上效果如何？作者在 MNIST 和 CIFAR-10 模型上测试了 SDP-CROWN，并与以下方法进行了比较:

  • \(\alpha\)-CROWN / \(\beta\)-CROWN: 最先进的边界传播方法。
  • LipNaive / LipSDP: 基于 Lipschitz 常数的方法。
  • LP-All / BM-Full: 纯凸松弛方法 (非常慢) 。

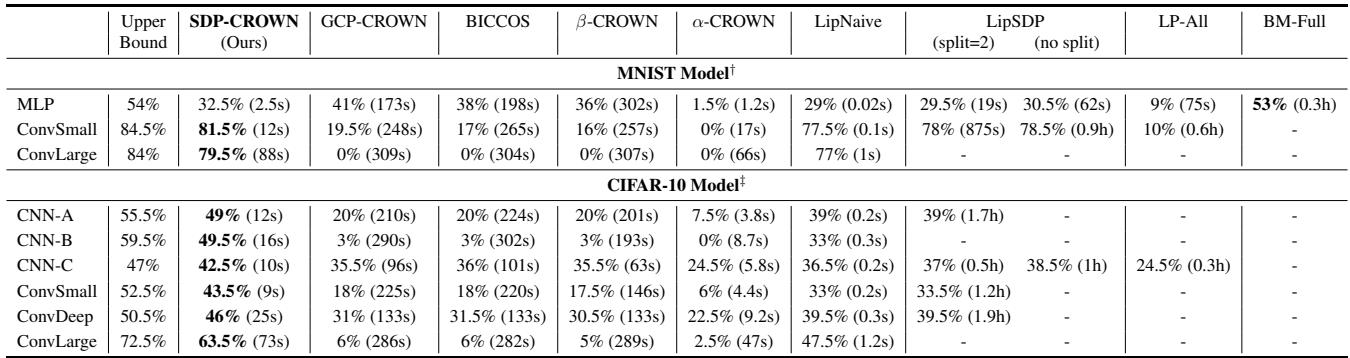
验证准确率

参考 表 1 (在下面的图像集中部分可见) ，结果是一致的。在 ConvLarge 模型 (CIFAR-10) 上，该模型拥有约 247 万个参数和 6.5 万个神经元:

方法验证准确率时间
\(\alpha\)-CROWN2.5%47s
LipNaive47.5%1.2s
SDP-CROWN (Ours)63.5%73s

传统的边界传播完全崩溃了 (2.5%) 。朴素的 Lipschitz 方法很快但很松散。SDP-CROWN 在实现了高认证率的同时，仅比快速方法多花了一点时间 (73秒 vs 47秒) 。

表 1: 显示 SDP-CROWN 卓越性能的 L2 范数扰动下的验证准确率。

下界的紧密度

查看原始边界也很有启发性。在验证中，我们希望正确类别的得分下界保持在 0 以上。

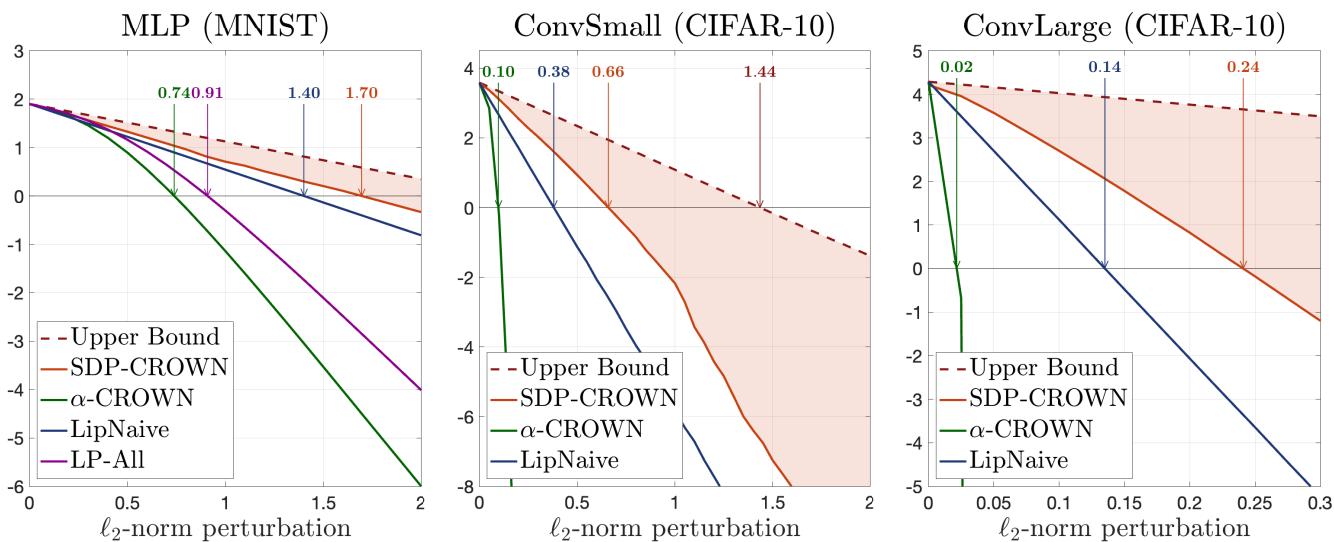
图 3: 鲁棒性裕度的下界。SDP-CROWN (红线) 在更大的扰动下仍保持为正，优于其他方法。

在图 3 中，x 轴代表攻击的大小 (\(\ell_2\) 半径) 。随着攻击变强，认证的下界会下降。

  • 蓝线 (\(\alpha\)-CROWN): 对于较大的模型，几乎立即跌破零点。
  • 红线 (SDP-CROWN): 更紧密地贴合上界 (黑线) ，并在更大的扰动半径下保持为正。

结论

SDP-CROWN 代表了神经网络形式化验证迈出的重要一步。它成功地找出了当前方法效率低下的根本原因——基于盒子的验证工具与基于球体 (\(\ell_2\)) 的对抗性攻击之间的不匹配。

通过回到数学绘图板，利用半正定规划松弛的对偶性，作者推导出了一个公式，它是:

  1. 紧密的: 捕捉了攻击的真实几何形状。
  2. 高效的: 每层仅增加一个参数，而不是一个 \(n \times n\) 矩阵。
  3. 可扩展的: 能够验证拥有数百万参数的网络。

对于鲁棒人工智能的学生和从业者来说，这篇论文强调了一个宝贵的教训: 有时加速算法的最佳方法不是更好的代码，而是更好的数学。通过在编写一行代码之前解析地解决优化中昂贵的部分，研究人员将一个棘手的问题变成了一个可计算的问题。