引言

在生物系统中，忽略无关信息的能力与处理相关信息的能力同等重要。当你身处一个嘈杂的鸡尾酒会时，你的耳朵会接收来自四面八方的声波——玻璃杯的碰撞声、背景音乐以及十几个重叠的对话声。然而，你的大脑却能展现出惊人的过滤能力: 它能衰减噪声并放大你试图进行的那个单一对话。这种选择性注意对于在一个复杂、数据丰富的世界中生存至关重要。

人工自主系统，例如使用强化学习 (RL) 的机器人或计算机视觉模型，也面临着完全相同的挑战。它们被感官输入狂轰滥炸。现代 Transformer 架构将这些输入作为一组向量 (Token) 进行处理。然而，在处理流程的末端，系统通常需要做出一个单一的决策: 左转、归类为“猫” 或 抓取物体。这需要将大量的输出嵌入 (Embeddings) 压缩成一个单一的、可操作的表示。

这个过程被称为 池化 (Pooling) 。

在视觉或强化学习等非序列任务中，从业者通常采用标准方法: 平均池化 (Average Pooling) (取所有输出的平均值) 、最大池化 (Max Pooling) (取最大值) 或使用学习到的 类别标记 (Class Token, CLS) 。 这些通常被视为随意的设计选择。

然而，最近的研究表明，这些标准选择是脆弱的。当输入中有用的“信号”与无关的“噪声”之比发生变化时，它们会发生灾难性的失效。

在这篇文章中，我们将深入探讨论文《Robust Noise Attenuation via Adaptive Pooling of Transformer Outputs》。我们将探索为什么标准池化方法在数学上注定会在变噪条件下失效，以及 自适应池化 (AdaPool) ——一种基于注意力的聚合机制——如何为自主系统提供理论上鲁棒的解决方案。

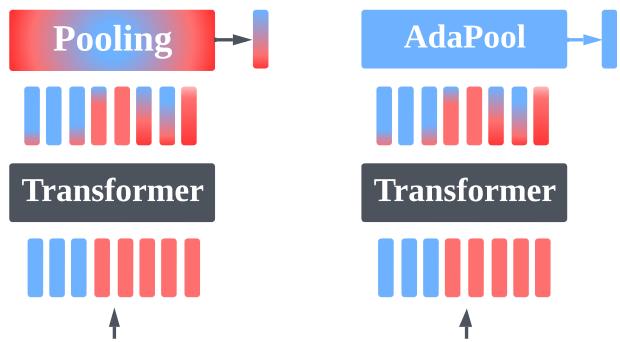
问题所在: 将池化视为矢量量化

要理解池化为何重要，我们必须重新审视它。它不仅仅是一个降维步骤；它是一个压缩问题。

考虑一个输入向量集合 \(\mathbf{X}\)。在任何给定的场景中，这些向量的一个子集包含与任务相关的信息 (信号，\(\mathbf{X}_s\)) ，其余的则是干扰项 (噪声，\(\mathbf{X}_\eta\)) 。

• 信号 (\(k\) 个向量): 影响正确输出的实体或像素。
• 噪声 (\(N-k\) 个向量): 背景景色、无关的智能体或静电干扰。
• SNR: 信噪比定义为 \(k/N\)。

全局池化方法的目标是将集合 \(\mathbf{X}\) 压缩成单个向量 \(\mathbf{x}_c\)，在尽可能保留信号的同时丢弃噪声。我们可以将池化函数 \(C(\mathbf{X})\) 一般性地定义为输入的加权和:

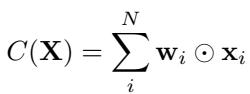
这里，\(\mathbf{w}_i\) 代表分配给每个输入向量的权重。

定义失效: 信号损失

我们如何衡量一种池化方法是否有效？我们要借鉴矢量量化 (Vector Quantization, VQ) 中的概念。在 VQ 中，一组点的“最佳”压缩是它们的 质心 (算术平均值) 。因此，我们输入的最佳表示是 信号 向量的质心，完全忽略噪声向量。

我们将 信号损失 (\(\mathbb{L}\)) 定义为我们的池化输出 \(\mathbf{x}_c\) 与真实信号向量之间的均方误差 (MSE):

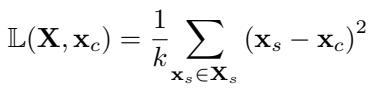
数学目标很简单: 最小化信号损失。 为了实现零信号损失，池化方法必须完美地分配权重:

1. 对每个信号向量分配统一的权重 (\(\frac{1}{k}\))。
2. 对每个噪声向量分配零权重 (\(0\))。

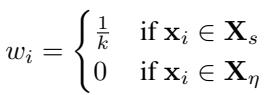
如果池化方法偏离了这种权重分布，就会引入干扰。正如我们将看到的，标准方法几乎总是会偏离。

标准池化的脆弱性

该论文对为什么平均池化和最大池化不足以支持鲁棒系统提供了严格的分析。它们拥有“归纳偏置”，仅在极端、特定的场景下有效。

1. 全局平均池化 (AvgPool)

AvgPool 是许多非序列 Transformer 任务的默认选择。它计算所有输出向量的平均值。

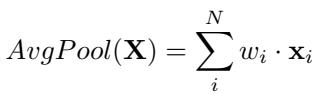
隐式地，这给每个向量分配了 \(1/N\) 的权重，而不考虑其内容。

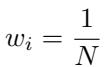
AvgPool 何时有效？

AvgPool 仅在两种罕见情况下是最佳的:

1. 无噪声: 输入集合是纯信号 (\(\mathbf{X}_\eta = \emptyset\))。
2. 相同分布: 噪声向量的平均值恰好与信号向量的平均值完全相同。

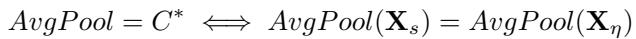
失效模式

实际上，信号和噪声很少是同分布的。如果你试图在雾蒙蒙的田野 (噪声) 中识别一个行人 (信号) ，雾的“平均值”并不等同于人的“平均值”。

随着噪声数量 (\(N\)) 增加而信号 (\(k\)) 保持不变，AvgPool 会稀释信号表示。分配给信号的权重 (\(1/N\)) 向零收缩，而噪声的总权重则增加。 AvgPool 在低信噪比 (SNR) 机制下会崩溃。

2. 全局最大池化 (MaxPool)

MaxPool 取每个向量在特征维度上的最大值。

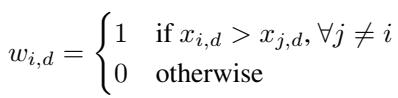
MaxPool 何时有效？

MaxPool 极具选择性。它实际上给在特定特征维度上具有最大值的向量分配权重 1，给其他所有向量分配权重 0。只有在恰好有 一个 信号向量 (\(k=1\)) 且该向量在每个特征上都包含最大值时，它才是最佳的。

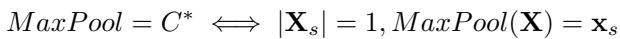
失效模式

MaxPool 假设了一种“赢家通吃”的场景。如果你有多个需要聚合以形成完整画面的信号向量 (例如，三个智能体协作抬起一个箱子) ，MaxPool 将只选取它们中最极端的特征，可能会破坏关系信息。MaxPool 倾向于在信号非常稀疏 (大海捞针) 时表现良好，但在信号复杂且分布广泛时会失效。

解决方案: 自适应池化 (AdaPool)

如果说 AvgPool 过于民主 (每个人都有投票权) ，而 MaxPool 过于独裁 (只有声音最大的才算数) ，那么我们需要一种能够根据向量内容 调整 其投票系统的方法。

作者建议使用注意力机制本身作为池化层。这被称为 AdaPool 。

AdaPool 如何工作

AdaPool 使用标准的键-查询-值 (Key-Query-Value, KQV) 注意力机制，但设置特定:

1. 输入: 向量集合 \(\mathbf{X}\) 作为键 (Keys) 和值 (Values)。
2. 查询: 选择单个查询向量 \(\mathbf{x}_q\) (稍后详细介绍) 。
3. 核函数: 一个关系函数 (点积) 测量查询与每个输入向量之间的相似度。

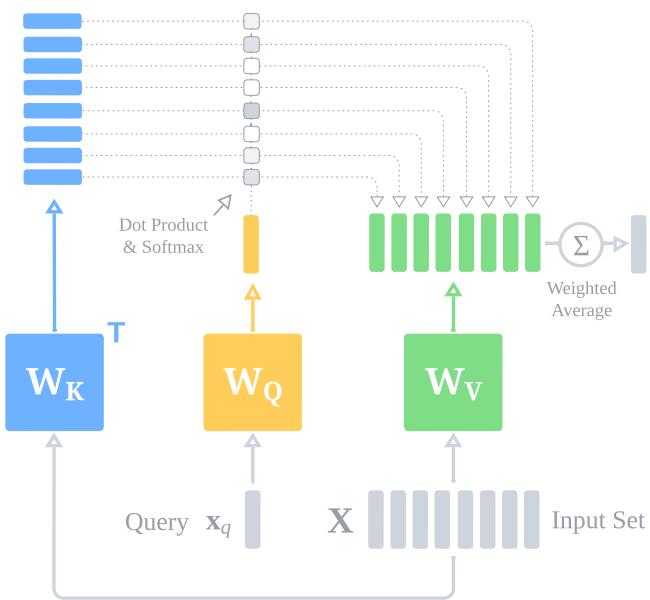
注意力分数决定了权重。Softmax 函数对这些分数进行归一化，确保它们的和为 1。

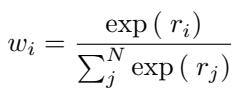
池化的统一理论

该论文最优雅的理论贡献之一是证明了 AvgPool 和 MaxPool 只是 AdaPool 的特例。

• AvgPool 是具有零核函数的 AdaPool: 如果查询和键的权重是零矩阵，则点积变为零。\(\exp(0) = 1\)。Softmax 将 1 除以 \(N\)，产生 \(1/N\) 的权重——与平均池化完全相同。
• MaxPool 是极限状态下的 AdaPool: 如果我们用温度参数 \(\beta\) 缩放注意力分数，当 \(\beta \to \infty\) 时，Softmax 函数变成“硬”最大值 (hard max)，将所有权重分配给点积最高的向量。

这表明 AdaPool 涵盖了整个池化行为谱系。通过学习权重 \(W_Q\) 和 \(W_K\)，网络可以根据当前输入的信噪比，学习 表现得像 AvgPool、MaxPool 或介于两者之间的任何形式。

鲁棒性的数学原理

为什么 AdaPool 更鲁棒？归根结底在于 边际 (Margin) 。

为了近似最佳量化器 (信号权重为 \(1/k\)，噪声权重为 \(0\)) ，注意力机制必须在信号向量的关系分数 (\(r_s\)) 和噪声向量的关系分数 (\(r_\eta\)) 之间建立分离。

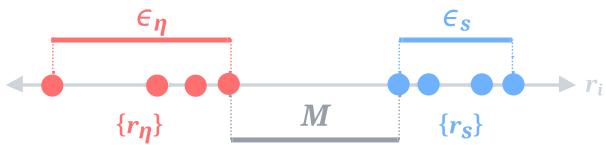
我们定义信号和噪声分数的“邻域” (分布范围) :

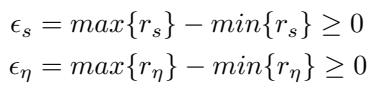
以及这些邻域之间的 边际 (\(M\)) 和 距离 (\(D\)):

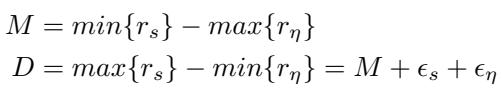
可视化有助于直观理解:

作者推导出了明确的误差界限。他们证明，随着边际 \(M\) 的增加，AdaPool 近似最佳权重的误差会缩小。

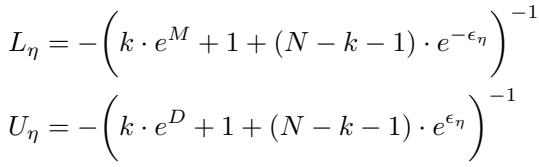
结论: 只要 Transformer 能够学习到一个嵌入空间，使得信号向量比噪声向量更类似于查询 (创造一个正的边际 \(M\)) ，AdaPool 就会以指数速度将噪声向量的权重推向零。

选择查询向量

为了让 AdaPool 工作，我们需要一个查询 \(\mathbf{x}_q\)。

• 坏主意: 使用固定的学习参数 (如 CLS token) 。这是静态的，无法适应旋转或移动的信号分布。
• 坏主意: 使用输入的平均值。这会被噪声破坏。
• 好主意: 从 信号子集 中选择一个向量。

在许多任务中，我们至少知道一个可能相关的向量。在 RL 中，这可能是智能体自身的状态向量。在视觉中，它可能是图像的中心补丁 (假设主体位于中心) 。这锚定了注意力机制，使其能够从噪声中“拉”出其他相关向量。

实验验证

理论预测标准池化会随着信噪比的波动而失效，而 AdaPool 应保持稳定。实验生动地证实了这一点。

1. 合成监督学习

研究人员创建了一个点集数据集，显式控制 \(N\) (总点数) 和 \(k\) (找到目标质心所需的信号点数) 。这允许在 0.01 到 1.0 的整个信噪比谱系中进行测试。

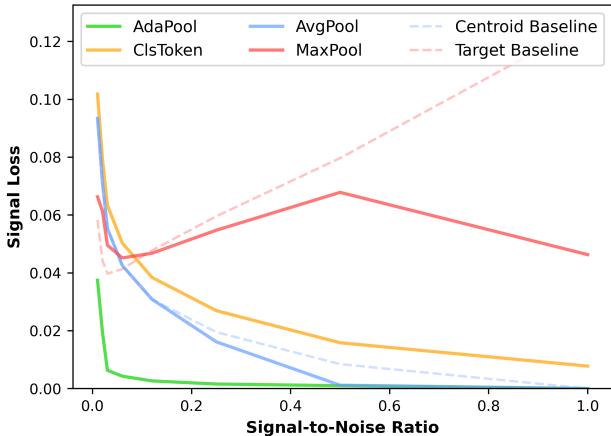
图 4 分析:

• AvgPool (蓝色): 在 SNR=1.0 (纯信号) 时表现良好，但随着噪声增加 (SNR 下降) ，误差飙升。
• MaxPool (红色): 在极低 SNR (大海捞针) 下表现尚可，但随着信号变得更复杂 (高 SNR) ，表现失效。
• AdaPool (绿色): 占据优势。它紧贴图表底部，在几乎整个谱系中保持接近零的信号损失。它成功地调整了策略。

2. 多智能体强化学习 (MPE)

在多粒子环境 (MPE) 中，智能体必须合作或竞争。研究人员引入了“噪声智能体”——存在但与任务无关的粒子。

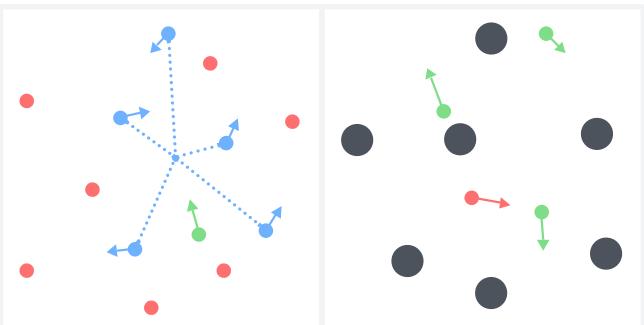
他们测试了“简单质心”任务 (前往信号智能体的中心) 和“捕食者-猎物”捉迷藏游戏。

结果 (简单质心) : 随着信号智能体数量减少 (降低 SNR) ，标准方法崩溃了。

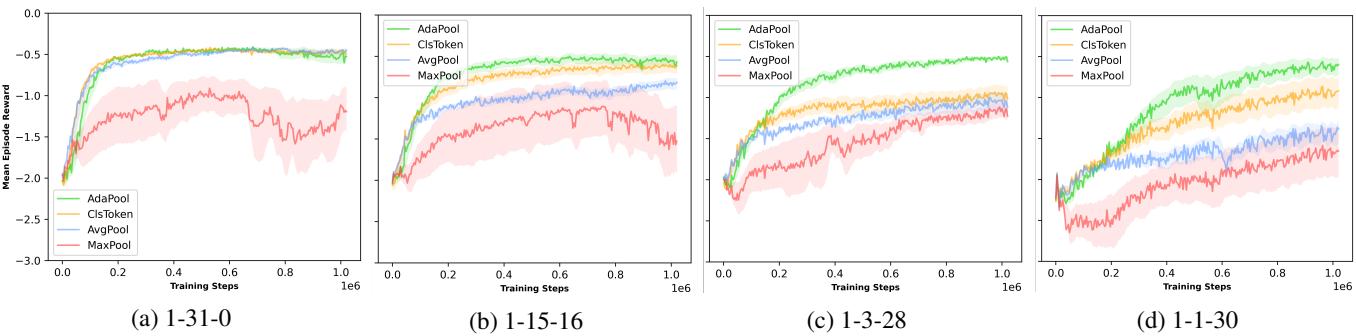
• 图 (c) 和 (d) 代表高噪声场景。看那条绿线 (AdaPool)。它收敛到了高奖励，而 AvgPool 和 MaxPool 则十分挣扎。MaxPool 在这里特别糟糕，因为任务需要聚合来自 多个 信号智能体的位置，这是 MaxPool 无法做到的。

结果 (简单捉迷藏) : 在捉迷藏场景中，他们增加了障碍物 (噪声) 的数量。

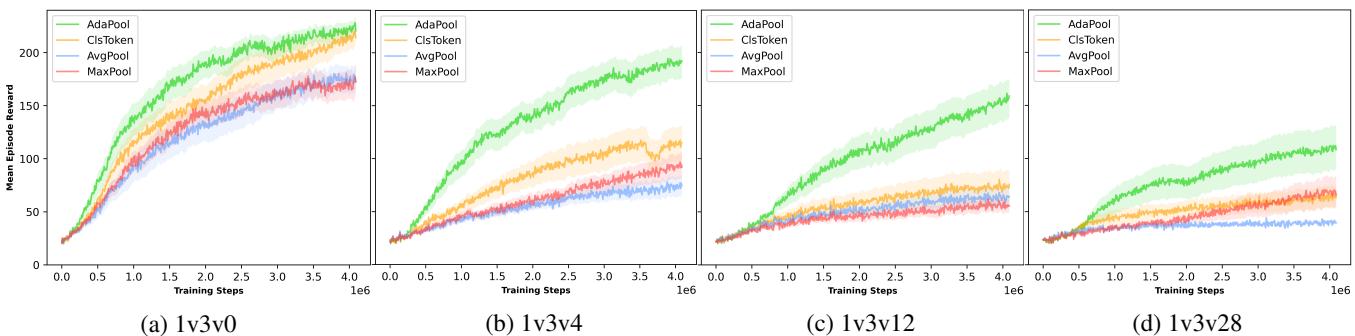
随着障碍物增加 (从左图移至右图) ，AvgPool (蓝色) 和 MaxPool (红色) 的性能急剧下降。AdaPool (绿色) 保持了最高的胜率，证明了其样本效率和对视觉混乱的鲁棒性。

3. 关系推理 (BoxWorld)

BoxWorld 是一个需要复杂关系推理的益智游戏 (钥匙打开锁，锁里包含其他钥匙) 。它视觉稀疏但逻辑密集。

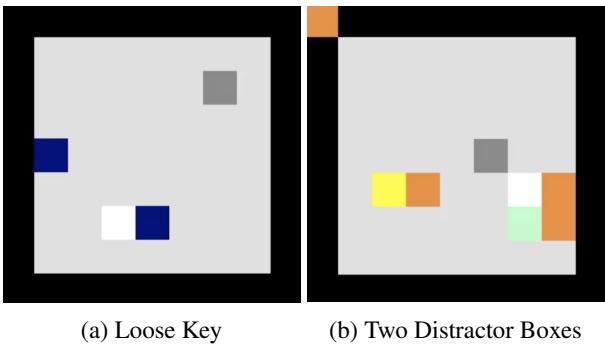
作者测试了两种观察类型:

1. 基于实体: 高信号，低噪声。
2. 基于像素: 大量噪声 (主要是空的黑色空间) 。

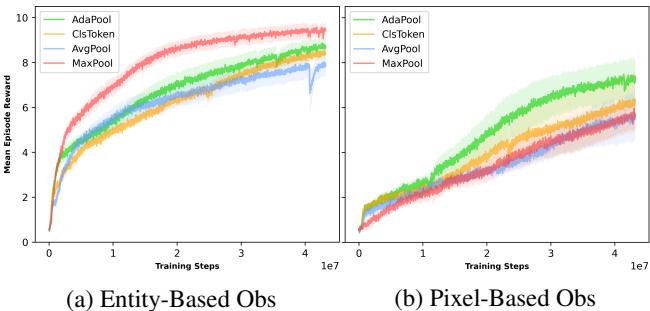
这个结果非常引人入胜。在 (a) 基于实体 中，MaxPool (红色) 实际上学习得很快。为什么？因为“宝石” (目标) 是白色的 (像素值 1.0) 。MaxPool 偏向于找到这个最大值。然而，在 (b) 基于像素 中，噪声压倒了 MaxPool 幼稚的偏置。AdaPool (绿色) 仍然是唯一能在高噪声像素机制下解决谜题的一致表现者。

4. 计算机视觉 (CIFAR)

这适用于真实图像吗？他们在 CIFAR-10 和 CIFAR-100 上训练了视觉 Transformer (ViT)。 挑战在于: 图像中 AdaPool 的“查询”是什么？ 他们假设图像的中心补丁通常包含感兴趣的物体。

他们比较了:

• Ada-Corner: 查询是角落补丁 (可能是背景/噪声) 。
• Ada-Focal: 查询是中心补丁 (可能是信号) 。
• Ada-Mean: 查询是所有补丁的平均值。

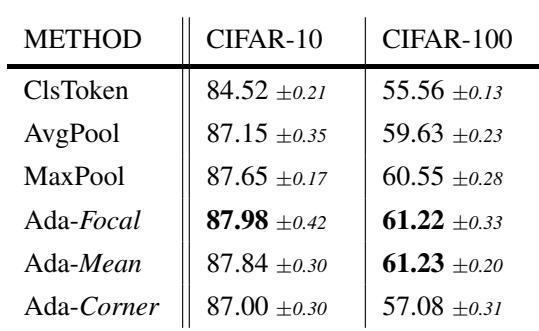
Ada-Focal 和 Ada-Mean 优于标准的 CLS token 和 AvgPool。即使是使用噪声查询的 Ada-Mean , 表现也出奇地好，这表明只要查询捕捉到了图像的大致“主旨”，注意力机制就足够鲁棒，可以过滤噪声。

结论

在 Transformer 中选择池化层通常是一个后知后觉的决定，但这项研究表明这是一个关键的架构决策。

• AvgPool 假设一个干净、平衡的世界。当噪声占主导地位时，它会失效。
• MaxPool 假设一个稀疏、简单的世界。当信号复杂时，它会失效。
• AdaPool 不做任何假设。通过利用注意力机制，它动态地对输入进行加权，有效地“学习如何池化”。

作者证明了 AdaPool 不仅仅是一个经验性的技巧；它近似于数学上的最佳矢量量化器。对于设计自主系统的学生和研究人员来说——无论是导航杂乱房间的机器人还是玩复杂游戏的智能体——用自适应注意力层替换最后的 mean() 可能是显著提高鲁棒性的最简单方法。