神经网络训练中隐藏的普适性与超坍缩之谜

如果你曾经训练过大型神经网络，你会知道这个过程感觉有点像炼金术。你混合数据集、架构和优化器，盯着损失曲线 (希望) 它下降。我们已经开发出了“缩放定律” (Scaling Laws) ——这是根据模型大小和计算预算预测模型最终性能的经验幂律。但模型达到目标的路径——即训练动力学——在很大程度上仍然是一个混乱且不可预测的黑盒。

直到现在。

在一篇引人入胜的新论文 Scaling Collapse Reveals Universal Dynamics in Compute-Optimally Trained Neural Networks 中，来自纽约大学和 Google DeepMind 的研究人员揭示了训练混乱中隐藏的对称性。他们证明，如果“计算最优地” (即有效地平衡模型大小和训练持续时间) 训练模型，微型模型和巨型模型的损失曲线实际上是相同的。

这种现象被称为 缩放坍缩 (Scaling Collapse) , 它表明尽管现代 AI 极其复杂，但学习过程存在一个简单、普适的“形状”。更令人惊讶的是，在特定条件下，这种普适性变得如此精确，以至于它打破了实验的标准噪声底 (noise floor) ——这一现象被称为 超坍缩 (Supercollapse) 。

在这篇文章中，我们将解构这种普适性背后的数学原理，探索预测它的简单模型，并讨论为什么这对深度学习缩放的未来至关重要。

追求计算最优

在理解坍缩之前，我们需要理解实验设置。研究人员专注于 计算最优 (compute-optimal) 训练。这个概念因 “Chinchilla” 论文 (Hoffmann et al., 2022) 而普及，它提出了一个简单的问题: 对于给定的 FLOPs (计算操作) 预算，模型参数 (\(p\)) 和训练 token (\(t\)) 的最佳分配是什么？

如果你有巨大的预算，你不应该只是把一个小模型训练一万亿年，也不应该只训练一个庞大的模型一个 epoch。在模型大小和数据集大小共同增长之间存在一个“甜蜜点”平衡。

研究人员训练了一个“缩放阶梯”——一系列宽度递增的 Transformer 和 MLP——其中每个模型都针对其特定的计算最优视界 \(t^*(p)\) 进行了训练。

发现: 普适损失曲线

当你绘制这些不同模型的原始损失曲线时，它们看起来截然不同。较大的模型以不同的损失开始，并收敛到更低的值。然而，作者发现这些曲线实际上是单一普适轨迹的影子。

为了看到这一点，他们对损失曲线进行了归一化处理。他们通过重新缩放时间和损失定义了 归一化损失曲线 \(\ell(x, p, \omega)\):

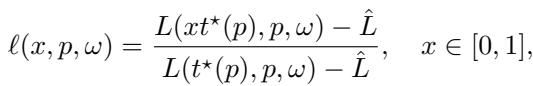
这里:

• \(x\) 是 归一化计算量 (范围从 0 到 1) ，代表已使用的训练预算比例。
• \(\hat{L}\) 是不可约损失 (可能的最低损失，例如数据中固有的熵) 。
• 分母相对于最终达到的损失对进度进行归一化。

当研究人员将这种变换应用于大小迥异的模型 (从 10M 到 80M 参数) 时，发生了惊人的事情。

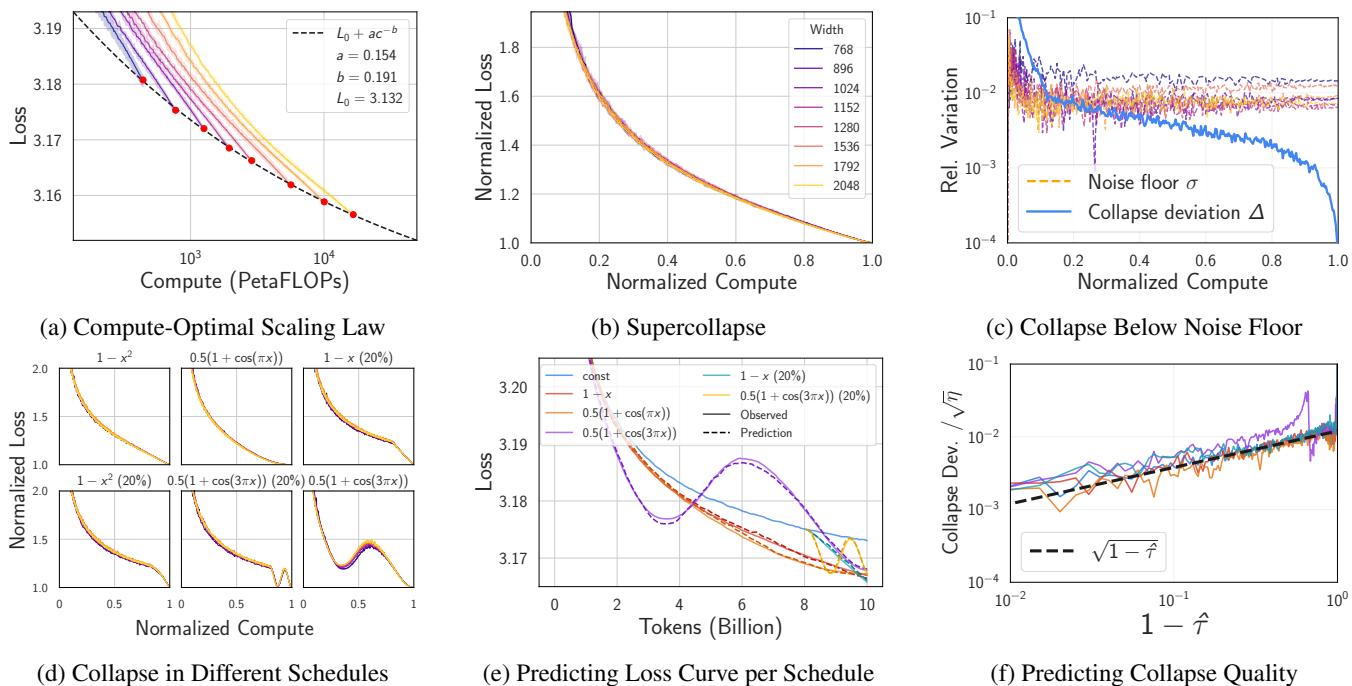
如上图 Figure 1(b) 所示，这些曲线相互坍缩重合了。一个处于 50% 训练预算的小模型，其行为在统计上与处于 其 50% 预算的大模型完全相同。这就是 缩放坍缩 。 这意味着相对进展的速率与规模无关。

不可约损失的作用

这种归一化的一个关键细节是减去 \(\hat{L}\)，即不可约损失。如果你尝试在不考虑数据集中固有噪声 (“熵底”) 的情况下进行归一化，坍缩就会失败。

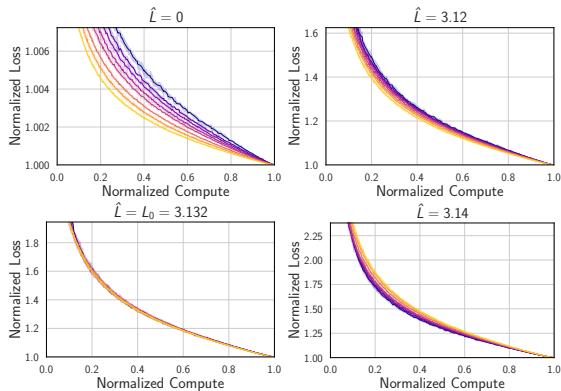
Figure 2 展示了这种敏感性。当 \(\hat{L}\) 与估计的不可约损失 \(L_0\) 匹配时，坍缩最为剧烈。这种敏感性实际上很有用——它可以作为一种合理性检查，用来验证我们是否正确估计了数据集的根本限制。

进入“超坍缩”

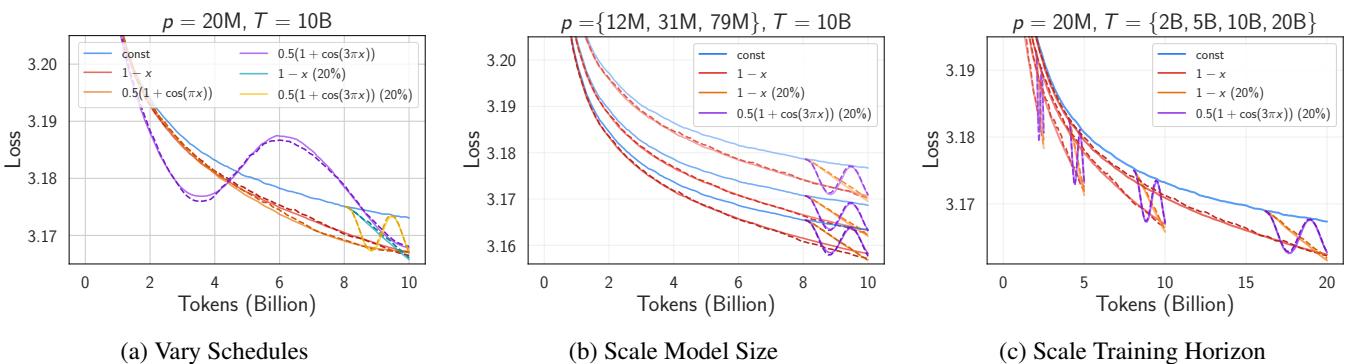
在恒定学习率下，这种坍缩已经足够有趣，但现代训练使用调度策略 (如线性衰减或余弦退火) 随着训练的进行降低学习率。当研究人员分析这些调度策略时，他们发现了一些奇怪的事情。

在学习率衰减的情况下，来自不同模型的归一化曲线彼此之间的匹配度，竟然比同一模型的两个随机种子之间的匹配度更好。

为了量化这一点，他们定义了 坍缩偏差 (Collapse Deviation) \(\Delta(x)\) (模型之间的差异) ，并将其与 噪声底 (Noise Floor) \(\sigma(x, p)\) (随机种子之间的差异) 进行了比较。

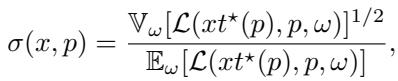
在标准实验中，你会预期不同模型大小之间的变化 (\(\Delta\)) 大于或至多等于随机噪声 (\(\sigma\))。

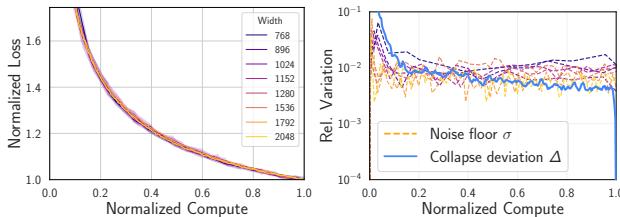
在恒定学习率下 (Figure 3) ，\(\Delta\) 大致等于 \(\sigma\)。但回看 Figure 1(c) 。 在衰减调度下，蓝线 (\(\Delta\)) 跌落到了橙线 (\(\sigma\)) 下方 。

这就是 超坍缩 (Supercollapse) 。 它意味着计算最优模型的归一化动力学极其刚性，受到一种普适定律的约束，该定律会随着学习率的下降而抑制方差。

解释这种现象

为什么会发生这种情况？作者提供了两部分的理论解释: 一部分基于幂律，另一部分基于随机梯度下降 (SGD) 的噪声动力学。

1. 幂律连接

从经验上看，神经缩放定律通常遵循幂律之和:

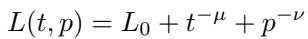
在这个方程中，\(t^{-\mu}\) 代表由于训练时间有限导致的误差，而 \(p^{-\nu}\) 代表由于模型大小有限导致的误差。

研究人员在数学上证明，如果你求解最佳计算预算，你会强制这两项之间达到平衡:

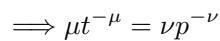
当你将这个平衡代回损失方程并对其进行归一化时，对 \(p\) (模型大小) 的依赖完全抵消了:

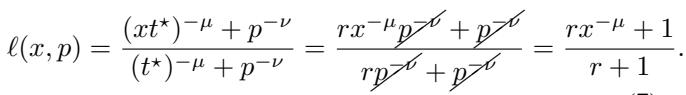
右边的结果只取决于 \(x\) (时间) 和常数——\(p\) 消失了。这解释了为什么曲线会坍缩: 计算最优性迫使有限宽度误差和有限时间误差同步缩放。

2. SGD 噪声的简单模型

幂律解释适用于恒定学习率，但它无法捕捉余弦或线性衰减调度下损失曲线的复杂形状。为了解释超坍缩，作者将训练建模为确定性路径加上 SGD 注入的噪声。

他们利用了学习动力学的线性化模型。令人惊讶的是，他们发现由特定学习率调度引起的损失变化可以通过一个简单的方程来预测:

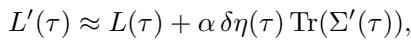
这里，损失 \(L'\) 是原始损失加上一项，该项取决于学习率的变化 \(\delta \eta\) 和 梯度协方差的迹 (\(\text{Tr}(\Sigma')\))。这个迹衡量了梯度中噪声的大小。

这个简单的模型惊人地有效。

如 Figure 6 所示，这个理论模型 (虚线) 准确预测了 Transformer 在 CIFAR-5M 上跨各种调度和模型大小的真实训练曲线 (实线) 。

3. 为什么会超坍缩？ (方差缩减)

理论模型也解释了为什么超坍缩会击穿噪声底。归根结底是相关性。

当我们归一化损失曲线时，我们将当前损失除以该特定运行的最终损失。由于 SGD 噪声在时间上是相关的，因此在训练中期“运气不好” (损失较高) 的运行，在结束时很可能也“运气不好”。通过除以最终损失，我们本质上是在使用训练结束时的状态作为一个 控制变量 (control variate) 。

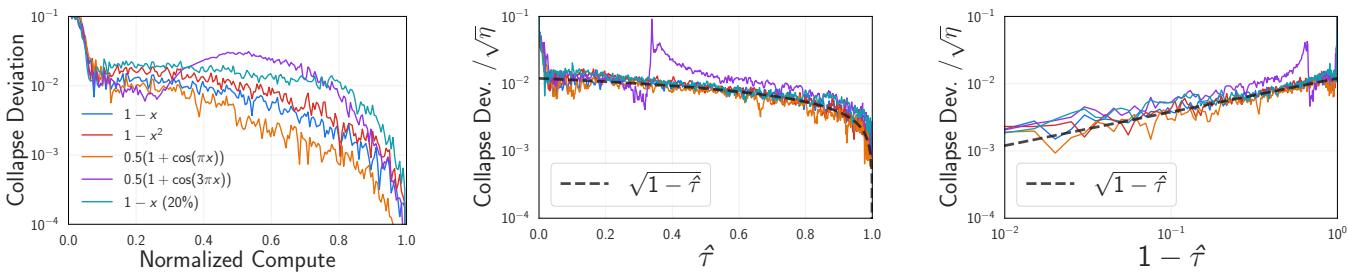
Figure 8 证实了这一点。坍缩曲线的方差随着学习率 \(\eta\) 的衰减而减小。这种缩放遵循 \(\sqrt{\eta(1-\hat{\tau})}\)。随着学习率降至零，相关的噪声几乎完美抵消，驱使坍缩偏差趋向于零。

实际应用: 一种诊断工具

除了理论上的美感，超坍缩对 AI 工程师来说也是一个强大的工具。因为坍缩是如此精确，它可以作为“糟糕”缩放的敏感检测器。

如果你缩放模型宽度，但未能正确缩放超参数 (如初始化或学习率) ，或者如果你的数据指数是错误的，坍缩就会被破坏。

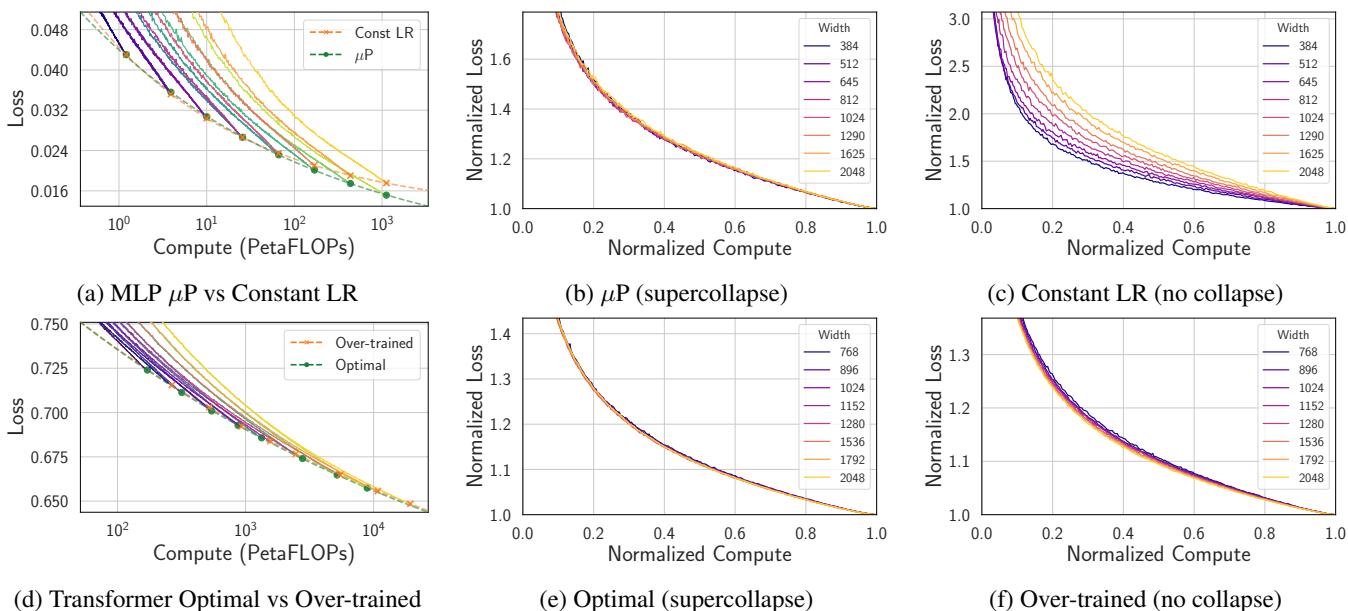
在 Figure 4 中，我们看到了两个失败的例子:

1. 上行: 跨模型使用恒定学习率 (而不是正确的 \(\mu P\) 参数化) 破坏了坍缩。
2. 下行: 使用次优的数据指数 (\(\gamma=1.2\) 而不是 \(1.02\)) 导致曲线分离。

这意味着你可以使用缩放坍缩来调整你的缩放定律。你不需要训练模型直到完成并拟合最终点 (这充满噪声) ，而是可以调整超参数，以最大化整个训练轨迹中坍缩的紧密度。

结论

论文 “Scaling Collapse Reveals Universal Dynamics” 为深度学习的底层物理学提供了一瞥。它表明，训练大型模型不仅仅是沿着损失景观的混乱下降，而是一个受普适动力学支配的、结构化的、可预测的过程。

给学生和从业者的关键结论:

1. 普适形状: 计算最优训练的模型在归一化后遵循单一、普适的学习曲线。
2. 超坍缩: 学习率衰减有效地抑制了方差，使得跨规模的归一化曲线比同规模的随机种子匹配得更好。
3. 诊断能力: 如果你的损失曲线没有坍缩，你的缩放策略 (超参数或数据混合) 很可能是次优的。

通过关注整个损失曲线的动力学而不仅仅是最终数字，我们对神经网络如何缩放有了更丰富的理解——为下一代基础模型更高效、更稳健的训练铺平了道路。