引言

深度学习中最深奥的谜团之一就是泛化现象。我们通常通过“插值”的视角来理解泛化: 如果神经网络看到足够多的训练样本 (图表上的点) ，它就能学会一条连接这些点的平滑曲线，从而能够预测位于训练样本之间的点的数值。

然而，在某些特定的设定下，神经网络表现出了一种无法用插值解释的行为。它们学会了外推 。 它们能够处理远超其训练数据边界的输入——有时甚至是无限的。当一个在短序列上训练的网络突然能够解决数千倍长度序列的任务时，这意味着网络不仅仅是拟合了一条曲线；它发现了一种底层的算法。

像梯度下降这样简单的过程——其目的仅仅是最小化特定训练数据上的误差——是如何偶然发现一个通用算法的？

这篇博客将深入探讨一项近期的研究，该研究利用流式奇偶校验任务 (Streaming Parity Task) 剖析了这一现象。通过分析循环神经网络 (RNN) 的学习动力学，我们将探索一个将神经表示建模为相互作用粒子的理论框架。我们将看到“隐式状态合并”是如何驱动网络从死记硬背走向算法上的完美。

问题: 从有限数据到无限泛化

为了研究算法学习，我们需要一个无法通过简单近似来解决的任务。这就是流式奇偶校验任务的用武之地。

这个任务很简单但具有非线性: 给定一串二进制数字流 (0 和 1) ，如果目前为止看到的 1 的总数是偶数，网络必须输出 0；如果是奇数，则输出 1。这相当于计算数据流的累积异或 (cumulative XOR) 。

关键的设置如下: 研究人员在有限长度 (例如，长度不超过 10) 的序列上训练 RNN。然后，他们在长度为 10,000 的序列上对其进行测试。

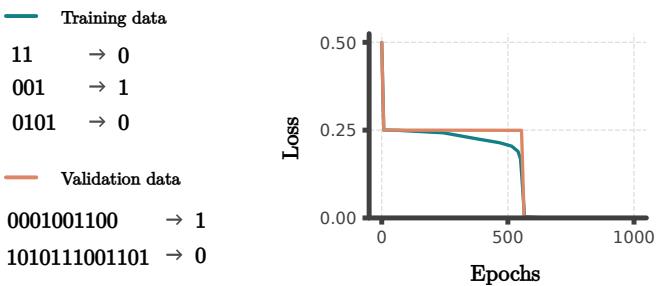
循环网络在简单任务上的序列长度泛化。左图: 流式奇偶校验任务的示例序列，包括训练数据集 (短序列) 和验证数据集 (长序列) 。右图: 循环神经网络在流式奇偶校验任务训练期间的均方误差。注意，即使对于比训练数据长得多的序列，损失也会降至零。测试序列长度达到了 10000。

如图 1 所示，网络在比训练集长几个数量级的序列上实现了接近零的损失。由于“长序列”域与“短序列”域完全不相交，插值是不可能的。网络必须已经学会了奇偶校验的精确逻辑。

背景: RNN 与自动机

要理解网络是如何学会这一点的，我们需要深入“黑盒”内部。解释 RNN 的一种标准方法涉及动力系统，但对于算法任务，一个更强大的视角是自动机理论 。

目标算法: DFA

流式奇偶校验任务可以由一个仅有两个状态的确定性有限自动机 (DFA) 完美描述。

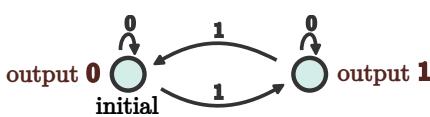
解决流式奇偶校验任务的双状态 DFA 示例。输入 1 会在状态之间切换，输入 0 则保持当前状态。

在这个 DFA (图 2) 中，系统实际上拥有 1 比特的记忆: “偶数” (输出 0) 或“奇数” (输出 1) 。

  • 如果它看到 0，它保持在当前状态。
  • 如果它看到 1，它转换到另一个状态。

从神经网络中提取自动机

RNN 在连续的向量空间中运行，而不是离散状态。其定义方程为:

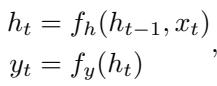
描述 RNN 隐藏状态更新和输出映射的方程。

这里，\(h_t\) 是高维隐藏状态向量。为了检查 RNN 是否学会了 DFA，我们将隐藏向量 \(h_t\) 视为“状态”。如果网络正在通过算法解决任务，那么无数种可能的隐藏向量应该聚类成一组有限的功能状态。

研究人员使用了一种技术来提取这些自动机。他们将序列输入网络并观察产生的隐藏向量。如果两个不同的序列导致的隐藏向量彼此非常接近 (欧几里得距离 \(<\epsilon\)) ，它们就被视为同一个“状态”。

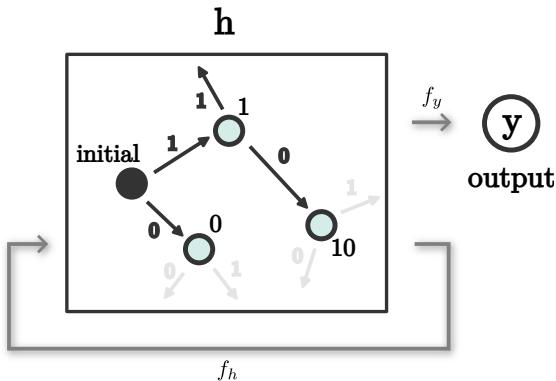
说明自动机提取过程的图表。隐藏向量被聚类以形成离散的状态和转换。

通过在训练过程中跟踪这些状态，我们可以实时观察算法的演变。

观察结果: 学习的各个阶段

当我们可视化训练过程中提取的自动机时，一个惊人的模式出现了。学习过程不是均匀的；它发生在不同的阶段。

训练期间从 RNN 隐藏层提取的自动机。第一阶段: 树拟合。第二阶段: 导致泛化的状态合并。

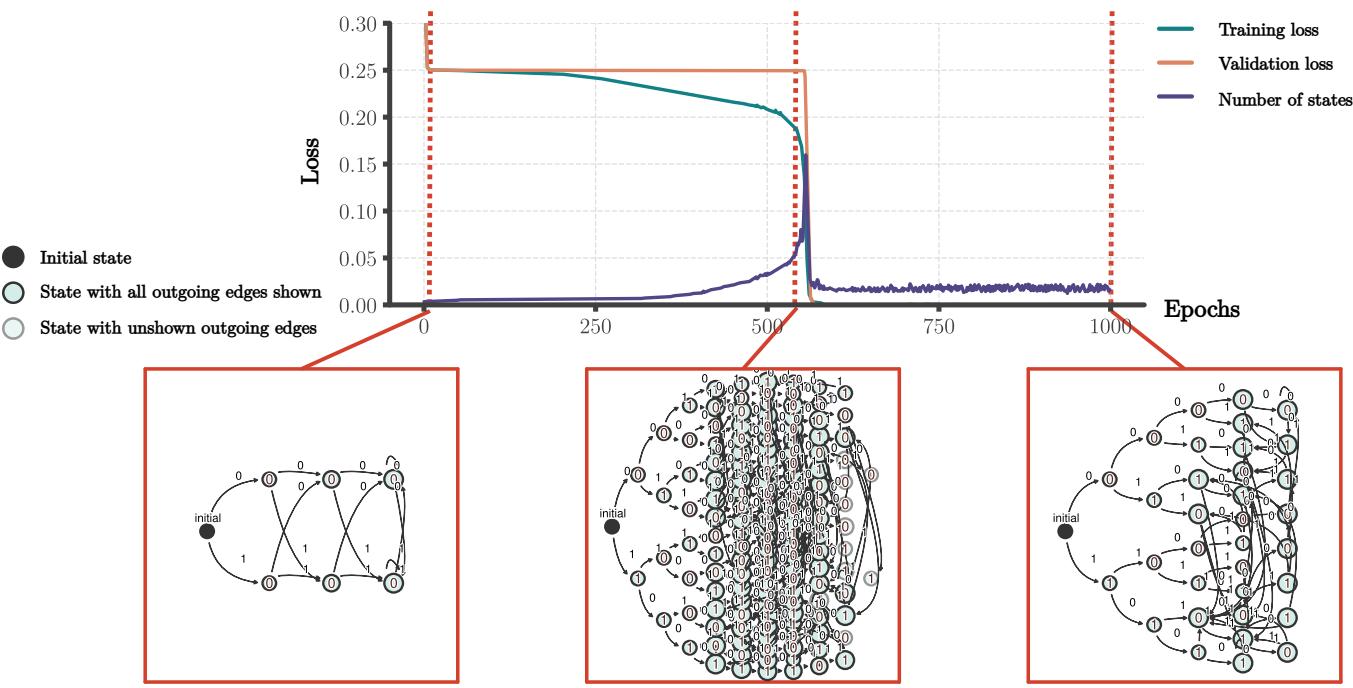
如图 4 所示，发展轨迹如下:

  1. 随机初始化: 自动机是混沌的，输出是随机的。
  2. 树拟合 (记忆) : 网络扩展其内部表示。它构建了一棵“树”，几乎每个唯一的序列都映射到一个唯一的隐藏状态。在这个阶段，网络正在记忆训练数据。它解决了短序列任务，但在长序列上失败了，因为它还没有学会循环结构。
  3. 状态合并 (泛化) : 这是关键时刻。树的不同分支开始坍缩。对应于不同序列的状态合并成单点。
  4. 有限自动机: 最终，自动机坍缩成一个有限循环 (类似于双状态 DFA) 。就在这一刻，无限序列上的验证损失降至零。

问题是: 为什么这些状态会合并? 梯度下降只关心最小化训练集上的误差。一个庞大的记忆树和紧凑的 DFA 一样能最小化训练误差。是什么力量驱动网络走向紧凑的、具有泛化能力的解？

核心方法: 隐式状态合并理论

作者提出了一个基于表示之间局部相互作用的理论框架。他们将隐藏状态建模为在高维空间中受梯度下降影响而移动的粒子。

直觉: 连续性

驱动力是网络映射函数的连续性 。 在神经网络中，将隐藏状态映射到输出的函数 (\(f_y\)) 是连续的。这意味着如果两个隐藏状态 \(h_1\) 和 \(h_2\) 彼此接近，它们的预测输出 \(y_1\) 和 \(y_2\) 也必须接近。

在训练过程中，网络更新其参数以最小化预测输出与目标输出之间的误差。如果两个隐藏状态比较接近，更新网络的梯度会根据它们共享的输出需求有效地“拉动”这些表示。

相互作用模型

为了形式化这一点，作者对对应于两个不同输入序列的两个隐藏表示 \(h_1\) 和 \(h_2\) 之间的相互作用进行了建模。

他们假设网络具有“表现力”，这意味着它有足够的参数来自由地近似平滑映射。他们不分析特定 RNN 架构的复杂权重更新，而是将隐藏状态和输出映射视为可优化的变量。

相互作用模型的示意图。网络被抽象为可优化的向量 h1, h2 和平滑输出映射 y。

  • (注: 该示意图将表示 \(h_1\) 和 \(h_2\) 概念化为可调整的点，它们通过优化以满足未来的输出需求 \(y_1 \dots y_N\)。) *

我们观察这两个表示中点周围输出映射的“局部线性近似”。序列的输出可以近似为:

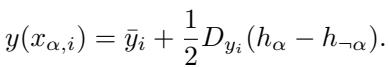
显示围绕表示均值的输出映射线性近似的方程。

这里，\(D_{y_i}\) 代表输出函数的梯度 (斜率) 。目标是最小化均方误差 (MSE) 损失:

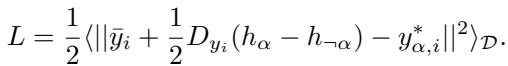
线性近似模型中的均方误差方程。

吸引动力学

通过对隐藏状态和输出映射求导来计算该损失的梯度，研究人员推导出了一个微分方程组，描述了 \(h_1\) 和 \(h_2\) 之间的距离 (\(||dh||^2\)) 随时间的变化。

虽然完整的推导很复杂，但由此产生的表示距离动力学可以提炼为一个自包含的系统。控制这些“粒子”速度的关键方程是:

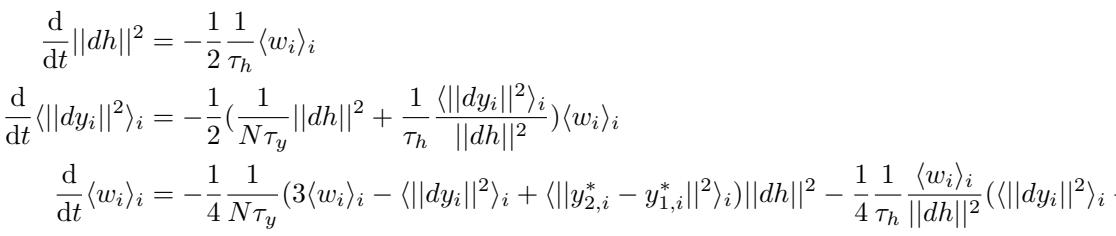
描述表示距离和输出对齐演变的微分方程组。

变量 \(w_i\) 本质上衡量了输出梯度与目标差异之间的对齐程度。从这些动力学中得出的关键结论是不动点分析 。 我们想知道这些动力系统会在哪里稳定下来。距离 \(||dh||^2\) 是会趋向于零 (合并) 还是保持正值 (分离) ？

求解最终的表示距离得出:

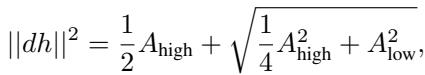
包含 A_high 和 A_low 项的最终表示距离方程。

这个解取决于两个关键项，\(A_{high}\) 和 \(A_{low}\)。最重要的是 \(A_{low}\)，它代表目标输出的差异:

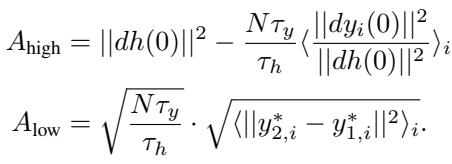
A_low 的定义，显示它取决于目标输出 y<em>2 和 y</em>1 之间的差异。

合并条件

数学推导揭示了两个状态合并的严苛条件。为了使距离 \(||dh||^2\) 变为零 (合并) ，我们特别需要 \(A_{low} = 0\)。

观察 \(A_{low}\) 的定义，这意味着:

\[ \forall_i \quad y_{2,i}^* = y_{1,i}^* \]

翻译过来就是: 当且仅当两个隐藏状态对于训练集中所有可能的未来序列都具有完全相同的目标输出时，它们才会合并为一个。

如果哪怕有一个未来序列导致状态 \(h_1\) 需要与状态 \(h_2\) 不同的输出，网络就必须将它们分开以满足训练损失。但是，如果它们在未来的功能上是完全相同的，梯度下降的隐式偏差 (通过连续性) 就会产生一种吸引力，将它们坍缩在一起。

此外，对初始条件的分析表明，合并取决于初始化的尺度。如果权重初始化得很小 (尺度 \(G < 1\)) ，那么对于“共享未来”很长的序列，吸引力会更强。

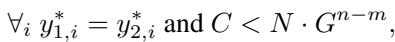
显示基于初始权重尺度 G 以及序列长度 n 和 m 的合并条件的方程。

这就解释了为什么网络不会仅仅停留在“树”阶段。树阶段将序列分开了。但是，由于树的许多分支实际上预测相同的未来 (例如，在奇偶校验中，任何两个具有偶数个 1 的序列在功能上是等价的) ，网络感受到一种持续的压力要将它们合并。

实验与结果

在流式奇偶校验任务上训练标准 RNN (ReLU 激活) 的实验结果与理论预测完美吻合。

1. “顿悟” (Grokking) 时刻

在初始训练阶段 (树拟合) ，长序列上的验证损失保持很高。然后，令人惊讶的是，它几乎瞬间降到了零。

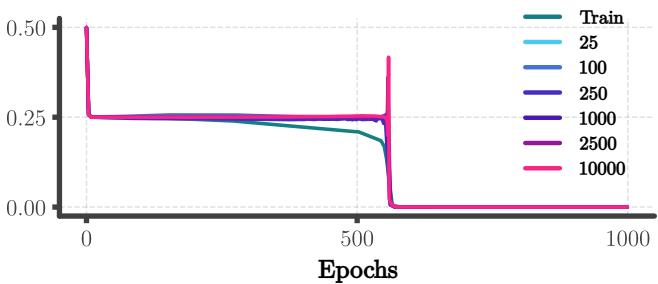
不同长度序列的验证损失。所有长度的损失同时突然下降。

图 6 展示了这种相变。损失对于所有长度同时下降的事实证实了网络已经从依赖长度的表示 (记忆) 切换到了独立于长度的表示 (算法) 。

2. 谁合并了？

理论预测只有对未来输出完全一致的状态对才会合并。数据证实了这一点。在分析的超过 100,000 对合并中, 100% 的对在所有未来输出上都一致。

此外，理论预测合并依赖于序列长度。存在一个阈值，在这个阈值之上，“吸引力”会克服初始的分离。

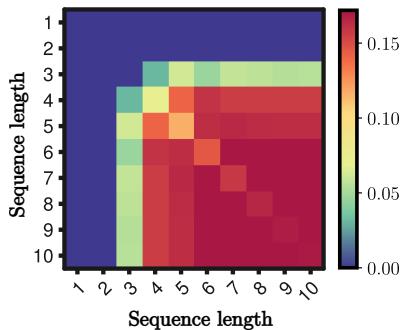
显示基于序列长度的同意对合并比例的热图。一旦最小序列长度达到阈值，合并就会发生。

图 7 说明短序列 (左上角) 很少合并，而长序列 (右下角) 频繁合并。这验证了理论发现，即合并力随匹配未来的长度而缩放。

3. 两阶段动力学: 先发散后合并

为什么网络首先拟合一棵树？为什么不立即合并？

研究人员将他们的相互作用模型扩展为“固定展开点”模型。这个更复杂的模型揭示了，如果两个表示具有不同的有效学习率 (当序列长度不同时会发生这种情况) ，它们最初会发散 (分开移动) ，然后吸引力才会将它们拉回到一起。

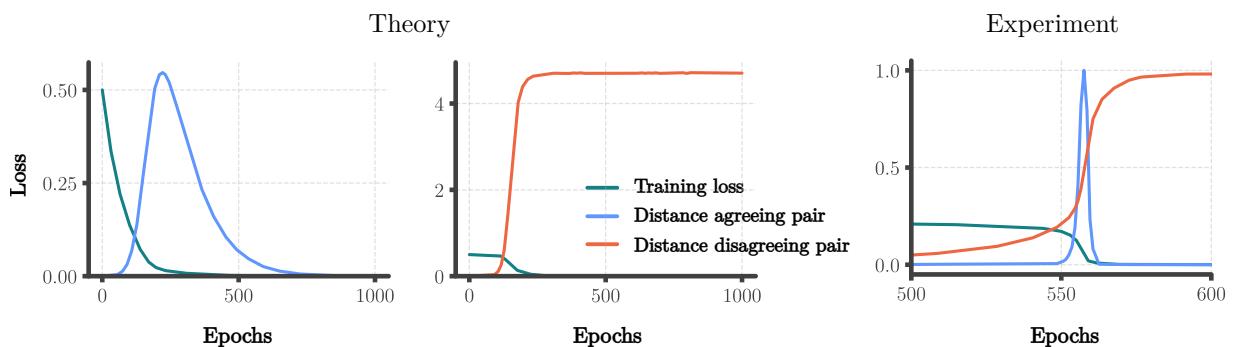
粒子动力学的理论与实验比较。同意对 (蓝色) 先发散，然后合并。不同意对 (橙色/红色) 发散并保持分离。

图 10 是该理论的“铁证”。

  • 理论 (左) : 蓝线 (同意对) 上升 (发散) ，然后跌至零 (合并) 。橙线 (不同意对) 上升并保持高位。
  • 实验 (右) : RNN 表现出完全相同的行为。

这种初始的发散创造了“树”阶段。最终的坍缩创造了“算法”阶段。

4. 冗余以及“丰富”与“懒惰”学习

网络学到的最终自动机并不总是最小的 2 状态机器。它通常包含冗余状态——即多个做同样事情但未能合并的状态。

然而，如果我们在这个学习到的网络上运行标准的约简算法 (Hopcroft 算法) ，它会完美地坍缩成任务解。

约简后的学习自动机。它与 2 状态奇偶校验解完美匹配。

研究还发现了一个基于数据量和权重初始化尺度的相变。

  • 懒惰机制 (Lazy Regime): 初始权重较大或数据较少。网络停留在树阶段 (记忆) 。
  • 丰富机制 (Rich Regime): 初始权重较小且数据充足。网络进入合并阶段 (算法学习) 。

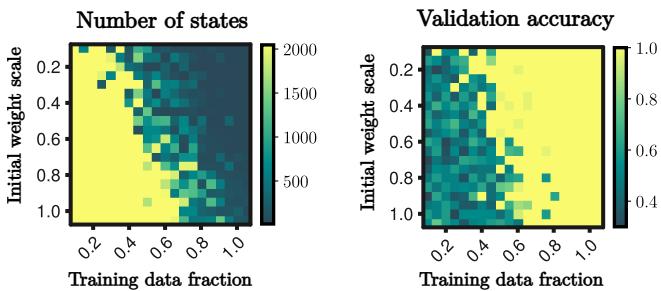
基于权重尺度和数据大小显示状态数量和验证准确率相变的热图。

图 9 显示了这两种机制之间的清晰边界。要获得无限泛化，你需要处于“丰富”机制 (热图的右下角) 。

Transformer 与 RNN

这篇论文简要涉及了 Transformer。它们是否表现出同样的“状态合并”动力学？

Transformer 有所不同，因为它们没有以同样方式顺序处理历史的循环隐藏状态。作者发现 Transformer 在其隐藏表示中没有显示出清晰的状态合并。然而，他们在注意力矩阵中观察到了类似合并的模式。

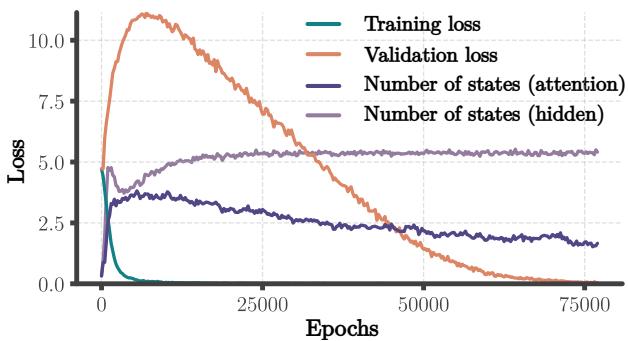
Transformer 的训练损失和状态计数。合并出现在注意力矩阵中，而不是隐藏层中。

这表明，虽然算法发展 (合并等效功能单元) 的机制可能是通用的，但这种合并发生的位置取决于架构。

结论与启示

这项研究提供了一个具体的数学解释，说明神经网络如何能够超越其训练数据来学习真正的算法。

关键要点:

  1. 通过外推进行泛化: 神经网络可以从有限数据中学习无限算法，而不仅仅是插值。
  2. 隐式偏差: 其机制是梯度下降的隐式偏差与连续性相结合，将“功能等效”的表示拉到一起。
  3. 相变: 学习发生在两个截然不同的阶段: 记忆数据 (树) 随后是压缩逻辑 (状态合并) 。
  4. 表示动力学: 我们可以将这些复杂的网络建模为相互作用的粒子系统，以预测它们何时以及如何学习。

这项工作弥合了深度学习的黑盒性质与计算机科学的结构化逻辑之间的鸿沟。对于神经科学来说，它表明“冗余”的神经表示可能是学习动力学的自然产物。对于 AI 安全，它强调了确保模型学习稳健算法而非脆弱启发式规则所需的特定条件 (初始化、数据量) 。

通过理解这些动力学，我们在设计不仅仅是记忆、而是真正理解支配其数据规则的网络方面迈进了一步。