引言: 生物学中制图师的困境

想象一下，你正试图在地球仪上导航，但你手头只有一张平面的纸质地图。你用尺子在地图上画了一条从纽约到伦敦的直线。在地图上，这看起来是最短的路径。但如果你要在现实中沿着这条路线飞行，你会发现，由于地球是弯曲的，你在地图上的“直线”实际上是地球仪上一条较长且效率低下的曲线。球面上的最短路径 (测地线) 在平面地图上看起来是弯曲的。

这种几何上的不匹配，正是研究人员在使用深度学习分析单细胞 RNA 测序 (scRNA-seq) 数据时面临的确切问题。

在计算生物学中，我们使用变分自编码器 (VAEs) 将成千上万个基因的巨大复杂性压缩到一个低维的“潜在空间”中——这是一个细胞特性的简化图谱。我们喜欢这个潜在空间，因为它允许我们执行线性插值 。 我们选取一个干细胞 (A点) 和一个成熟细胞 (B点) ，在潜在空间中画一条连接两者的直线，并假设这条线上的点代表了细胞成熟过程中所经历的生物学步骤。

但问题在于: 标准 VAE 无法保证潜在空间是平坦的。

就像墨卡托投影会扭曲大陆的大小一样，标准 VAE 也会扭曲生物学距离。潜在空间中的一条直线可能对应于实际基因表达空间中一条狂野的、生物学上不可能的轨迹。

这就是 FlatVI 登场的地方，这是一个由 Palma, Rybakov 等人提出的新框架，它强制 VAE 学习一个实际上是平坦 (欧几里得) 的潜在空间。通过在训练期间强制执行几何约束，FlatVI 确保了潜在图谱中的直线对应于复杂的细胞生物学世界中有意义的测地线路径。

在这篇文章中，我们将拆解 FlatVI 的数学原理，探索它如何利用黎曼几何和费雪信息度量 (Fisher Information Metric)，并了解为什么“拉平”曲线对于理解细胞发育至关重要。

背景: 数据的形状

为了理解 FlatVI，我们首先需要了解一些基本工具: VAE、黎曼几何以及单细胞数据的特性。

单细胞 RNA 测序与 VAE

单细胞 RNA 测序为我们提供了单个细胞内数千个基因活动的快照。由于这些数据是高维的 (每个细胞通常有 20,000+ 个维度) 且充满噪声，我们使用 VAE 来学习压缩表示。

VAE 由两部分组成:

  1. 编码器 (The Encoder): 将高维基因计数 (\(x\)) 压缩为低维潜在向量 (\(z\))。
  2. 解码器 (The Decoder): 从潜在向量重建原始数据。

在数学上，解码器定义了一个似然模型。对于单细胞数据，我们不仅仅输出数字；我们输出的是概率分布的参数。

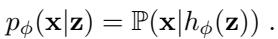
图1: VAE 的似然模型。

这里，\(h_{\phi}(z)\) 是解码器神经网络。它将潜在点 \(z\) 映射到生成数据 \(x\) 的分布参数。

几何上的脱节

核心问题在于我们要如何测量距离。在潜在空间 \(\mathcal{Z}\) 中，我们通常假设几何是欧几里得的。这意味着两点之间的距离就是标准的直线距离 (就像用尺子量一样) 。

然而，数据通常位于嵌入在高维空间中的弯曲“流形” (一种形状) 上。解码器 \(h\) 将我们简单的潜在空间映射到这个复杂的流形上。

如果我们不限制解码器，它可以随意扭曲和拉伸潜在空间。潜在空间某一部分的一小步可能会导致基因表达的巨大跳跃，而另一部分的一大步可能几乎不会改变细胞的状态。这种变化的“变化速度”意味着潜在空间具有非欧几里得几何结构 。

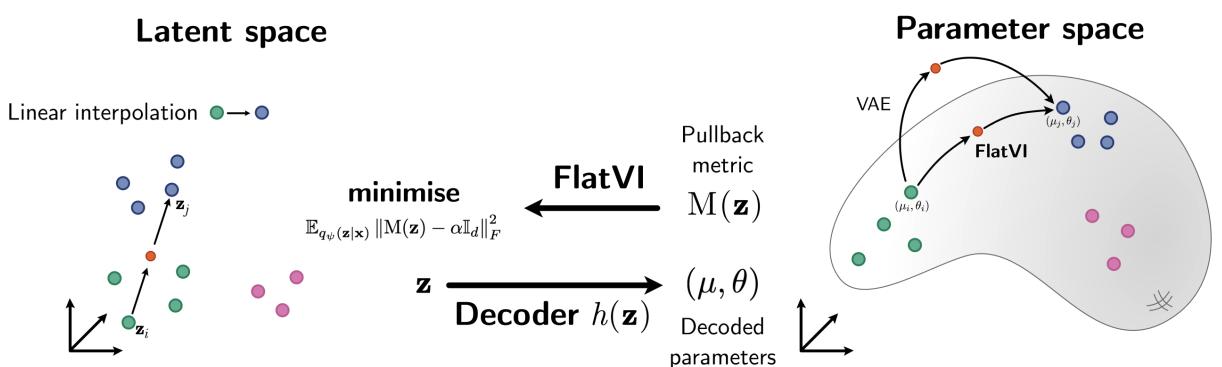
图 1: FlatVI 的概念可视化。左侧显示潜在空间，右侧显示复杂的参数流形。FlatVI 将左侧的线性路径与右侧的测地线路径对齐。

如图 1 所示，标准 VAE (上方路径) 允许潜在空间中的直线映射为偏离流形上最优路径的曲线。FlatVI (下方路径) 强制潜在直线直接映射到流形上的最短路径 (测地线) 。

核心方法: 强制平坦性

我们如何强制神经网络遵守欧几里得几何？我们必须测量曲率并在训练期间对其进行惩罚。这涉及到一个称为回拉度量 (Pullback Metric) 的概念。

回拉度量

想象一下你在地形 (流形) 上行走。你口袋里有一张地图 (潜在空间) 。 度量张量 (Metric tensor) \(M(z)\) 告诉你如何将地图上的一步转化为地形上的实际物理距离。

如果地图完全准确 (平坦且无失真) ，度量张量就是单位矩阵 (\(I\))。地图上的每一步都等于现实中恒定的一步。如果地图失真了，\(M(z)\) 会根据你所在的位置而变化。

在 VAE 中，我们可以通过观察解码器的变化来计算这个度量。具体来说，我们使用雅可比矩阵 \(\mathbb{J}_h(z)\)，它测量输出相对于输入的敏感度。

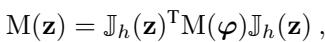
公式 7: 回拉度量的定义。

这个公式表明，潜在空间中的度量 \(M(z)\) 是数据空间的度量 \(M(\phi)\) 通过解码器“回拉”得到的。

统计流形与费雪信息

这里变得有趣起来了。由于 VAE 输出的是概率分布，因此“数据空间”不仅仅是一个物理表面；它是一个统计流形 。 这个流形上的点是概率分布。

测量分布之间距离的自然方法是费雪信息度量 (Fisher Information Metric, FIM) 。

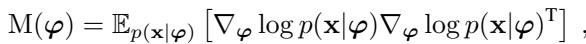
公式 6: 费雪信息度量 (FIM)。

FIM 衡量两个概率分布的可区分程度。如果轻微改变参数使分布看起来非常不同，则 FIM 很高 (距离大) 。如果分布看起来基本相同，则 FIM 很低。

通过将 FIM 代入我们的回拉方程，我们得到了一个度量 \(M(z)\)，它告诉我们当我们穿过潜在空间时，数据的概率分布变化得有多快。

平坦化损失

FlatVI 的目标很简单: 我们要让潜在空间度量 \(M(z)\) 在任何地方看起来都像一个缩放的单位矩阵。如果 \(M(z) \approx \alpha \mathbb{I}\)，这意味着曲率为零——空间是平坦的。

作者提出了一个正则化项，即平坦化损失 (Flattening Loss) :

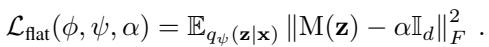
公式 8: 平坦化损失函数。

该损失函数计算实际计算出的度量 \(M(z)\) 与目标平坦度量 \(\alpha \mathbb{I}_d\) 之间的差异 (弗罗贝尼乌斯范数) 。

我们将此项添加到标准 VAE 损失函数 (ELBO) 中。这创造了一种权衡: 模型必须准确地重建数据 (ELBO)，同时保持潜在空间平坦 (平坦化损失)。

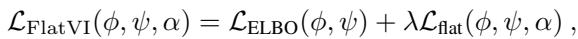
公式 9: 完整的 FlatVI 目标函数。

\(\lambda\) 是一个超参数，控制我们强制执行平坦度的严格程度。

为单细胞量身定制: 负二项分布案例

这篇论文的主要贡献之一是推导了负二项分布 (Negative Binomial, NB) 的特定度量，这是 scRNA-seq 计数数据的标准噪声模型。

以前大多数几何自编码器假设数据是高斯分布 (连续的) ，这并不适合离散的基因计数。作者明确地对生物数据的稀疏性和过度离散进行了建模。

负二项分布定义为:

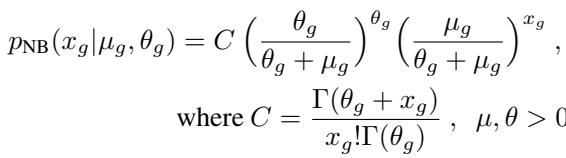
公式 10: 负二项分布概率质量函数。

这里，\(\mu_g\) 是基因的平均表达量，\(\theta_g\) 是逆离散度 (计数的分布范围) 。

作者针对这种特定的似然函数推导了精确的回拉度量。这使得 FlatVI 在数学上专门适用于测序数据:

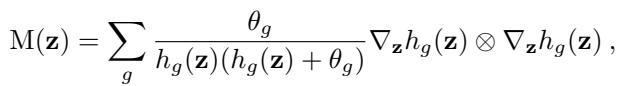
公式 11: 负二项分布 VAE 的显式回拉度量。

这个公式看起来可能很吓人，但它是该方法的核心驱动。它确切地告诉网络如何调整权重，以确保潜在变量 \(z\) 的变化会导致负二项输出分布发生一致的、“平坦的”变化。

实验与结果

强制这种几何结构真的有效吗？作者在模拟数据和真实世界的生物数据集上对 FlatVI 进行了测试。

模拟: 验证几何结构

首先，他们创建了一个已知基准真值几何结构的合成数据集。他们比较了标准负二项分布 VAE (NB-VAE) 与具有增加正则化强度 (\(\lambda\)) 的 FlatVI。

他们测量了潜在空间的两个关键属性:

  1. 黎曼度量的方差 (VoR): 理想情况下为 0。衡量当你四处移动时“尺子”尺寸变化的程度。
  2. 条件数 (CN): 理想情况下为 1。衡量空间在不同方向上被拉伸的程度。

图 2 可视化了这些指标。

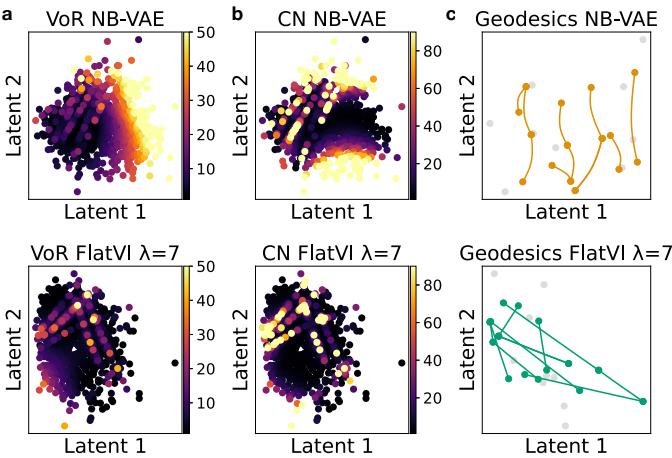
图 2: 潜在几何对比。上行: 标准 NB-VAE。下行: FlatVI。注意 FlatVI 如何降低黎曼度量的方差 (VoR) 和条件数 (CN)，创造一个更均匀的空间。图 (c) 显示 FlatVI 中的测地线 (最短路径) 变得更直。

在标准 VAE (上行) 中，你会看到度量高度失真的“热点” (黄色/红色) 。在 FlatVI (下行) 中，空间更冷 (紫色/蓝色) ，表明几何结构均匀且平坦。

此外，图 2(c) 显示了测地线路径。在标准 VAE 中，两点之间的最短路径是一条曲线。在 FlatVI 中，最短路径是一条直线——这正是我们进行线性插值所需要的。

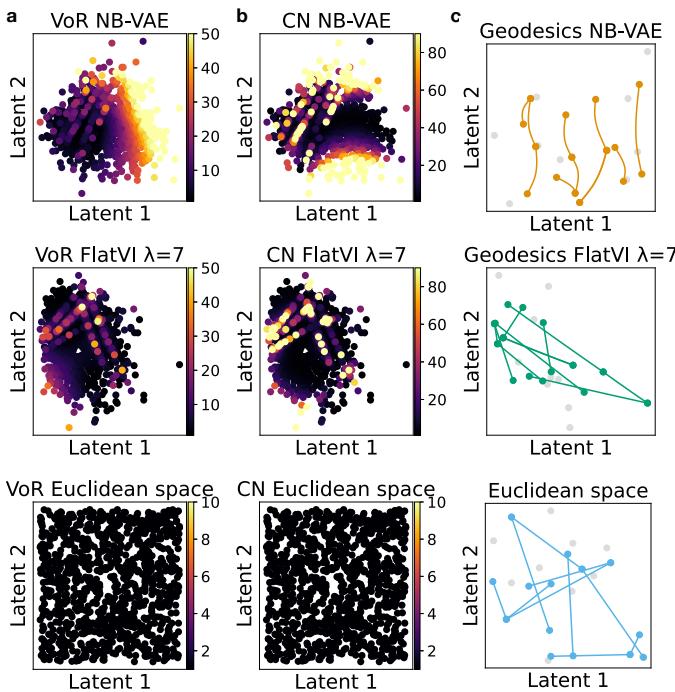
作为对比，下方的图 7 展示了一个完美的欧几里得空间是什么样子的 (下行) 。FlatVI (中行) 比标准 VAE (上行) 更好地近似了这种理想结构。

图 7: 与真实欧几里得空间的对比。下行显示理想情况 (完全平坦) 。FlatVI (中) 比未正则化的模型 (上) 更好地近似了这种结构。

轨迹推断: 预测细胞发育

真正的考验是生物数据。细胞随时间分化 (例如，从干细胞到心脏细胞) 。这是一个连续的过程。

作者使用最优传输 (OT) 来模拟这些轨迹。OT 是一个有效地将质量从一个分布移动到另一个分布的数学框架。具体来说，他们使用了条件流匹配 (OT-CFM) , 这是一种假设时间点之间存在直线路径的方法。

由于 OT-CFM 假设直线，如果底层表示支持直线，它的效果最好。

图 12 显示了在拟胚体 (EB) 数据集上的结果。目标是预测在训练期间被保留的中间时间点的细胞状态。

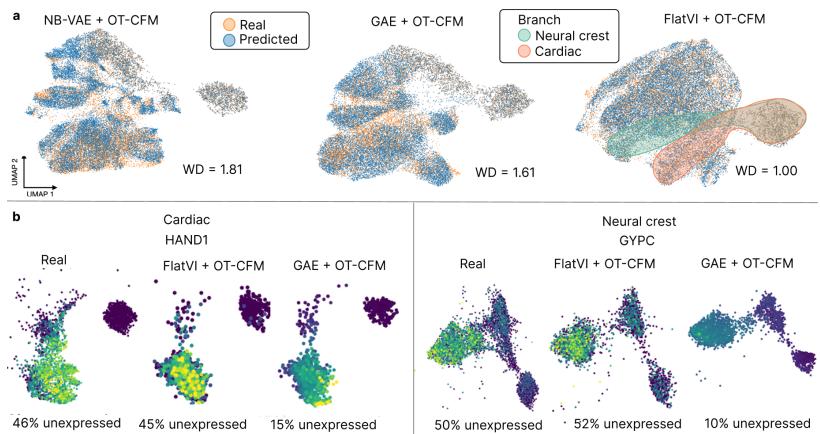
图 12: 预测 scRNA-seq 时间点。图 (a) 显示真实细胞 (橙色) 与预测细胞 (蓝色) 之间的重叠。FlatVI (右) 具有最佳重叠 (最低的 Wasserstein 距离) 。图 (b) 显示了基因表达的一致性。

与基准模型 (GAE 和 NB-VAE) 相比，FlatVI (图 12a 右侧面板) 在预测细胞和真实细胞之间实现了更紧密的重叠。这证明了 FlatVI 创建的“平坦”图谱是生物过程更准确的表示。

生物学一致性: 向量场

验证模型的另一种方法是查看 RNA 速率和向量场。我们可以推断细胞在潜在空间中的移动方向。如果潜在空间结构良好，这些向量应该从干细胞平滑地流向终末细胞类型。

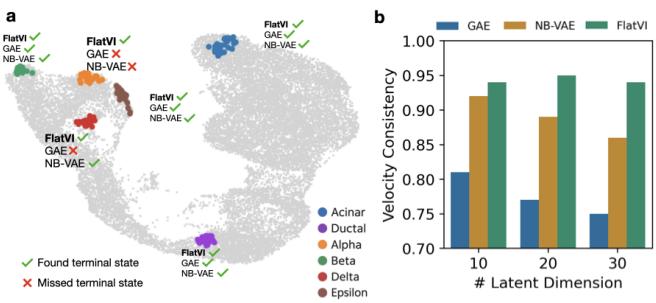
图 11 比较了胰腺数据上的向量场。

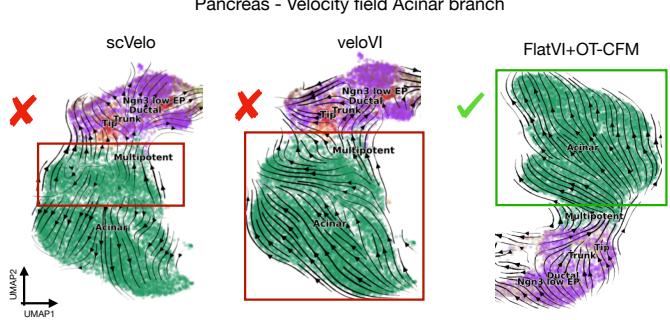
图 11: 向量场对比。标准速率方法 (scVelo, veloVI) 在腺泡分支 (Acinar branch) 上表现挣扎 (红叉) 。FlatVI 结合 OT-CFM 正确地模拟了流动 (绿色对勾) 。

FlatVI 成功捕捉了分支谱系。更令人印象深刻的是，当使用 CellRank (一种寻找终末状态的工具) 时，FlatVI 识别出了数据集中所有 6 种已知的终末细胞类型。NB-VAE 和 GAE 等标准方法遗漏了其中一些。

图 3: 终末状态识别。图 (a) 显示 FlatVI 正确识别了所有 6 种终末状态 (对勾) ，而基准模型遗漏了几个 (叉号) 。图 (b) 显示 FlatVI 具有更高的速度一致性。

线性插值: 终极测试

最后，作者回到了最初的动机: 流形插值 。 我们可以简单地在两个细胞之间画一条直线并生成一部生物学上逼真的发育电影吗？

他们将 FlatVI 与 GAGA (一种几何感知生成自编码器) 进行了比较。他们选取了一个多能细胞和一个成熟细胞，在潜在空间中进行线性插值，并解码路径上的基因表达。

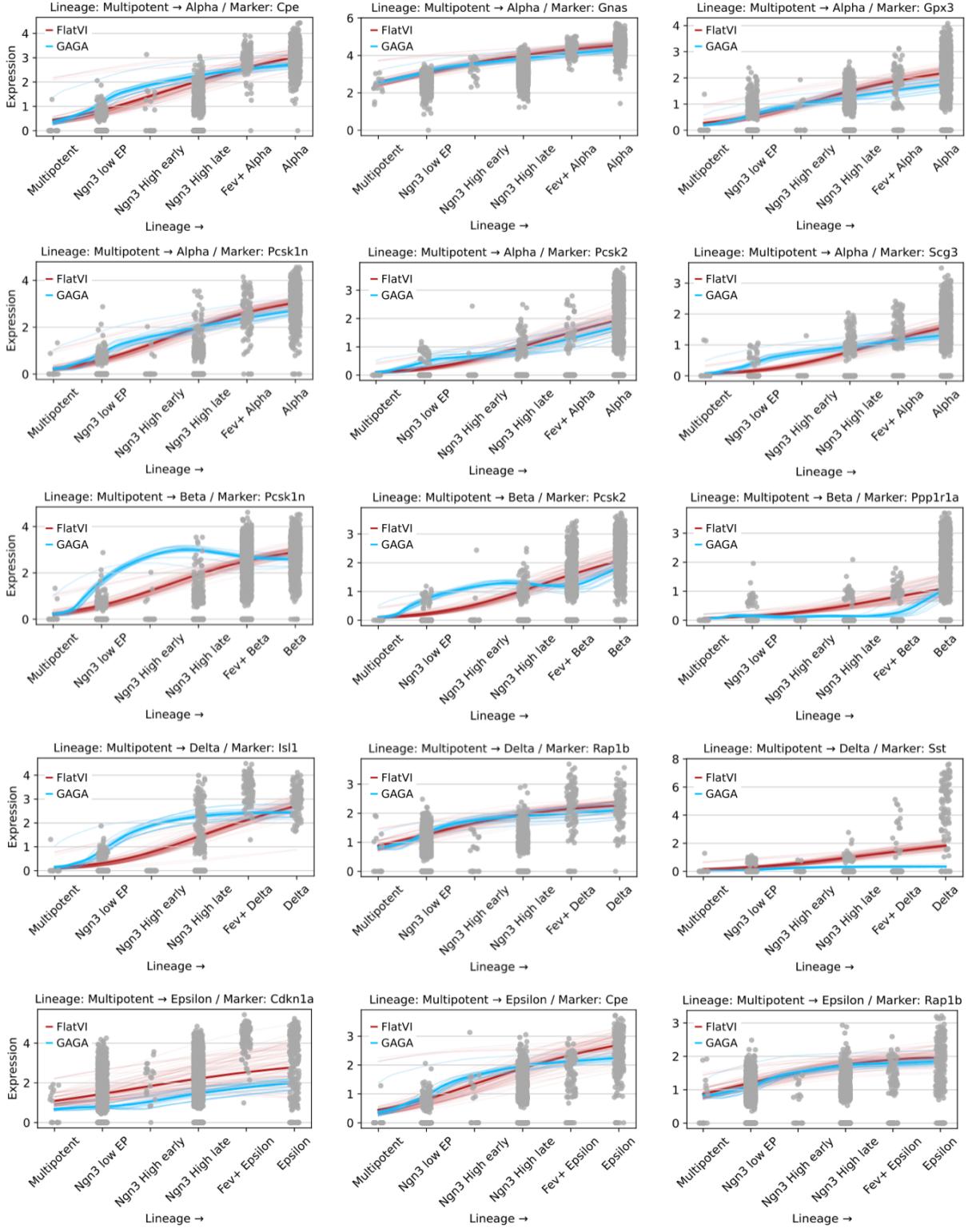
图 13: 插值路径上的基因表达趋势。红线 (FlatVI) 显示随着细胞成熟，标记基因的激活平滑且逼真。

如图 13 (以及论文中的图 5 )所示，FlatVI 为标记基因 (如 Cpe 和 Nnat) 产生了平滑、单调的趋势。这证实了在 FlatVI 潜在空间中的直线行走对应于平滑的生物学进程。

至关重要的是，由于 FlatVI 支持线性插值，它在计算上比需要求解微分方程来寻找测地线的方法要快得多。

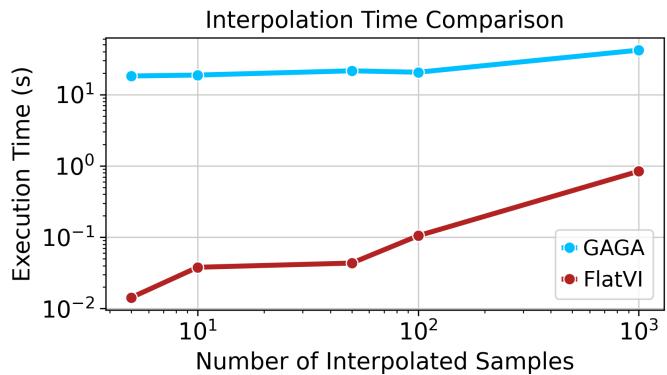
图 14: 计算效率。无论插值步骤的数量如何，FlatVI (红色) 都保持快速，而需要测地线求解器的方法 (GAGA，蓝色) 对于简单的寻路来说可能会更慢或实现起来更复杂。

关于图 14 的说明: * 虽然在这个特定图表中，对于小样本量，GAGA (蓝色) 在原始秒数上看起来更快，但 FlatVI 的关键优势在于操作的简单性*——简单的线性代数对比求解神经常微分方程。FlatVI 能够优雅地扩展，并允许在模型训练完成后即时生成路径。

结论与启示

FlatVI 代表了在确保我们的机器学习模型尊重其所代表数据的几何结构方面迈出的重要一步。通过将潜在空间正则化为局部欧几里得空间，作者实现了:

  1. 理论稳健性: 将潜在度量与负二项解码器的费雪信息度量对齐。
  2. 更好的动力学: 在最优传输轨迹推断中提高了性能。
  3. 可解释性: 使得简单的线性插值能够揭示复杂的生物学通路。

对于学生和研究人员来说，这篇论文强调了一个重要的教训: 架构不是一切；几何很重要。 你不能只是把数据塞进标准的 VAE 并假设潜在空间是有意义的。通过明确地强制执行几何约束——“拉平地图”——我们可以构建不仅在数学上严谨，而且在生物学上忠实的工具。

无论你是在模拟干细胞、癌症演化还是药物反应，知道你的“直线”实际上是最短路径，对于在复杂的生物学景观中导航来说，有着天壤之别。

参考文献与延伸阅读:

  • 本文基于 Palma, Rybakov 等人的论文 “Enforcing Latent Euclidean Geometry in Single-Cell VAEs for Manifold Interpolation” (2025)。
  • 本文中使用的图片直接摘自论文的图片集。