近十年来,一个幽灵一直萦绕在深度学习的殿堂: 对抗样本 。 这些输入 (通常是图像) 经过微小、人类难以察觉的扰动修改,却能完全欺骗最先进的神经网络。一张熊猫的照片,加上一点精心调整的噪声,在机器眼中就突然变成了一只长臂猿。
这种现象不仅是学术上的好奇心——它对部署在安全关键领域 (从自动驾驶汽车到医疗诊断) 的人工智能系统构成了严重威胁。尽管经过多年的深入研究,专家们仍在争论它为何会发生。这些漏洞究竟源于我们的训练方法、网络架构,还是更根本的机制?
最近的一篇论文《对抗样本不是 Bug,而是叠加态》 (“Adversarial Examples Are Not Bugs, They Are Superposition”) 提出了一个优雅而令人惊讶的解释。作者认为,对抗样本并非 bug,而是神经网络为提高效率而采用的一种技巧——叠加态 (superposition) ——的必然结果。叠加态这一概念源自机制可解释性研究,其核心思想是网络将多个概念或“特征”压缩进有限数量的神经元中。这种压缩极具威力,但也带来了代价: 干扰 (interference) ,一种内部串扰现象,而对抗性攻击正是利用了这种干扰。
让我们来剖析这个假设,并探索从简单的玩具模型到大型架构 (如 ResNet18) 中的证据。
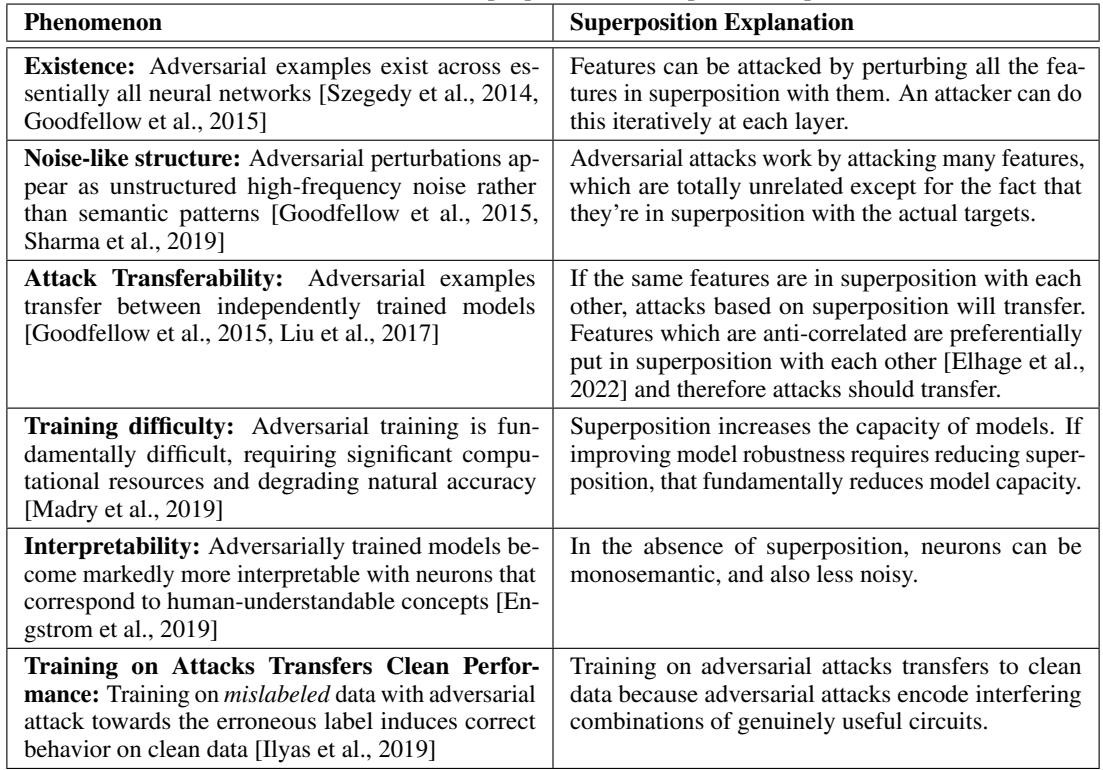
图 1: 六种持久的对抗样本现象以及叠加态提供的统一解释——从它们的存在性与噪声般的外观,到可迁移性和可解释性影响。
什么是叠加态?速读讲解
在进入实验之前,我们需要理解叠加态的概念。机制可解释性旨在对神经网络进行逆向工程,揭示其内部结构,将其视为可理解的系统,而非黑箱。在这一框架中,每个神经元的激活都代表了高维空间中的一个方向 , 该方向对应于模型学到的某个特征或概念。
想象一下,一个隐藏层的激活 \(h\) 可以表示为学习到的特征方向的加权和:
\[ h = \sum_{i < k} a_i \vec{f}_i + \vec{b} \]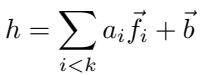
方程 1: 一层的激活值是学习到的特征方向的线性组合。
其中,\(k\) 是模型试图表示的特征数,\(a_i\) 是特征 \(i\) 的激活强度,\(\vec{f}_i\) 是对应特征的向量。
你可能认为,如果这个空间是 \(n\) 维的,那么该层最多只能表示 \(n\) 个正交特征——即网络的“容量”。但令人惊讶的是,神经网络通常可以表示远多于神经元数量的特征 (\(k > n\)) 。这是如何实现的?通过让特征方向重叠 。 这就是所谓的叠加态 。
叠加态是一种表征压缩形式,使模型能够捕捉远超过其规模所暗示的复杂结构。然而,特征重叠会引发干扰 : 激活一个特征时会部分激活其他特征。模型通常通过调整偏置项来在常规数据上抑制这种干扰,但在最坏情况下——例如对抗场景中——这种抑制机制将失效。
攻击者可以利用这种几何特性,精心构造输入以同时激活大量相互干扰的特征,从而在目标特征上产生显著的组合激活。这就是假设的核心: 对抗攻击是对叠加态引发的特征干扰的协同利用 。
证据一: 玩具模型中的因果关系
为了验证叠加态是否确实导致了对抗脆弱性,作者设计了一个可精确控制变量的简化“玩具模型”。他们的系统是一个小型自编码器,将 100 个输入特征压缩到 20 维隐藏空间中并重建输出。
调控叠加态: 稀疏性作为杠杆
当输入特征大多为非激活状态 (稀疏输入) 时,网络会学习重叠的表示——即叠加态——以高效利用有限的隐藏空间。当输入较密集时,则学习纯粹的一对一映射。因此,通过调整特征稀疏性 , 研究人员可以控制叠加态的强度。
为了测量叠加态,他们定义了“每维度特征数”的指标:
\[ \frac{\|W\|_F^2}{n} \]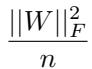
方程 2: 当该值超过 1 时,模型表示的特征数量超过神经元数量——表明存在活跃的叠加态。
为了测量对抗脆弱性 , 他们生成 \(L_2\) 范数有界的对抗样本以最大化重构误差:
\[ x_{adv} = x + \epsilon \cdot \arg \max_{\|\delta\|_2 \le 1} \mathcal{L}(x + \epsilon \delta) \]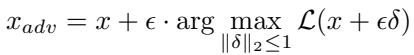
方程 3: 在固定扰动预算 \(\epsilon\) 内构建对抗样本。
实验 1: 叠加态影响鲁棒性
在第一个实验中,作者改变输入稀疏性以调整叠加态,观察模型的脆弱性变化。结果清晰无误: 稀疏性越高,叠加态越强,对抗脆弱性也越高。
结论: 直接增强叠加态会使模型更脆弱。 这是叠加态与对抗脆弱性之间的首个因果证据。
实验 2: 鲁棒性反过来抑制叠加态
为了探究双向因果性,团队反过来提问: 如果叠加态导致脆弱性,提升鲁棒性是否会减少叠加态?
他们采用了对抗训练 , 在损失函数中混合干净样本与被攻击样本:
\[ \mathcal{L}_{adv} = \alpha \cdot \mathcal{L}(x) + (1 - \alpha) \cdot \mathcal{L}(x_{adv}) \]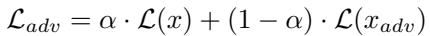
方程 4: 平衡干净样本性能与鲁棒性能的对抗训练目标。
结果令人瞩目。如下图所示,橙色线 (对抗训练模型) 始终表现出较低的叠加态和更高的鲁棒性,而蓝色线 (仅在干净数据训练的模型) 则相反。
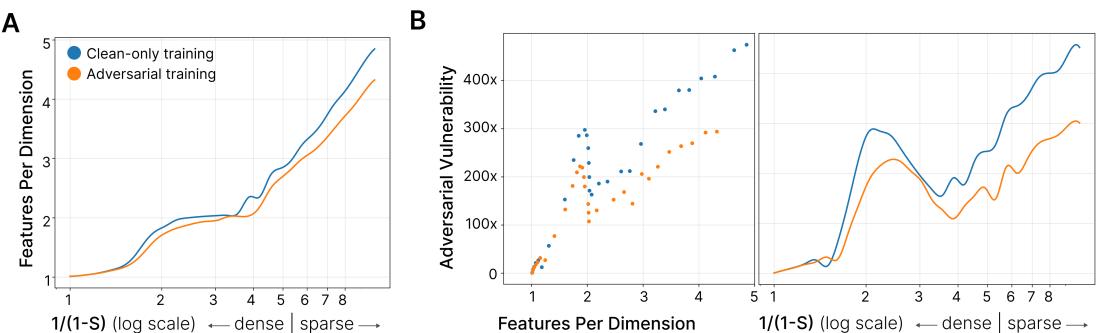
图 2: 对抗训练同时降低叠加态和脆弱性。干净训练的模型在叠加态增强时脆弱性急剧上升,而对抗训练模型保持稳定。
对抗训练改变了网络优化干扰的方式。标准训练最小化训练分布上的平均干扰:
\[ \min_{\boldsymbol{\theta}} \mathbb{E}_{(x,y)\sim\mathcal{D}}[I(x,y;\boldsymbol{\theta})] \]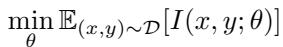
方程 5: 标准训练时的平均干扰最小化。
相比之下,对抗训练最小化潜在分布外样本的最坏情况干扰:
\[ \min_{\theta} \max_{\mathcal{D} \in \mathcal{D}_{\text{OOD}}} \mathbb{E}_{(x,y)\sim\mathcal{D}}[I(x,y;\theta)] \]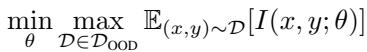
方程 6: 对抗训练中的最坏情况干扰最小化。
这种概念上的转变迫使网络修剪重叠的——也就是叠加的——特征表征,产生更孤立、更鲁棒的特征。
可视化攻击
为了观察叠加态几何结构的运行机制,作者可视化了特征干扰网络。节点代表特征,边的粗细对应 \((W_i \cdot W_j)^2\),即特征之间的干扰强度。

图 3: 对抗攻击激活了叠加态中的干扰特征。非鲁棒模型在对抗样本上表现为密集干扰网络,而鲁棒模型保持稀疏稳定。
在非鲁棒模型中,对抗输入会激活庞大的干扰网络,证明攻击利用了叠加态几何结构。而鲁棒模型则维持干净稳定的特征关系,抵抗扰动。
值得注意的是,对抗训练在减少叠加态的同时并未破坏特征的几何结构——只是修剪了重叠方向。
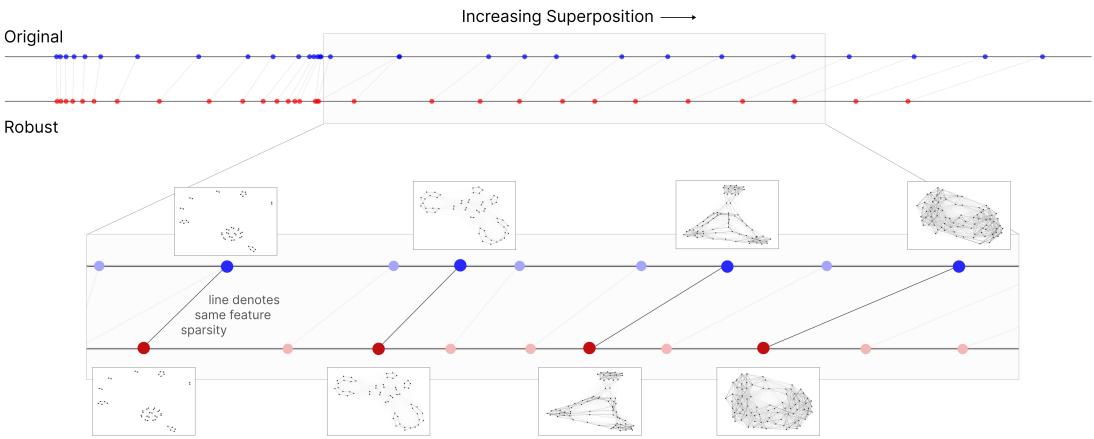
图 4: 鲁棒模型保留相似的特征几何,同时减少叠加态。线连接在相同稀疏度下训练的模型,展示结构一致性。
证据二: 从玩具模型到 ResNet18
玩具模型的发现意义深远——但它们能否推广到复杂的真实网络?
在大型模型 (如 ResNet18) 中,我们无法直接测量或操纵叠加态,因为真实的特征基不明确。为解决这一问题,研究人员在 ResNet18 的内部激活上训练了稀疏自编码器 (SAE) 。
SAE 的设计目标是分解叠加特征。如果模型的激活是高度叠加的,SAE 将难以重构,产生更高的损失。因此,更低的 SAE 重构损失表示叠加态更少 。
实验 3: ResNet18 的鲁棒性与 SAE 损失
作者在不同鲁棒性水平的 ResNet18 模型上训练 SAE。
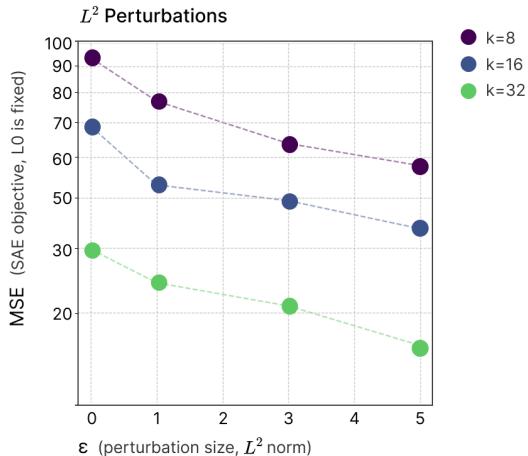
图 5: 更鲁棒的 ResNet18 模型呈现更低的 SAE 重构损失。不同稀疏度下的 TopK SAE 结果表现出鲁棒性 \((\epsilon)\) 与叠加态减少的系统性关联。
更鲁棒的网络 (在更强攻击下训练) 确实表现出更低的 SAE 重构误差——与玩具模型中的因果关系一致。对抗鲁棒性再次与叠加态减少相对应。
最后的证据: 攻击激活更多特征
如果对抗样本利用干扰,它们应触发更多特征。利用 SAE,作者测量了在不同攻击类型下被激活的特征数量 (即 \(L_0\) 范数) 。
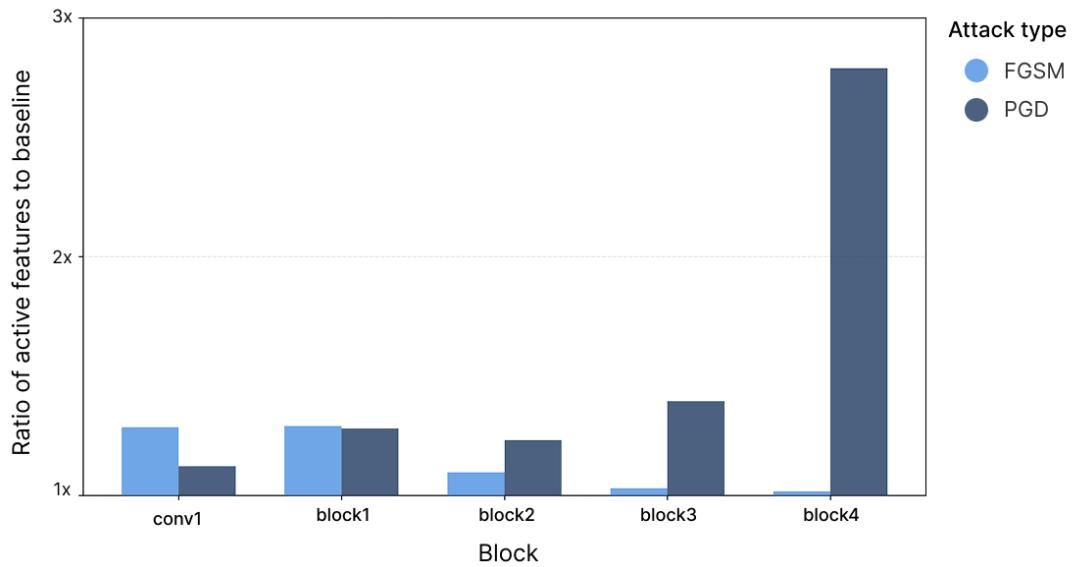
图 6: 对抗样本比干净输入激活更多特征。PGD 攻击在深层的激活接近基线的 \(2.8\times\)。
对抗攻击确实激活了更多特征——尤其是 PGD 攻击,在最后一层的激活数量接近基线的三倍。这种逐层放大效应与对抗样本利用连续叠加表征中的复合干扰的假设完全一致。
结论: 根本性权衡
无论是在玩具模型还是真实模型中,证据都指向一个深刻的事实: 对抗脆弱性与叠加态是同一枚硬币的两面。
叠加态让神经网络高效地在有限空间内打包数千个重叠特征,但这种效率本身也创造了可被对手利用的干扰通道。相比之下,对抗训练迫使网络解开重叠,降低叠加态,同时也降低表征效率。
由此揭示出一个根本的权衡:
- 更多叠加态 → 更高的效率与容量。
- 更少叠加态 → 更强的鲁棒性与可解释性。
换句话说,让模型更安全,也可能让它更易理解。这两个目标——面对攻击的鲁棒性和内部推理的透明度——或许共享同一条路径: 减少叠加态 。
正如论文标题所言,对抗样本不是 bug——它们是叠加态。
](https://deep-paper.org/en/paper/2508.17456/images/cover.png)