想象一下，你正在教一个机器人做一系列家务。首先，它学会了煮咖啡。接着，你教它如何烤面包。但在学会烤面包后，它完全忘记了怎么煮咖啡。更糟糕的是，随着你不断增加新任务，它会变得“卡住”，完全无法吸收新知识。

这就是持续学习 (continual learning) 的核心挑战——在这种设定下，人工智能系统从连续的数据流中学习，而不需要重访过去的样本。它面临两大障碍: 灾难性遗忘 (catastrophic forgetting) ，即丢失先前学到的技能；以及可塑性丧失 (loss of plasticity) ，即学习新内容的能力逐渐退化。

传统方法主要着眼于缓解遗忘，但保持可塑性仍然是一个更为难解的问题。有趣的是，最近的研究发现，由注意力机制驱动的 Transformer 架构在持续学习方面表现得异常出色。那么，究竟是什么让注意力如此有效？

一篇新的研究论文《Continual Learning with Query-Only Attention》提供了一个令人意外的洞见: 你可以舍弃注意力机制中的关键组成部分——键 (key) 和值 (value) ，只保留查询 (query) 。结果如何？一个更简单的模型不仅表现出竞争力，还增强了持续学习的能力。让我们来剖析这个极简主义理念的工作原理，以及它为何如此强大。

持续学习的双重挑战

要理解“仅查询注意力”的新颖性，我们首先需要了解其背景。

在标准训练中，模型会通过多个轮次 (epochs) 多次遍历整个数据集。相比之下，持续学习是顺序地接收数据——每个数据点只出现一次。随着新任务的到来，数据分布可能会发生变化，形成一个既动态又严苛的环境。

由此产生两个关键问题:

  1. 灾难性遗忘: 当模型在新任务上训练时，对参数的更新会覆盖掉先前学习的内容，导致旧任务性能显著下降。
  2. 可塑性丧失: 随着时间推移，模型的参数会收敛到损失函数的一个狭窄区域中。梯度流动变得微弱，使其难以对新任务进行适应。即使有新的数据，它也难以学习。

作者指出, 保持可塑性才是关键。如果一个系统能够维持其学习灵活性，那么遗忘将自然减少。

基础构件: 注意力、元学习和 kNN

在深入介绍具体方法之前，让我们回顾一下论文巧妙关联的三个基本概念。

1. 标准注意力

注意力机制使得像 Transformer 这样的模型能够在上下文中进行推理。它使用三类向量: 查询 (Q)、键 (K) 和 值 (V) 。 查询代表当前的关注点，键代表所有潜在的上下文项，而值承载相关信息。

每个查询都会与所有键进行比较——通常通过点积——来计算权重，这些权重决定对各值的关注程度。

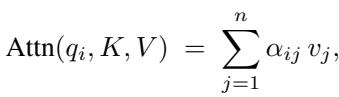
标准注意力机制计算值向量的加权和。

图: 在完整的注意力机制中，每个查询与所有键交互，以产生应用于相应值向量的权重。

权重通过对查询-键相似度进行 softmax 计算得到。

注意力权重是通过对查询-键点积进行 softmax 计算得出的。

图: 注意力权重放大相关信息，同时抑制无关信息。

对于一个长度为 \(n\) 的序列，该计算的复杂度为 \(O(n^2)\)。尽管功能强大，但在数据流快速到来的持续学习场景中，这种二次复杂度的成本可能过于昂贵。

2. 模型无关元学习 (MAML)

MAML 将学习视为一个跨任务的优化问题。它不是针对单个任务进行训练，而是寻找一个能够快速适应新任务的初始化状态。它交替进行内循环更新 (任务特定学习) 和外循环更新 (元层级调整) ，从而有效地“学习如何学习”。

3. k-最近邻 (kNN)

kNN 是一种经典方法，它通过对存储数据中最近邻的样本输出进行平均来预测结果。

k-最近邻的预测是最近的支持样本标签的局部平均值。

图: kNN 完全基于与存储样本的距离进行结果预测。

kNN 对灾难性遗忘免疫——它将知识以原始数据形式存储，而非不稳定的参数。然而，它缺乏跨任务的泛化能力。论文提出的仅查询方法通过结合数据驱动的适应性与学习到的相似性，弥合了这一缺口。

核心思想: 仅查询注意力

提出的仅查询注意力 (Query-Only Attention) 将完整的注意力机制精简到最核心部分。通过舍弃键和值，它以一个学习的函数 \(Q_\theta\) 来直接度量相似性，取代了查询-键交互。

其工作流程如下:

  1. 回放缓冲区: 维护一个内存缓冲区 \( \mathcal{B} \)，存储过去见过的样本 \((x, y)\)。
  2. 传入查询: 当新样本 \(x_t\) 到达时，将其视作查询。
  3. 采样支持集: 从缓冲区中抽取一个小支持集 \(S\) 作为上下文。
  4. 计算相似度分数: 对于支持集中的每个元素 \((x_j, y_j)\)，计算一个分数 \(d_j = Q_\theta(x_t, x_j, y_j)\)，作为学习到的相关性度量。
  5. 生成输出: 预测 \(\hat{y}_t = \sum_j d_j y_j\)，即支持标签的加权平均。

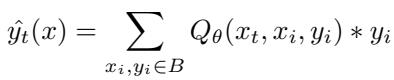
仅查询注意力的预测是支持集标签的加权和，其中权重由模型 Q-theta 学习得到。

图: 仅查询注意力通过学习到的加权函数，在查询与存储样本之间生成预测。

该模型相对于支持集大小的计算复杂度是线性的 \(O(n)\)，相比全注意力机制的 \(O(n^2)\) 可大幅提升效率。它能够处理更大的缓冲区，在保持轻量计算的同时提供更丰富的上下文。

终身学习的统一视角

作者进一步建立了一个概念性桥梁，将仅查询注意力、元学习和非参数模型串联起来。

全局学习 vs. 局部学习

传统的神经网络通过参数训练来适应每一个任务——这是局部解 。 后续任务会改变这些参数，从而导致遗忘。

仅查询注意力学习的是一个全局解 。 网络参数 \( \theta \) 定义的是一个通用的相似性函数，而非针对具体任务的解。任务适应在推理阶段动态发生: 预测依赖于上下文支持集，而非参数再优化。这是一种上下文内学习 (in-context) ，而非权重内学习 (in-weight) 。

一种可学习的 kNN 形式

该结构类似于加权 kNN，其中预测依赖于距离权重:

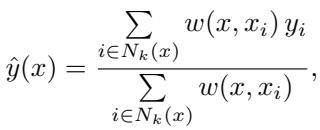
加权 kNN 使用一个权重函数 w(x, x_i)，该函数通常随距离的增加而减小。

图: 加权 kNN 使用固定、基于距离的权重来生成局部预测。

仅查询注意力通过函数 \(Q_\theta(x_t, x_i, y_i)\) 将这些固定权重转化为可学习的动态权重。这种灵活性使模型能够捕捉数据点之间复杂的关系，从而比传统 kNN 的人工距离度量提供更强的泛化能力。

隐式元学习

令人惊讶的是，仅查询注意力执行的操作类似于 MAML——它在推理时动态生成任务特定参数，而不是通过显式的梯度步骤。其预测可表述为:

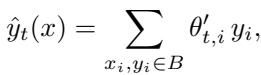
仅查询的预测可以看作是使用了即时生成的任务特定参数 theta-prime。

图: 每个查询隐式地生成其对应的任务特定权重，反映了元学习的自适应过程。

因此，仅查询注意力实现了“无内循环的元学习”，能够从缓冲区中存储的经验平滑地适应新任务。

实验与结果

论文在三个持续学习基准上评估了仅查询注意力方法，并与反向传播 (BP)、持续反向传播 (CBP)、全注意力 Transformer以及一个受 MAML 启发的变体进行了比较。

性能通过两个指标衡量:

  • 前向性能: 新数据上的准确率或损失；下降意味着可塑性丧失。
  • 后向性能: 旧数据上的准确率；下降则反映灾难性遗忘。

Permuted MNIST

每个任务都会随机重排 MNIST 的像素位置，迫使模型反复适应新的表示。

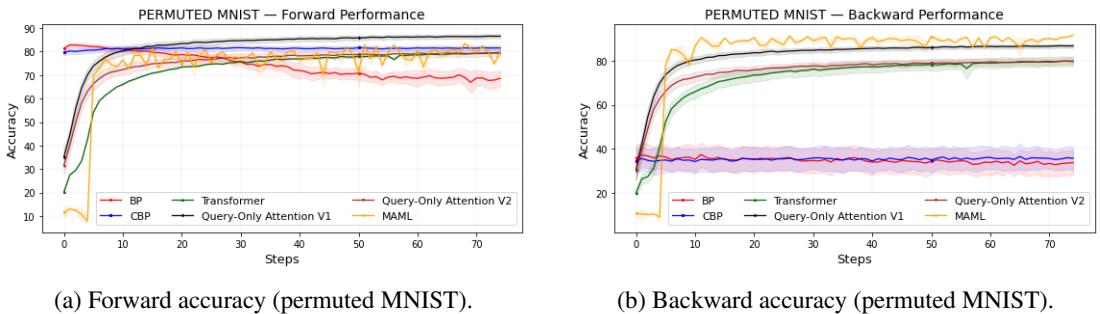
图 1: 在 Permuted MNIST 上的性能。y 轴显示准确率。仅查询注意力 (V1 和 V2) 以及全 Transformer 模型在前向 (可塑性) 与后向 (遗忘) 性能上均显著优于标准反向传播方法。

图 1: 在 7500 个任务中，仅查询注意力保持了强大的可塑性并有效抑制遗忘。

仅查询注意力的不同版本取得了与全注意力相当甚至更高的准确率，而 BP 的性能则显著退化。MAML 表现出色，但计算成本更高。

Split Tiny ImageNet

在此基准中，每个任务是从 Tiny ImageNet 的庞大类别集合中抽取的二分类任务。

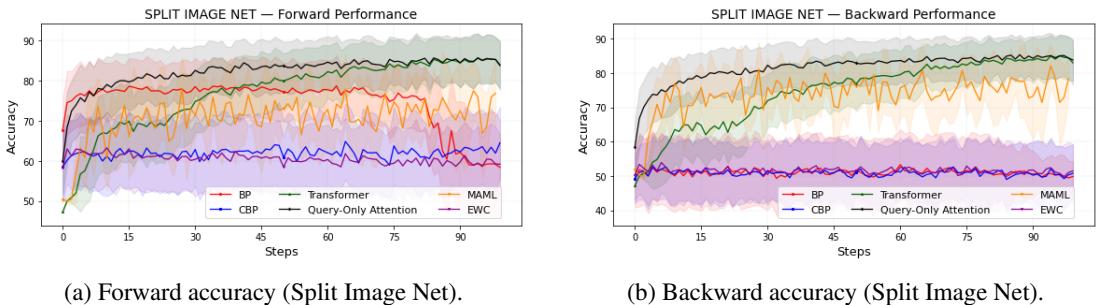
图 2: 在 Split ImageNet 上的性能。仅查询注意力和全 Transformer 模型再度表现出强劲而稳定的性能，而其他方法则困难重重，尤其在后向性能 (遗忘) 方面。

图 2: 仅查询注意力在复杂图像任务中高效扩展，同时保持前向和后向的准确率。

再度验证，仅查询注意力表现优异，超过了传统方法以及显式针对遗忘的基于 EWC 的基线。

缓慢变化回归 (SCR)

在该任务中，底层函数会逐渐发生漂移——这对模型的适应性提出了微妙的挑战。

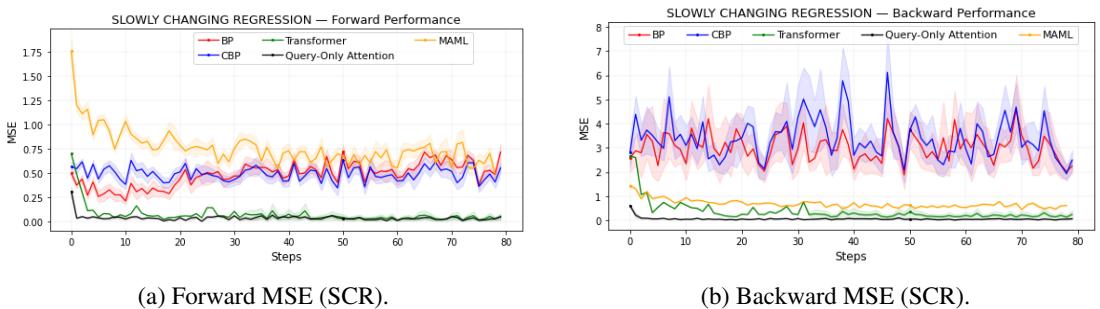
图 3: 在缓慢变化回归上的性能。y 轴显示均方误差 (MSE)，数值越低越好。仅查询注意力和 Transformer 保持较低误差，表明它们有效追踪了变化的数据分布。

图 3: 仅查询注意力在标准 BP 响应迟缓的情况下仍能保持低误差，稳健跟踪目标变化。

即使分布逐渐变化，仅查询注意力和 Transformer 模型依然保持低 MSE。BP 和 CBP 丧失了可塑性，而 MAML 变体虽更稳定但精度略弱。

深入探讨: 海森矩阵秩与可塑性

为探索学习稳定性的内部机制，作者分析了模型损失的海森矩阵 (Hessian matrix) ——这一工具刻画优化景观的曲率。具有高可塑性的模型呈现出丰富的曲率多样性，从而能够灵活转变学习方向。

海森矩阵的有效秩 (effective rank) 量化了这种多样性。高有效秩意味着广泛的学习能力；低有效秩则表明学习停滞。

海森矩阵的有效秩是其维度的度量，由特征值计算得出。

图: 有效秩捕捉了曲率的丰富程度——即可学习方向的维度“广度”。

实验证明，保持可塑性的模型通常也维持较高的有效秩。

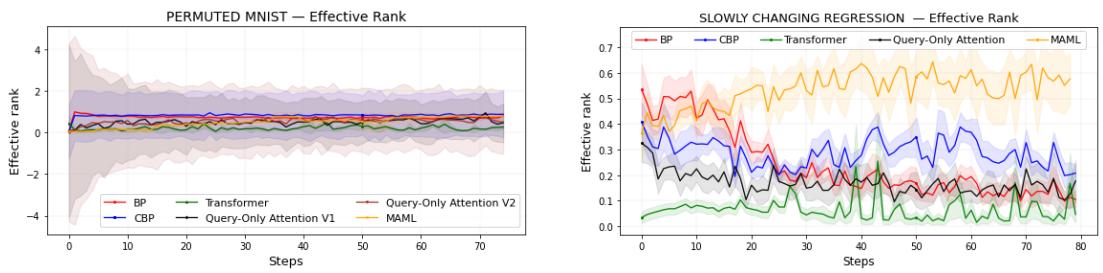
图 4: 在 Permuted MNIST 和 SCR 上的有效秩分析。保持可塑性的模型 (Transformer、仅查询注意力、MAML) 不仅稳定且具有高有效秩。标准 BP 模型的秩下降，与其学习灵活性的丧失一致。

图 4: 有效秩的下降对应可塑性的丧失；仅查询注意力展现出稳健的学习适应性。

这种相关性凸显了可塑性的几何本质——模型必须维持曲率多样性，才能在不断变化的任务中持续学习。

关键启示与展望

《Continual Learning with Query-Only Attention》这项研究在理论与实践上都取得了重要进展:

  1. 简约而强大: 去掉键和值并不会削弱学习，反而强化它。仅查询架构计算高效、具备强大可塑性。
  2. 统一框架: 该机制将注意力、元学习与基于记忆的模型融合在同一视角下，兼顾三者优点。
  3. 上下文中的元学习: 适应性在推理阶段自然发生，无需繁重的内循环更新。
  4. 曲率的重要性: 海森矩阵的经验分析揭示了有效秩与模型保持适应能力之间的紧密联系。

尽管对回放缓冲区的依赖仍是一个限制，但这项研究表明，持久学习并不需要复杂的架构。在追求终身学习系统的道路上——无论是机器人、智能体，还是不断进化的神经网络——一个简单的查询加一个智能的相似性函数或许就足够。

未来的持续学习，或许不在于记住一切，而在于懂得如何提出正确的问题。