FunLoRA：让 AI 永远学习而不遗忘的巧妙技巧

人工智能已经取得了非凡的成就——有时在复杂推理、视觉和创造性任务上甚至超越了人类。然而，大多数人工智能系统都存在一个人类本能掌握的根本弱点: 在不遗忘的情况下持续学习 。

当神经网络学习一项新任务时，它容易出现灾难性遗忘: 为新任务更新权重时，会抹去过去任务的表征。想象一下，学会了游泳却突然忘了如何骑自行车——这就是灾难性遗忘的真实体现。对于希望随时间不断进化的人工智能而言，这是一个严重的局限。

这一挑战对于生成式模型——图像合成、文本生成和艺术创作背后的引擎——尤为严峻，因为这些模型必须在众多概念中保持创造性的多样性。为每个新领域从头重新训练它们既昂贵又缓慢。传统的“回放”方法，即在混合新旧合成数据上再训练，只是暂时推迟问题。随着时间推移，它们的准确性和保真度都会下降——就像复印件的复印件一样。

最近，Victor Enescu 和 Hichem Sahbi 的研究论文 《使用函数式 LoRA 的深度生成式持续学习 (FunLoRA)》 提出了一个简洁而出人意料的简单机制来正面解决这一问题。 FunLoRA 使 AI 模型能够顺序学习而不遗忘，同时仅需极少的额外参数。它重新审视了已知的微调策略 LoRA，并赋予其函数式的新变化——这一变化可能从根本上改变生成模型的长期学习方式。

---

背景: 为什么持续学习如此困难

持续学习 (Continual Learning，CL) 旨在使模型能够在一系列任务上训练，同时不丢失已学信息。对于判别式分类器而言，挑战在于保持过去的决策边界稳定；而对生成式模型来说，这更为艰难——它们必须可靠地复现所有过去数据的分布。

早期的解决方案如样本回放，会存储旧数据或合成样本，但该方法的内存和隐私开销巨大。更先进的解决方案依赖生成式回放——即模型在生成的数据上重新训练——但这会导致收敛缓慢和质量下降。

FunLoRA 通过重新思考模型如何获得新能力，从根本上规避了这些问题。

---

流匹配: 更简单、更快速的生成过程

多数现代生成式模型——如 Stable Diffusion——基于扩散过程: 该过程向数据添加噪声，并通过数百个去噪步骤学习逆向转换。虽然能产生极高质量的结果，但速度十分缓慢。

FunLoRA 构建在条件流匹配 (Conditional Flow Matching，CFM) 之上，这是一种更快、更直接的生成技术。它学习一个向量场 \(v_{\theta}(t, \mathbf{x})\)，该向量场可以平滑地将噪声向量映射到真实图像，从而避免迭代去噪的繁琐过程。

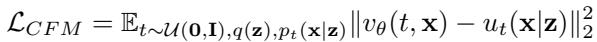
模型学习将其预测的速度场 \(v_{\theta}\) 与已知的条件目标场 \(u_t(\mathbf{x}|\mathbf{z})\) 对齐。

噪声与数据之间的概率路径定义如下:

\[ \mathbf{x} = (1 - t)\mathbf{x}_0 + t\mathbf{z} \]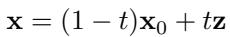

流匹配使用数据与噪声之间的直接线性插值，而非扩散模型的弯曲多步路径。

这种“直线路径”公式使采样过程快速且易处理，非常适合持续学习场景中高效生成大量图像的需求。

---

LoRA: 高效的模型微调方法

大型神经网络可能包含数十亿参数，使得完整微调既浪费又昂贵。 低秩适配 (Low-Rank Adaptation，LoRA) 通过冻结大部分权重，仅学习小规模的低秩扰动来解决这一问题。

LoRA 并非更新完整的权重矩阵 \(\mathbf{W}_0\)，而是学习一个残差 \(\Delta \mathbf{W}\)，该残差是两个窄矩阵 \(\mathbf{A}\) 与 \(\mathbf{B}\) 的乘积:

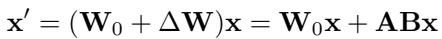
LoRA 将更新表示为 \(\Delta \mathbf{W} = \mathbf{A}\mathbf{B}\)。可学习参数数量显著减少。

在推理阶段，基础权重与其低秩修正项同时使用。这项技术极大改善了大型语言与视觉模型的高效适应方式——尤其适用于数据稀缺的设定。

---

FunLoRA: 函数式地扩展表达能力

传统 LoRA 虽强大，但存在一个限制: 表达能力取决于秩 (rank) 。 秩为 1 的矩阵 (最紧凑形式) 只能表达线性关系——节约但有限。FunLoRA 通过巧妙的数学变换函数式地提升秩，从而增强模型表达力。

1. 用于卷积层的 LoRA

标准 LoRA 多应用于 Transformer 的注意力层，而 U-Net——众多生成模型的核心结构——主要通过卷积处理类别与时间信息。因此，FunLoRA 将 LoRA 直接应用到卷积层。

对于每个类别标签 \(y\):

\[ \mathbf{F}_y = \mathbf{A}_y \mathbf{B}_y \]

其中 \(\mathbf{A}_y\) 与 \(\mathbf{B}_y\) 为秩 1 矩阵，并重塑为卷积滤波器相应维度。

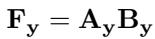
每个类别学习一对向量，其乘积形成 \(\mathbf{F}_y\)，即对应卷积滤波器的调制矩阵。

FunLoRA 不再将更新项加到 \(\mathbf{W}_0\) 上，而是采用逐元素乘法:

\[ \mathbf{W}_y = \mathbf{W}_0 \odot \mathbf{F}_y \]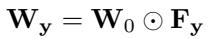

哈达玛 (逐元素) 积根据类别特定的函数矩阵重新缩放滤波器，同时保留原有骨干网络结构。

该方法为每个类别生成独立子网络，无需复制整个模型——实现任务间无干扰且无遗忘。

2. 函数式地提升秩

FunLoRA 的真正创新在于如何在不增加参数的情况下提升秩。它对 \(\mathbf{A}_y\) 与 \(\mathbf{B}_y\) 应用 \(p\) 个函数 \(f_i\)，并对输出求平均:

\[ \mathbf{F}_y = \frac{1}{p}\sum_{i=1}^{p}\alpha_i f_i(\mathbf{A}_y,\mathbf{B}_y) \]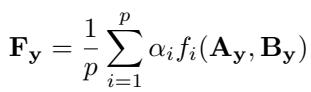

不同的非线性函数 \(f_i\) 丰富了 \(\mathbf{F}_y\) 的表达能力，却无需增加参数数量。

这些函数包括:

• 循环移位: 在乘法前重新排列向量元素。
• 逐元素幂: 应用如 \(x^1, x^2, \ldots, x^p\) 的幂操作。
• 三角函数: 使用不同频率的余弦波。

其中，三角函数效果最佳。余弦形式如下:

\[ f_i^{\cos}(x) = \cos(\omega_i x) \]

它学习不同频率 \(\omega_i\) 及其可训练权重 \(\alpha_i\)，实现具有周期性的调制，模拟更高秩的变换。

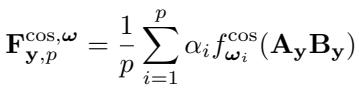
余弦函数通过引入基于频率的变化扩展并多样化有效秩。

该机制在整个 U-Net 中应用，为每个类别动态调节卷积层特性。

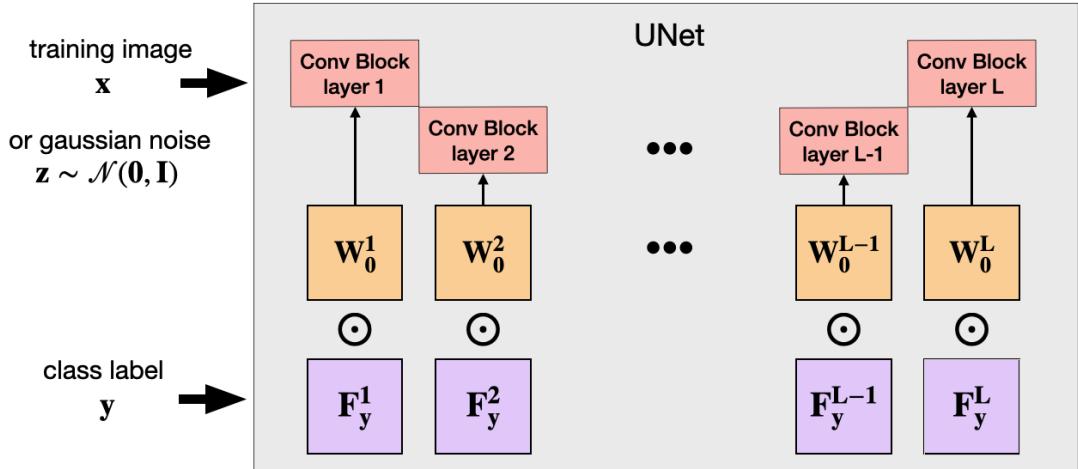
编码器与解码器路径中的卷积模块通过类别条件函数矩阵 \(\mathbf{F}_y^l\) 进行适配。

---

实验: FunLoRA 的表现

FunLoRA 在常用的持续学习基准上 (CIFAR10、CIFAR100、ImageNet100) 进行了测试，这些数据集被拆分为顺序任务，随着时间引入新类别。

识别关键层

并非所有层对适应性贡献相同。作者为每个卷积层计算了一个基于参数偏差的重要性得分。

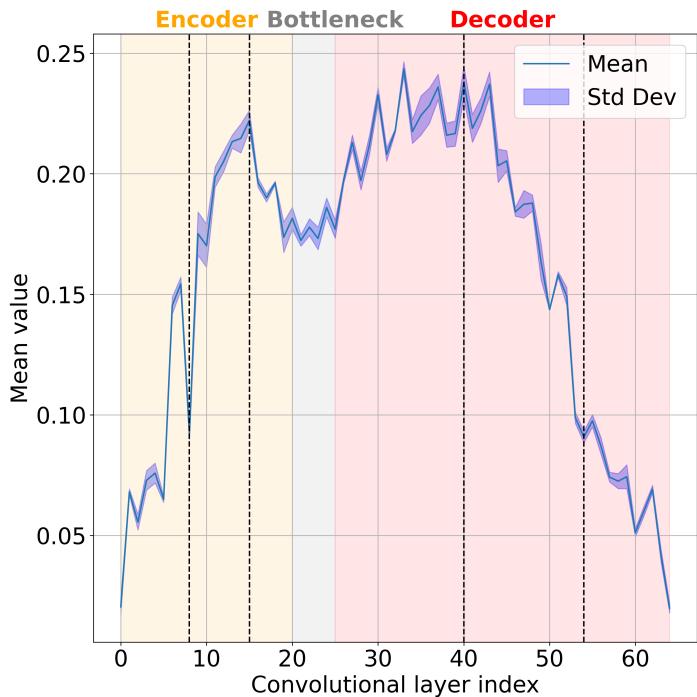
中间层与解码器层具有最高的重要性值，因此是 LoRA 适配的关键候选层。

仅关注索引 40–54 的层即可将参数数减少三倍，而准确率仅下降约两个百分点。这揭示了中层解码器层在类别适配中至关重要。

---

消融研究: 余弦函数的力量

在系统的消融实验中，基于余弦的函数式扩展在所有指标上均表现最佳，超越了传统 LoRA 的加法与乘法基线，即使这些基线使用更多参数。

所用函数	层索引	每类参数 ↓	最终准确率 ↑	平均增量准确率 ↑
原始 (加法)	0–64	35.59K	59.23	67.17
原始 (乘法)	0–64	35.59K	60.84	68.82
余弦 (可学习)	0–64	35.35K	61.82	69.18
原始 (加法)	40–54	11.26K	59.29	67.65
余弦 (可学习)	40–54	10.03K	60.07	68.06

在所有数据集中，余弦变体取得了最佳性能，同时保持极高的内存效率。

从直觉上看，余弦的振荡特性赋予模型灵活、局部的表达能力。其有效秩常超出函数数量上限 (\(p = 10\)) ，超越了幂或移位函数的限制。

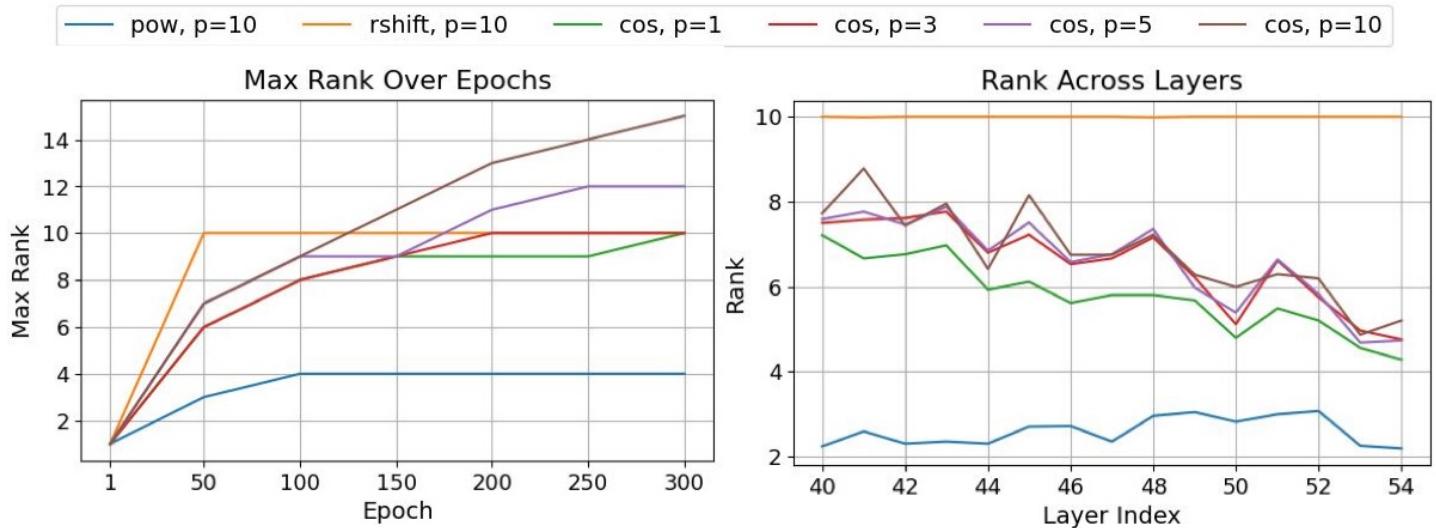
基于余弦的函数达到超过 \(p=10\) 的最大秩，产生更丰富的变换。

进一步分析发现，学习到的权重 \(\alpha_i\) 与频率 \(\omega_i\) 在层间的分布不同——早期层侧重中频以区分类别，后期层则偏低频以表征整体结构。

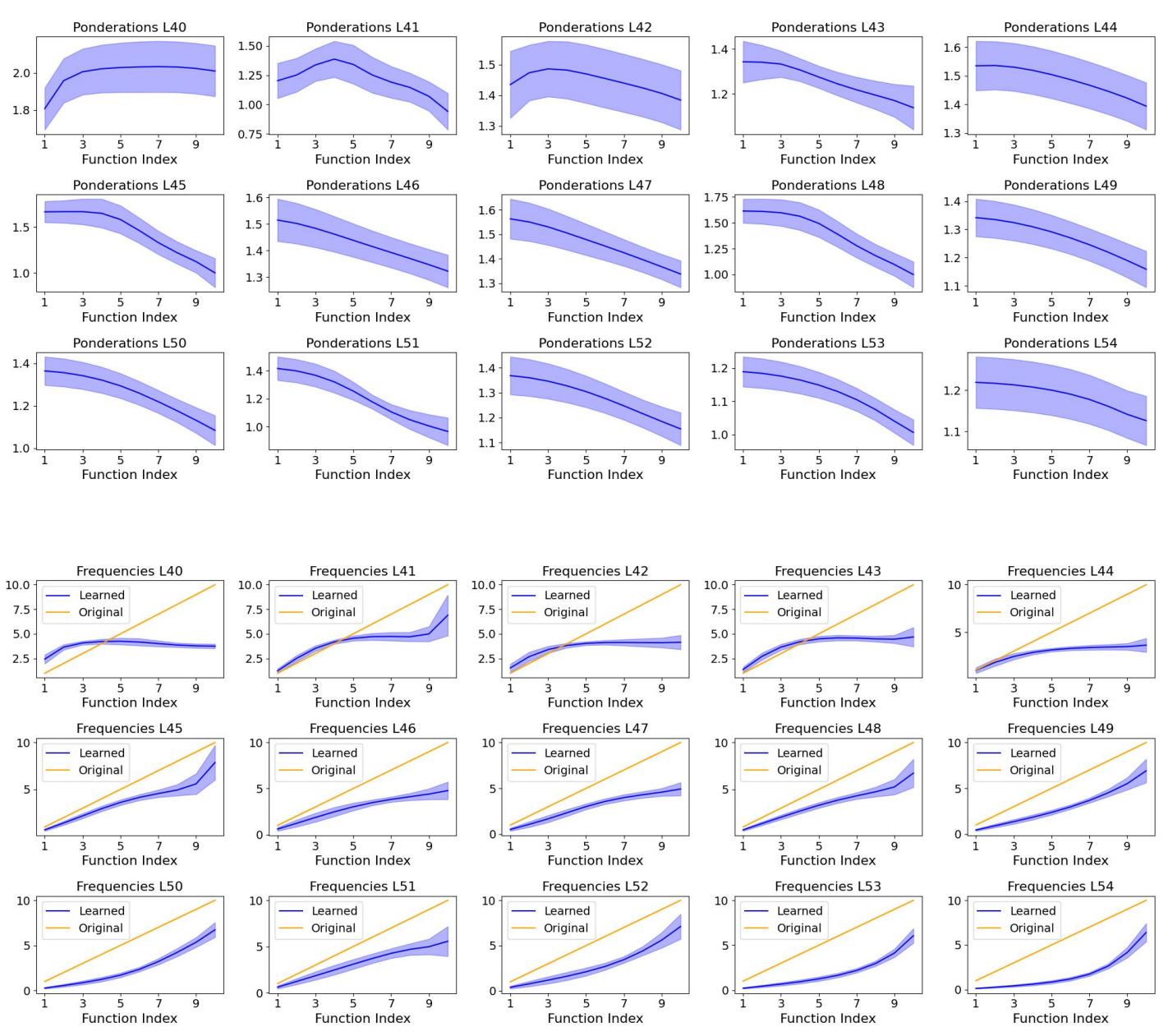
低频函数在输出层占主导，而中间层捕捉复杂的条件模式。

---

对比当前最优方法

FunLoRA 与主流持续生成方法 (DDGR、GUIDE、JDCL、DiffClass) 及使用大型预训练模型的变体进行了性能对比。

方法	CIFAR100 LA↑	ImageNet100 LA↑	骨干参数量
DDGR (Diffusion)	28.11	25.59	52.4M / 295M
GUIDE	41.66	39.07	52.4M / 295M
JDCL	47.95	54.53	52.4M / 295M
DiffClass (Stable Diffusion，预训练)	62.21	67.26	983M
FunLoRA (我们的)	60.07	58.30	36.6M / 90.7M
FunLoRA + 重采样	67.89	63.03	36.6M / 90.7M

尽管 FunLoRA 模型规模更小、速度更快且从零训练，其性能仍超越了大量训练的扩散替代方案。

令人瞩目的是，FunLoRA 的“重采样”版本 (生成额外合成数据) 在 CIFAR100 上甚至超越了 DiffClass——该方法基于拥有 9.83 亿参数的预训练 Stable Diffusion 模型。这证明了持续生成学习可以既紧凑又强大。

定性结果进一步说明了这一点。

增量学习与多任务训练生成的图像几乎无差异。

增量训练的 FunLoRA 完美保持了图像质量，证明没有灾难性遗忘。

---

FunLoRA 的意义

FunLoRA 重新定义了持续生成学习的效率:

• 无遗忘: 每个类别使用独立自适应参数，任务间无干扰。
• 参数极少: 每个类别仅需少量额外参数，即使任务成千上万也能轻松扩展。
• 高表达性: 函数式秩提升 (特别是余弦函数) 在极低内存占用下实现丰富变换。
• 高速度: 基于流匹配的训练与采样比扩散模型快数个数量级，实现实时适应。

FunLoRA 表明，持续学习并不依赖大型预训练模型或复杂的回放机制。通过函数式的巧妙设计，即使秩为 1 的结构也可动态演化成高度表达的终身学习者。

---

总结

FunLoRA 不仅是一个优化技巧，更是一种重塑神经网络适应性的思考方式。融合流匹配的速度、LoRA 的参数高效性，并在此基础上加入函数式创新，它实现了 AI 长久以来的愿望:

一个能够持续学习、永不遗忘所知的智能系统。

这标志着生成式 AI 向真正的终身学习迈出了关键一步。

---