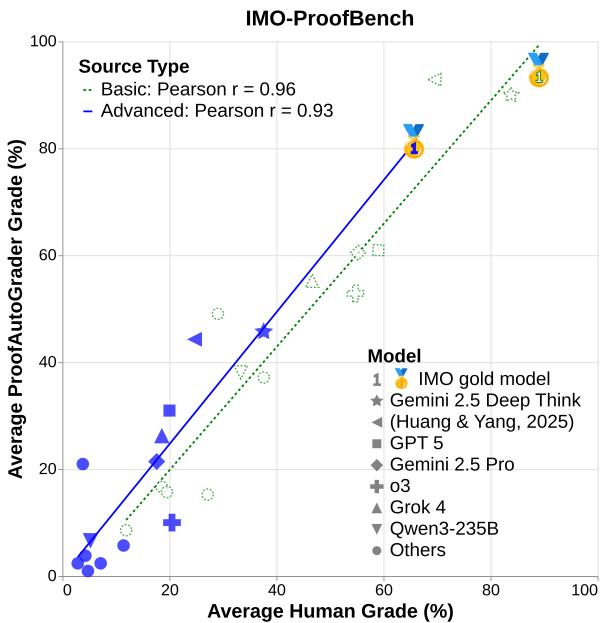
一张散点图，显示了在人类评分与自动评分之间对 AI 生成数学证明的高度相关性。

图 1 | IMO-ProofBench 上人类评分与自动评分之间的相关性。基础和高阶问题均显示出强一致性，表明自动化证明评估的可行性。

在构建更智能的人工智能系统的竞赛中，大型语言模型 (LLM) 在数学推理方面取得了惊人的进展。早期的基准测试，如 GSM8K 和 MATH , 曾一度设定了挑战的标准，但这些数据集如今已接近饱和。许多顶尖模型可以轻松通过它们，这让研究人员开始怀疑，这些测试衡量的究竟是真正的推理能力，还是仅仅是模式识别。

更深层次的问题在于，大多数数学基准测试只检查最终答案。这就像批改微积分试卷时只看最后方框里的数字，而忽略了得出该数字的整个推导过程。这种方式可能捕捉到的是猜测，而非真正的推理。

为了推动该领域向前发展，我们需要一个更严峻的挑战——一个既重视过程也重视结果的挑战。 IMO-Bench 应运而生，它在论文 “迈向稳健的数学推理” 中被提出。研究团队将目光投向了年轻数学家最艰难的竞技场: 国际数学奥林匹克竞赛 (IMO) 。

IMO 并非死记硬背的计算竞赛。其问题旨在考查独创性、创造力以及证明写作技能。通过建立 IMO 级别的 AI 基准测试，作者们希望将焦点从“得出正确答案”转向“证明其正确性”。本文将深入解析 IMO-Bench 的三个组成部分，探讨世界领先的 AI 模型的表现，并阐述该基准测试如何成为 AI 可靠、可验证推理能力的转折点。

为什么选择国际数学奥林匹克竞赛？

在介绍基准测试之前，有必要先问: 为什么 IMO 是评估 AI 推理的理想基础？

与许多专注于公式化解题或记忆的数据集不同，IMO 问题需要创造力。它们常常需要跨越代数、几何、数论、组合数学等多个领域，融合概念并提出全新的解决步骤——这些步骤往往从未在教学中出现。其目标不仅仅是计算，而是在压力下的创造性逻辑。

这正是它成为稳健推理的重要试验场的原因。为了构建 IMO-Bench，作者们与一组 IMO 奖牌得主合作，他们负责审查题目并制定评分标准，以确保严谨、公平与挑战性。

IMO-Bench 套件包含三个不同的基准测试，每一个都针对推理的特定方面。

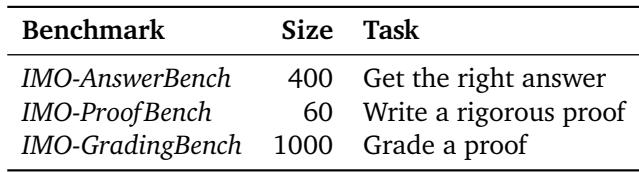
一张表格，展示了 IMO-Bench 套件中的三个基准测试: IMO-AnswerBench、IMO-ProofBench 和 IMO-GradingBench。

表 1 | IMO-Bench 的三大支柱: 简答准确性、证明写作能力和评分能力。

第一部分: IMO-AnswerBench — 模型能找到正确答案吗？

第一个组成部分 IMO-AnswerBench 包含 400 道奥林匹克风格的问题，这些问题都有简短、可验证的答案。该阶段评估模型在无需明确证明的情况下，进行奥林匹克级别推理并计算精确结果的能力。

问题选择与多样性

这些问题涵盖了竞赛数学的四个经典领域——代数 (Algebra)、组合数学 (Combinatorics)、几何 (Geometry) 和 数论 (Number Theory)——每个领域各有 100 个例题。难度范围从初中水平的准 IMO 问题到真正的 IMO 第 3 题或第 6 题级别挑战。

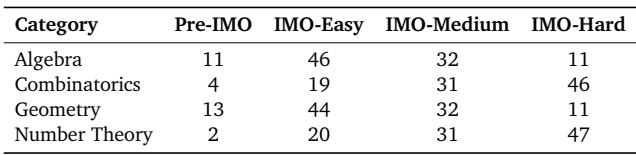
一张表格，展示了 IMO-AnswerBench 中四个类别问题的难度分布。

表 2 | IMO-AnswerBench 各数学领域的难度分布。

这种多样性确保了该基准不仅测试计算能力，也体现概念广度。如下图，不同领域的题目分布差异显著: 几何更侧重于角度和边长计算，而数论与组合数学则挑战模型的抽象推理。

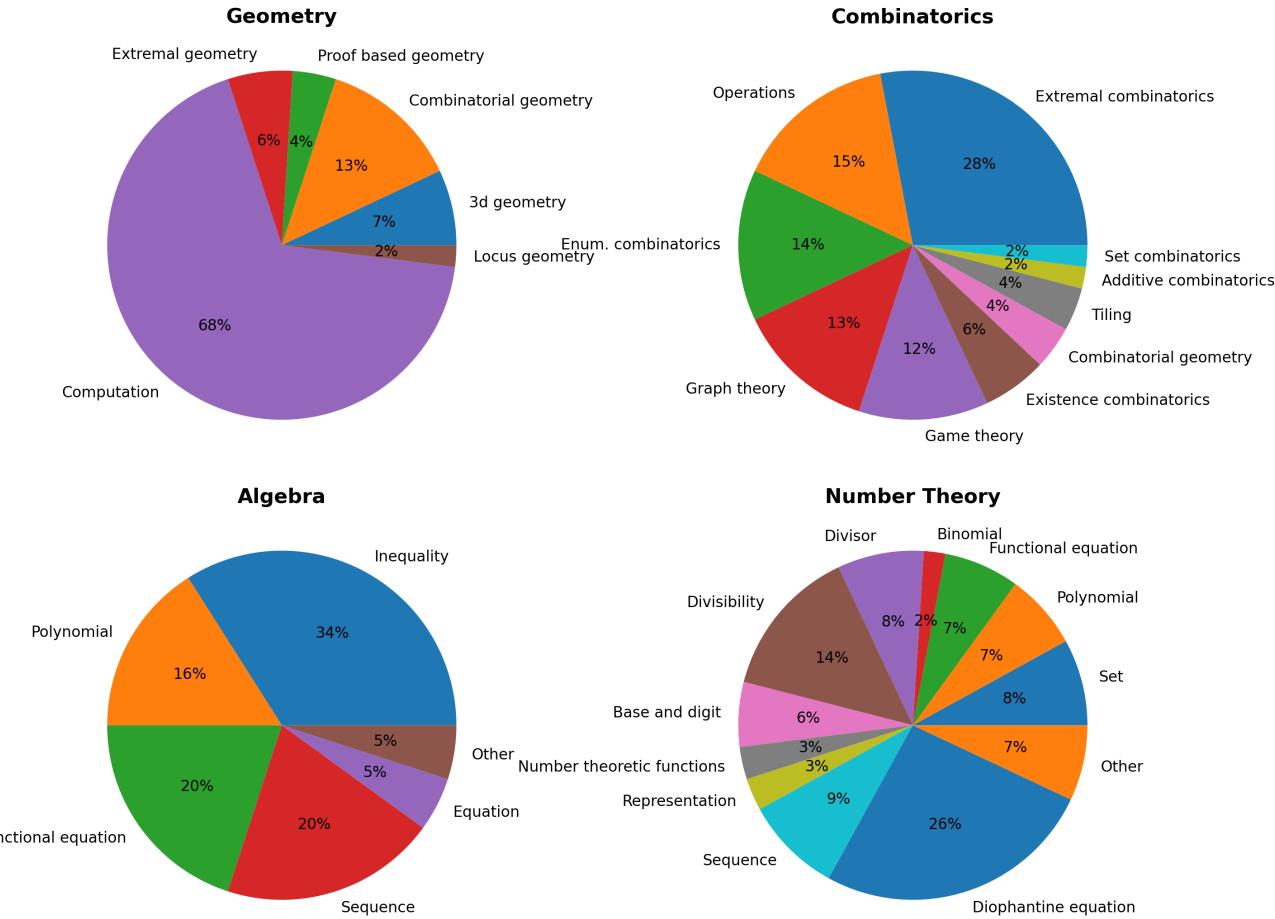
四张饼图，展示了 IMO-AnswerBench 中几何、组合数学、代数和数论的主题分布。

图 2 | 按领域划分的主题分布。数论与组合数学囊括了最广泛的子主题，对模型的抽象推理能力提出了更高要求。

使基准测试“稳健”

公共基准测试通常面临一个臭名昭著的问题: 数据污染 。 如果模型在训练阶段见过相同的题目或解法，其表现就无法反映真实的推理能力。

为解决该问题，作者提出了名为 问题稳健化 (Problem Robustification) 的多步骤机制，改造原有奥林匹克题目，包括:

  • 改写语言与结构
  • 更改变量 (例如在几何题中重命名点)
  • 修改数值以减少记忆效应
  • 添加干扰项——增加认知负荷的无关成分
  • 重新表述方程但保留核心逻辑

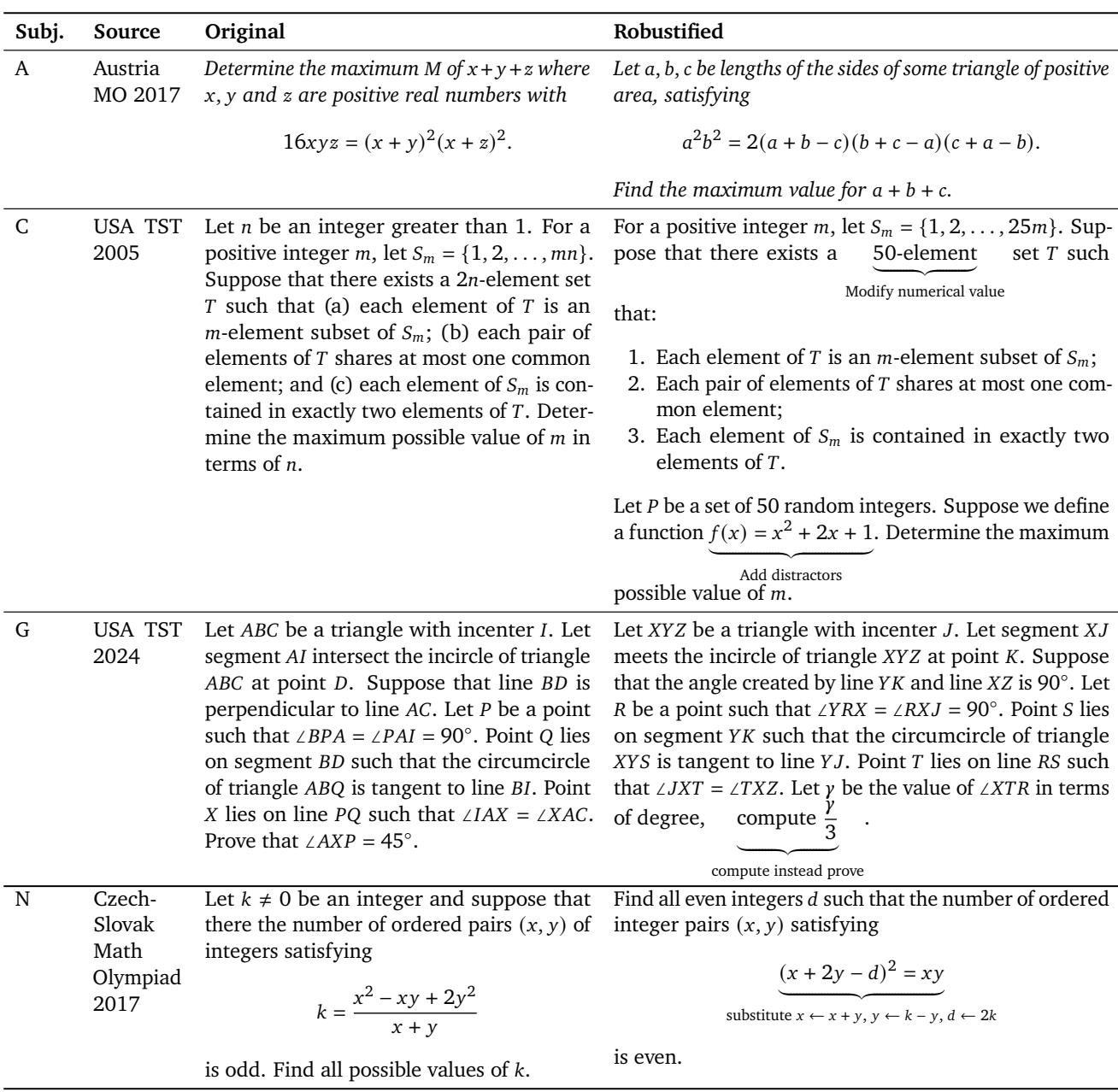
奥林匹克竞赛原题及其在 IMO-AnswerBench 中“稳健化”版本示例。

表 8 | 奥林匹克题目重构示例，以防止记忆并促使模型从第一性原理进行推理。

自动化评分: AnswerAutoGrader

即便是简短答案，自动评分也很棘手。例如，人类知道“除 -4 以外的所有实数”等价于 \((-∞, -4) ∪ (-4, ∞)\)，但脚本可能判定为不同。

为此，论文提出了由 Gemini 2.5 Pro 驱动的 **AnswerAutoGrader **。 该模型通过语义提取与验证机制评估答案的数学等价性，而非仅仅比对文本。结果显示，其评分与人类几乎完全一致，使得在保证准确性的同时实现大规模评估成为可能。

第二部分: IMO-ProofBench — 推理能力的真正考验

得到一个正确的数字是一回事，但 AI 能证明为什么这个数字正确吗？

IMO-ProofBench 正是对此进行考验。每道题都要求给出完整、逻辑严密、用自然语言撰写的证明。仅有正确答案而无正确推理不能得分。

该基准包含 **60 个基于证明的任务 **, 分为两个级别:

  1. **基础集 (30 题): ** 准 IMO 至中等难度，用于基础评估。
  2. **高阶集 (30 题): ** 奥数级挑战，包括 5 套完整的 IMO 风格题集与 18 道奖牌得主编写的新题，以确保原创性。

证明如何评分？

非正式证明的评估充满主观性。为标准化，研究者采用了 IMO 官方的 7 分制，并简化为四个类别。

一张表格，展示了简化后的 IMO 评分系统，包含四类: 正确、几乎正确、部分正确和不正确。

表 3 | IMO-ProofBench 使用的简化四级评分标准。

虽然人类专家是金标准，但人工评分耗时漫长。团队构建了 ProofAutoGrader——一个基于 LLM 的自动评分器。它接收题目、模型给出的证明、参考解答及评分指南，并输出详细评估。

尽管尚不完美，ProofAutoGrader 展现出强大潜力——其相关性分数接近人类水平，后文将展示结果。

第三部分: IMO-GradingBench — 模型能评判其他模型吗？

最后一项任务反转了角色: 模型不再是解题者，而是成为**评审者 **。

IMO-GradingBench 包含来自不同模型的 **1000 份证明提交 **, 均由专家数学家人工评分。模型需阅读题目与解答，并给出四级评分: 正确 (Correct)、几乎正确 (Almost)、部分正确 (Partial) 或不正确 (Incorrect)。

该基准测试评估模型对数学推理本身的理解能力。它能识别有效逻辑吗？能察觉细微但致命的错误吗？

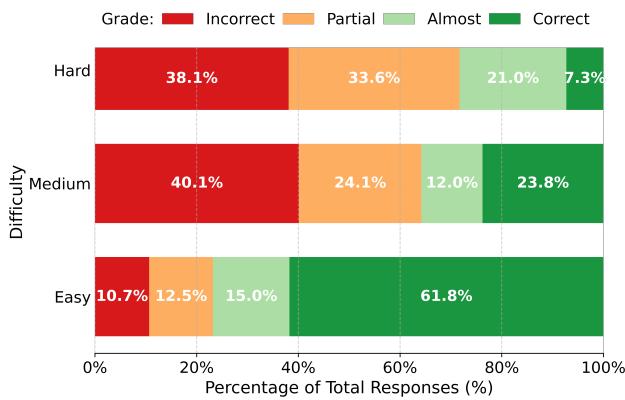
一张堆叠条形图，展示了 IMO-GradingBench 中不同难度下的评分分布。

图 3 | IMO-GradingBench 中的人类评分分布。难度越高，错误与部分正确的比例越高。

结果: 当今模型的表现如何

研究团队测试了多种公开与专有模型，结果揭示了当前的真实进展。

IMO-AnswerBench — 明显的领跑者

Gemini Deep Think (IMO Gold) 以卓越的 80.0% 准确率领先，在简答题基准中超越所有竞争模型。

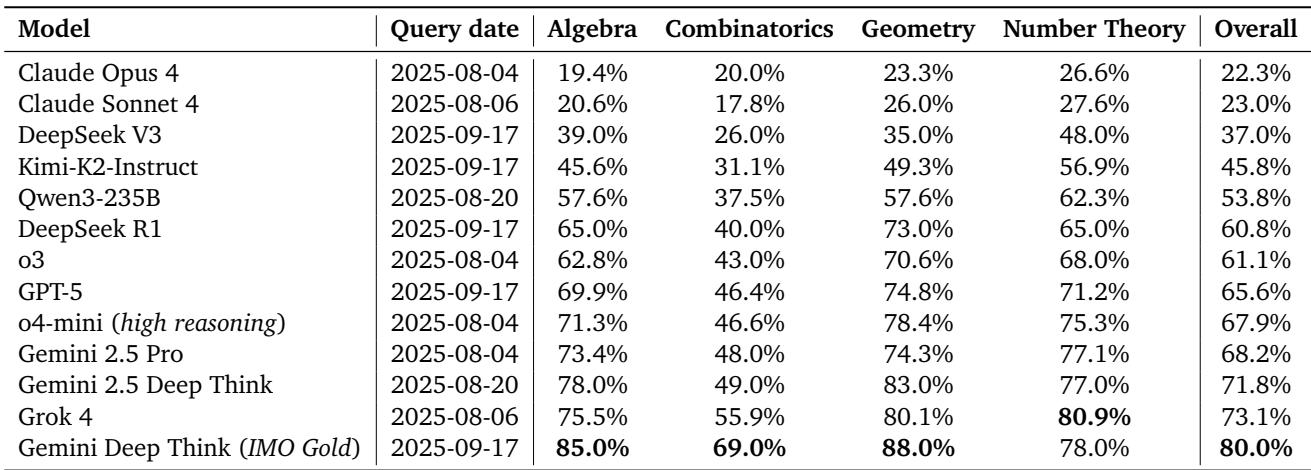
一张表格，按类别展示各 AI 模型在 IMO-AnswerBench 上的准确率。

表 4 | IMO-AnswerBench 各模型准确率表现。Gemini Deep Think 在所有领域均领先。

关键发现:

  • Gemini Deep Think 比 Grok 4 (非 Gemini 模型最佳) 高出 6.9%，比 DeepSeek R1 (开放权重模型最佳) 高出 19.2%。
  • 组合数学仍是大多数模型的薄弱环节，显示抽象组合逻辑的持久挑战。
  • AnswerAutoGrader 与人类评分一致率达 98.9%，验证了完全自动评分的可靠性。

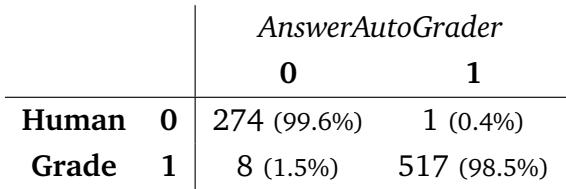
一个混淆矩阵，显示 AnswerAutoGrader 与人类评分的高度一致。

表 5 | 简答题的自动评分结果与人工评分几乎完全一致。

IMO-ProofBench — 巨大的分水岭

从答案到证明，模型间的性能差距急剧扩大。

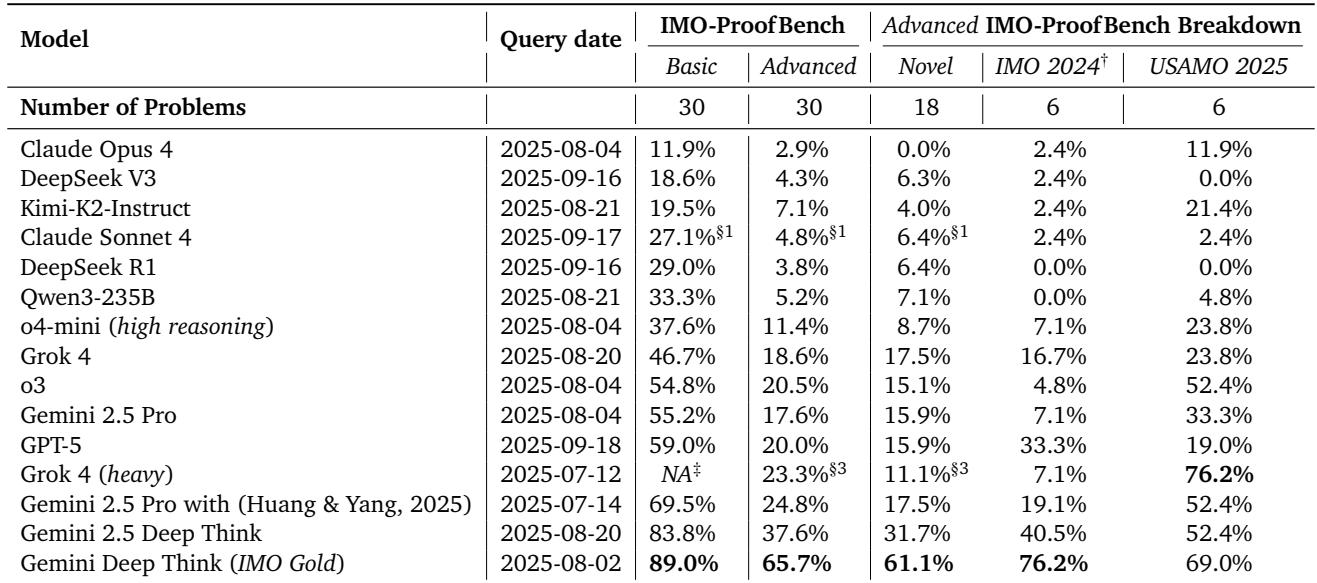
一张表格，展示了专家对各模型在 IMO-ProofBench 基础与高阶子集的评估结果。

表 6 | IMO-ProofBench 上的专家评估结果。多数模型未能在奥数难度下生成严谨证明。

观察结果:

  • 基础集中仅少数模型超过 50%，Gemini Deep Think (IMO Gold) 达到 **89.0% **。
  • 高阶集中，非 Gemini 模型均跌至 25% 以下，而 IMO Gold 达到 **65.7% **, 领先幅度达 42.4%。
  • 按题型分解可见潜在过拟合: Grok 4 在熟悉的 USAMO 2025 题上表现良好，但在新题上显著下降。Gemini Deep Think 表现稳定，显示出真实泛化能力。

ProofAutoGrader 的表现如何？

作者将 ProofAutoGrader 的成绩与专家人工评分进行了对比。

在公开模型测试中:

  • **皮尔逊相关系数 **: 基础集 0.96，高阶集 0.93
  • 在 170 个内部模型上:** r = 0.87 **, 即使推理质量差异较大，仍保持强相关性

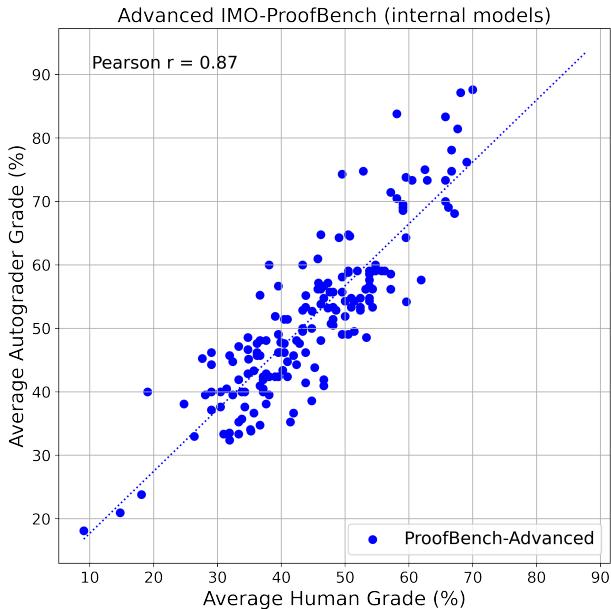
一张散点图，显示 ProofAutoGrader 与人类专家在内部模型评分之间的高相关性 (Pearson r = 0.87)。

图 4 | ProofAutoGrader 与人类评估在内部模型上的一致性。

大多数分歧出现于相近等级之间 (不正确 vs. 部分正确) 。

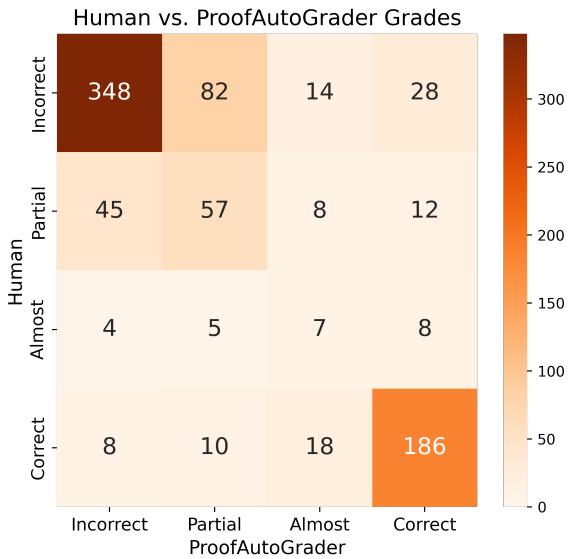
一个混淆矩阵，显示 ProofAutoGrader 最常见的错误分类发生在“不正确”和“部分正确”之间。

图 5 | ProofAutoGrader 的常见错误分类。即使接近人类水平，在相近评分间区分仍最具挑战性。

总体而言，ProofAutoGrader 证明了可扩展的证明评估可行。对于关键性评估仍建议人工复核，但自动化推理评估的基础已牢固建立。

IMO-GradingBench — 元推理的前沿

该基准挑战模型在无参考解答的情况下为他人证明评分，需要高度理解力。

一张表格，展示各模型在 IMO-GradingBench 上的准确率与平均绝对误差 (MAE)。

表 7 | 各模型在 IMO-GradingBench 上的表现。准确率 (%) 越高越好；平均绝对误差 (MAE) 越低越好。

关键观察:

  • 最佳准确率 (o3) 为 **54.0% **, 总体结果凸显此挑战的艰难性。
  • Gemini Deep Think (IMO Gold) 取得最低 MAE (18.4%)，展现更优的细粒度判断。
  • IMO-GradingBench 显示，评估数学推理本身是一项前沿挑战——理解证明比撰写证明更难。

结论: 为 AI 推理设立更高标准

IMO-Bench 为评估 AI 数学能力树立了新的黄金标准。它不再只奖励最终答案，而是衡量创造性推理与形式正确性——正是区分真正理解与猜测的关键。

主要结论:

  1. **推理差距确实存在。 ** 擅长找答案的模型往往在写证明时失利。IMO-ProofBench 清晰揭示了这一差异。
  2. **稳健性至关重要。 ** 通过改写和修改题目，IMO-Bench 有效防止死记硬背，确保测试衡量的是真实推理。
  3. **可扩展评估成为可能。 ** 借助 AnswerAutoGrader 与 ProofAutoGrader，可靠的自动评估可实现并补充人类专业判断。

随着 IMO-Bench 的公开发布，研究社区获得了一个严谨、透明的工具来衡量真正的数学推理能力。随着 AI 向通用智能迈进，前行之路或许正穿越与人类奥赛选手相同的领域——数学的创造性前沿。

挑战已然设定，接下来，是时候让模型证明自己了。