数学史是一部思想的发展史——闪烁的直觉、艰辛的探索与严密的证明构成了它的主线。如今，一类新型工具正开始拓展这一故事: 它们能够搜索、提出假设，甚至建议证明。AlphaEvolve，正是论文《大规模的数学探索与发现》的研究主题之一。它将大语言模型 (LLM) 的生成能力与进化式程序搜索和严谨的自动化验证相结合，最终形成一个能够在数十个数学问题上提出、测试和改进构造的智能体——有时能匹配现有的最佳已知解，有时能改进它们，偶尔还能提出启发人类证明的一般模式。

本文将介绍 AlphaEvolve 是什么、它为何有效，以及它产生的一些最具启发性的数学成果。我们将重点聚焦于直觉、可复现的方法论和具体示例，使具有数学背景的读者——无论是学生、研究人员还是从业者——都能理解这些系统的构建方式，以及如何使用或改进它们。

目录

  • AlphaEvolve 试图做什么 (以及不做什么)
  • 核心思想: 代码进化、搜索启发式与泛化器
  • 进化循环与“搜索模式”
  • 从实验到定理: 结合证明助手的工作流程
  • 实践权衡: 计算资源、模型选择与验证器
  • 精选数学案例
  • 有限域 Kakeya 和 Nikodym 构造
  • 自相关不等式 (奇异的极值函数)
  • Kakeya 针与类堆积构造
  • 堆积问题与人机协作
  • 其他一些速胜与惜败
  • 局限性、潜在问题与最佳实践
  • 简要路线图: 未来的研究方向

AlphaEvolve 试图做什么 (以及不做什么)

AlphaEvolve 是一个用于探索和构造的工具，专为生成具有强极值性质的显式数学对象的问题而设计: 例如，边多但禁止某类子图的图、能量最优的点配置、和集或差集极端的离散集合、堆积问题等。它不是一个通用的定理证明器 (虽然可以成为包含证明系统在内的工作流程的一部分) ，也不是一个能神奇地找到理论突破的黑箱。其优势在于大规模、半自动化、创造性的数值与程序探索——进化出能生成构造的程序，或进化出能快速找到构造的搜索启发式。

为什么选择程序空间？

一个核心洞见是，许多优雅的构造都有简短的程序描述形式。在短程序的空间中搜索——而不是直接在候选对象的组合空间中搜索——往往更容易获得结构化、可解释且稳健的解，同时避免陷入没有清晰描述的组合复杂性沼泽。

举例而言: 与其在所有 50 个顶点的图 (每个由 1225 位比特表示) 上搜索，不如搜索生成它们的简短 Python 程序。一次 LLM 的“变异”即可生成一族相关的程序，它们往往生成同类或相似的高质量图。这是一种寻找优雅解的更佳方式，比起将每个图当作独立数据点更自然有效。

核心思想: 代码进化、搜索启发式与泛化器

AlphaEvolve 建立在两种互补技术之上:

  1. LLM 参与的程序进化 : 进化中的“变异”由 LLM 生成，生成的是语法正确、语义合理的代码修改，比随机编辑更加智能；LLM 利用自身的代码与数学知识提出有意义的改动。

  2. 搜索模式的启发式算法 : 当验证器 (即评估器) 相对廉价时，AlphaEvolve 会进化出可在内部执行搜索的程序。换言之，它进化的是搜索启发式: 这类程序在给定时间预算下，通过快速局部搜索、随机重启、贪心移动或基于梯度的过程寻找优质对象。一旦这种启发式被进化出来，一次昂贵的 LLM 调用即可摊销为大量廉价的评估。

此外，还有一种 “泛化器模式” : AlphaEvolve 被要求生成一个在多种输入规模 (例如不同 n) 下表现稳定的程序，而非单一的实例构造。通过观察小规模实例，系统可识别模式并生成紧凑的通用算法或公式。

进化循环与“搜索模式”

系统运行过程按代进行:

  • 维护一组程序 (候选者) 。
  • 选择表现优异者作为 LLM 变异的种子。
  • 由 LLM 生成变异后代程序 (智能编辑) 。
  • 对每个后代运行验证器 (适应度函数) 。在搜索模式下，后代程序本身会执行大量廉价评估。
  • 保留表现最佳者并重复。

为什么“搜索模式”很重要

LLM 查询相对昂贵。如果验证器在一次 LLM 变异所需的时间内能评估数百万个候选者，那么让程序仅输出一个候选者是低效的。在搜索模式下，每个进化出的程序可运行时间受限的搜索，以廉价生成大量候选，系统根据其发现的最佳结果评分。这建立了乘数效应: 一次昂贵的 LLM 调用 → 多次廉价的数值搜索。

此外，它还能启发动态特化: 早期启发式偏重探索，后期偏重优化。整个进化过程往往形成一条“专门化启发式链”，组合后可生成出色构造。

泛化器模式: 从实例到公式

搜索模式关注单实例优化；泛化器模式则关注模式识别。实际运行中，AlphaEvolve 会在多个 n 值上进行评估，以综合得分 (如平均归一化质量) 推动程序实现泛化。此类成果尤为有趣: AlphaEvolve 能提出跨输入规模的紧凑算法或参数化构造，随后人类研究者 (或其他 AI 工具) 可将这些想法形式化或推广。

AI 工作流程: 发现、证明与验证

一个递进式的工作流程如下:

  • 模式发现 (AlphaEvolve) : 提出一个在多个输入下表现优异的程序化构造；
  • 符号推理 (Deep Think) : 为观察到的性质推导出证明或封闭形式表达；
  • 形式化验证 (AlphaProof + Lean/mathlib) : 将符号推理转化为完全形式化的证明。

这一流程在有限域 Kakeya/Nikodym 实验中已成功展示。AlphaEvolve 生成程序化构造，Deep Think 推导公式并给出证明，AlphaProof 则在 Lean 中形式化验证。AlphaEvolve 擅于提出候选，其他系统擅于符号与形式推理，两者协同实现从数值发现到正式定理的过渡。

实践权衡: 计算资源、模型选择与验证器

论文中包含详尽的消融实验与元分析，核心经验如下。

计算资源 vs. 求解时间

更多的并行 CPU 或 GPU 能更快获得成果，但会增加总 LLM 调用次数与成本。例如，在一个自相关不等式问题 (6.2) 中，使用 20 个 CPU 的运行比用 2 个 CPU 的运行更快获得优于当前最佳的界限，但调用次数更多、成本也更高。

模型选择: 大型 vs. 小型 LLM

更强大的 LLM 能生成高质量的程序变异，用更少的变异步数达到优解；然而，廉价模型能带来探索多样性。某些问题上，重复运行廉价模型 (低成本高多样性) 在实现最先进数值界限上更有效。结构复杂、理论性强的问题则需要顶级 LLM 才表现突出。

验证器设计

验证器 (适应度函数) 至关重要。设计不当会被“钻空子”: 程序可能通过数值误差或近似漏洞获得虚假高分。建议:

  • 优先采用连续、信息丰富的损失函数而非脆弱的离散惩罚，以保持梯度平滑、防止停滞；
  • 在发现阶段后，用高精度或严格验证器复检候选结果 (如使用有理运算或区间算术验证近似等式) 。

精选数学案例

AlphaEvolve 已在组合学、几何、分析与数论的 67 个问题上实验。以下选出几类代表性示例。

正面对比概览 (视觉总结)

一张表格对比 FunSearch 与 AlphaEvolve 的特性。AlphaEvolve 能进化任何语言数百行代码文件、支持加速器上的长时间评估、利用最先进的 LLM 并使用丰富上下文，而 FunSearch 范围更有限。

对比: FunSearch vs. AlphaEvolve——程序范围、评估规模与对 LLM 依赖性。

1) 有限域 Kakeya 与 Nikodym 构造 (泛化器模式)

问题简述 : 在 \(\mathbf{F}_q^d\) 中，Kakeya 集包含每个方向的一条直线；Nikodym 集 \(N\) 要求任意点 \(x\) 都在某条位于 \(N \cup \{x\}\) 的直线之上。渐近上，最小 Kakeya 集大小约为 \(\approx q^d/2^{d-1}\)；改善低阶项常涉及微妙的数论技巧。

AlphaEvolve 的结果 : 使用泛化器模式，它在多个素数 \(p\) 上提出程序化构造。对 \(d=3\)，它重新发现并略微改进了已知构造: 对于 \(p \equiv 1 \pmod 4\)，生成了大小为

\[ \frac{1}{4}p^3 + \frac{7}{8}p^2 - \frac{1}{8} \]

的 Kakeya 集，主项与文献一致、低阶项略有优化。Deep Think 随后分析出封闭形式公式，并由 AlphaProof 在 Lean 中形式化验证其正确性。

为何值得注意 : 构造中涉及二次剩余与多项式约束等数论结构，而 AlphaEvolve 未显式提供参考却发现了正确形式，展现其在具有深层算术结构问题上也具备探索能力。

2) 自相关不等式: 高度不规则的极值函数

自相关问题关注卷积 \(f * f\) 的近似能力或范数界限。极值可能呈现高度不规则甚至分形状。

问题 6.2 与 6.3 : AlphaEvolve 搜索分段常数函数 (固定划分) ，进化启发式扰动系数并结合梯度步与回溯。它将问题 6.2 的上界降低至 \(1.5032\)，并生成高质量反例函数。对于问题 6.3，结合梯度法与进化启发式，生成了含 50,000 段的阶梯函数，将下界提升至 \(0.961\)。这些极值函数结构极度不规则，反映了仅靠人类直觉或简单梯度优化难以探索此类复杂空间。

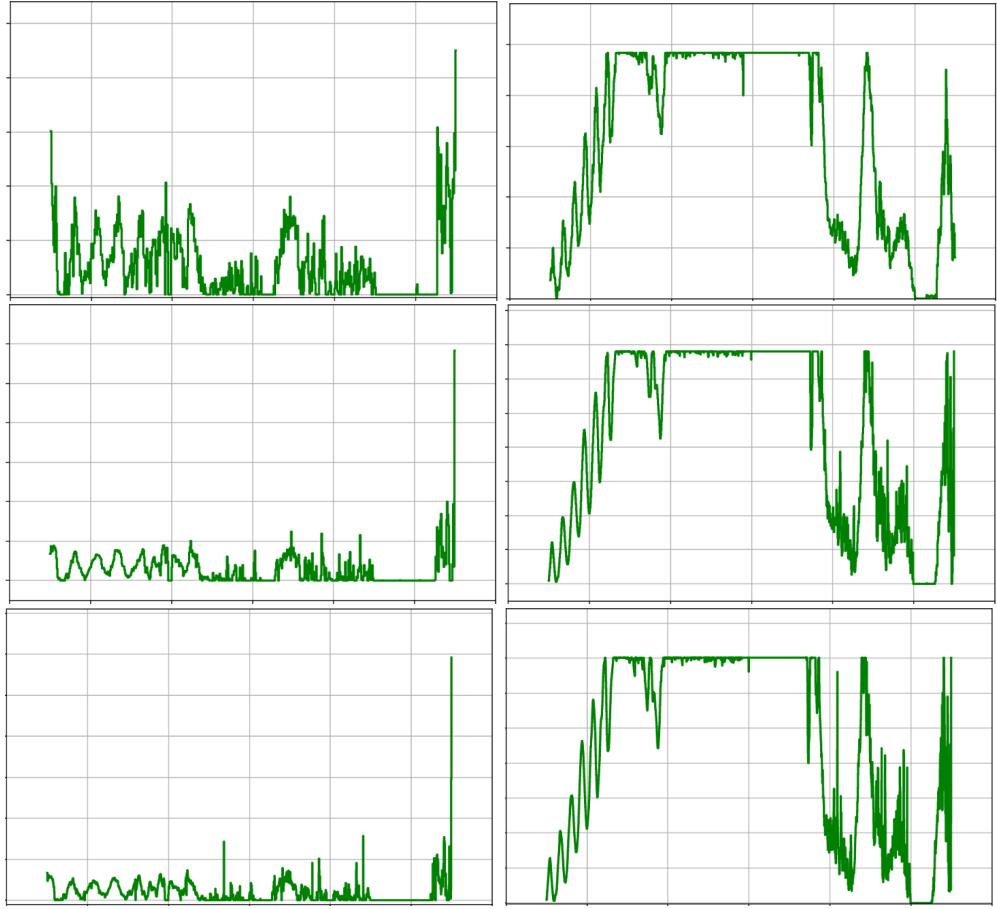
左图: AlphaEvolve 为自相关问题发现的三个高度不规则、尖峰状的函数。右图: 它们复杂的自卷积结果。

为问题 6.2 构造的阶梯函数及其自卷积——高度不规则，难以解析。

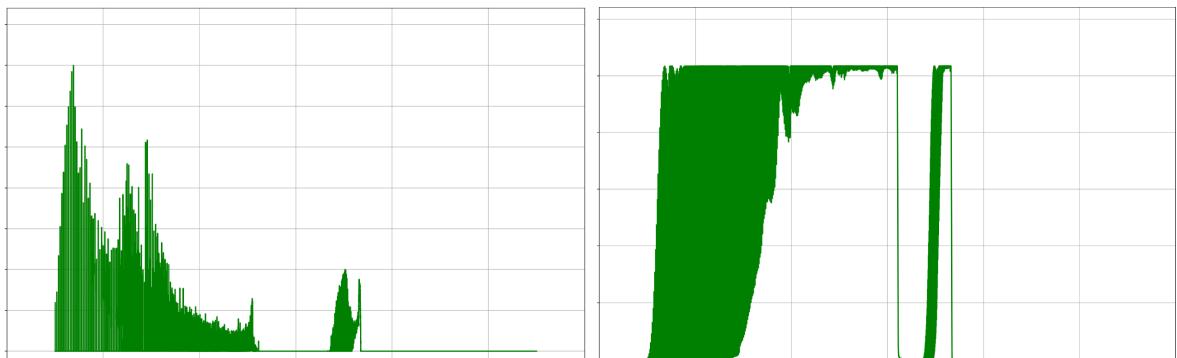
左图: 另一个自相关问题的最佳构造，一个由 50,000 个分段组成的高度不规则函数。右图: 其自卷积。

AlphaEvolve 发现的 50,000 阶梯分段函数，改进了问题 6.3 的下界。

3) Kakeya 针问题 (几何优化)

问题简述 : Kakeya 针问题 (Besicovitch) 询问旋转单位线段 360° 所需的最小面积。其离散形式为: 指定 \(n\) 后，如何摆放 \(n\) 个三角形或平行四边形，以最小化并集面积或最大化相关评分。

AlphaEvolve 的结果 : 在搜索模式下，它进化启发式生成放置方案。多数 \(n\) 情况下，其布局比 Keich 构造更小的并集面积。进一步泛化时，它发现了捕捉 Keich 式位运算构造并推广到非 2 的幂次 \(n\) 的紧凑算法。构造虽不如经典方案规则或自相似，却在数值上普遍优越。

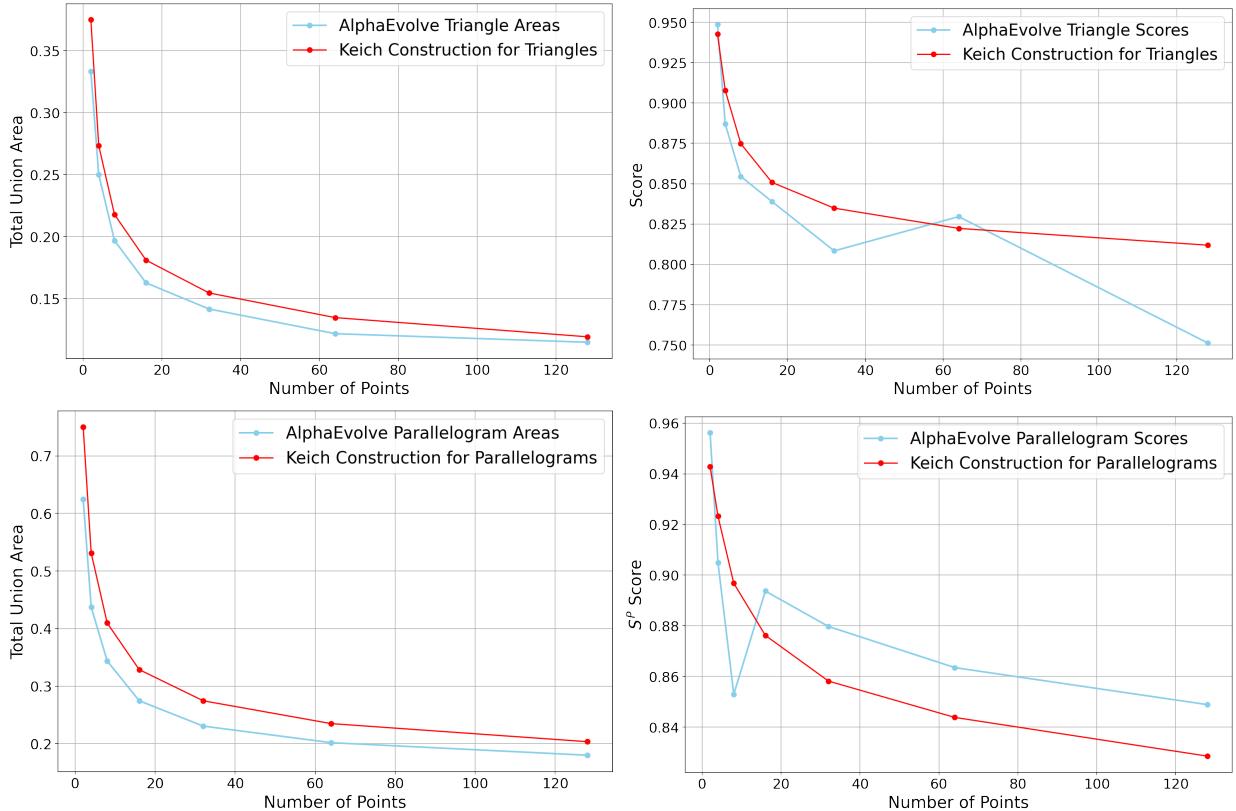
AlphaEvolve 对 Kakeya 针问题的构造与 Keich 的方案对比。AlphaEvolve 一致找到并集面积更小的配置。

左: 总面积与 n (三角形/平行四边形) 关系。右: 性能评分对比 (AlphaEvolve vs. Keich) 。

Kakeya 问题的平行四边形构造可视化: 上排为规则的 Keich 构造，下排为不规则但性能更好的 AlphaEvolve 构造。

Keich 构造 (上) 与 AlphaEvolve 构造 (下) 在不同 \(n\) 值下的比较。

4) 堆积问题与人机协作

AlphaEvolve 研究了多种堆积问题——圆形在方形中堆积、六边形在大六边形中堆积、单位立方体在大立方体中堆积等。这类问题可视化强，适合搜索模式的启发式 (随机初始 + 局部松弛) 。

显著成果及协作示例:

  • 六边形堆积 : 改善了在大六边形内堆积 11 与 12 单位六边形的最佳已知排列。人类专家进一步调整对称性后获得最终最优解——体现了“AI 探索 + 人类精修”的合作模式。
  • 立方体堆积 : 将 11 个单位立方体堆入大立方体的上界改进至边长约 \(2.895\)，创造新纪录。

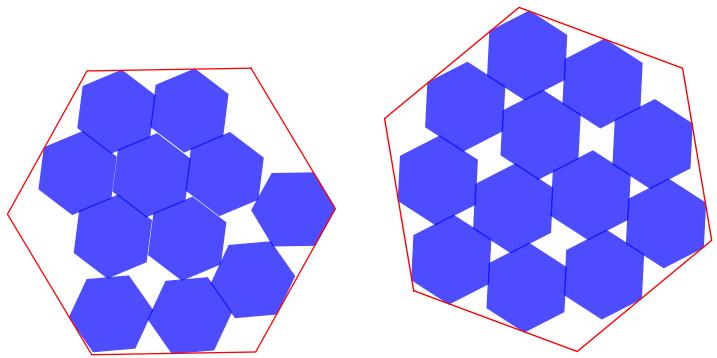
AlphaEvolve 发现的在大六边形中堆积 11 与 12 单位六边形的破纪录构型。

AlphaEvolve 优化后的六边形堆积 (11、12) 。

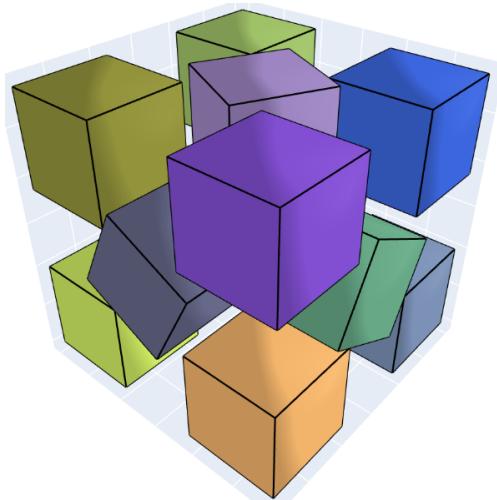
边长约 2.895 的大立方体中堆积 11 单位立方体的新纪录。

改进的 \(n=11\) 立方体堆积。

5) 积木堆叠与泛化 (教学型示例)

积木堆叠 (悬臂) 问题的经典结果: \(n\) 个单位积木最大悬臂为 \(\tfrac{1}{2}H_n\)，其中 \(H_n\) 为第 \(n\) 个调和数。AlphaEvolve 使用泛化器模式，找到有限 \(n\) 的最优堆叠、推测递推规律，进而形成调和公式程序。这展示了系统如何从小实例数据抽象出一般规律。

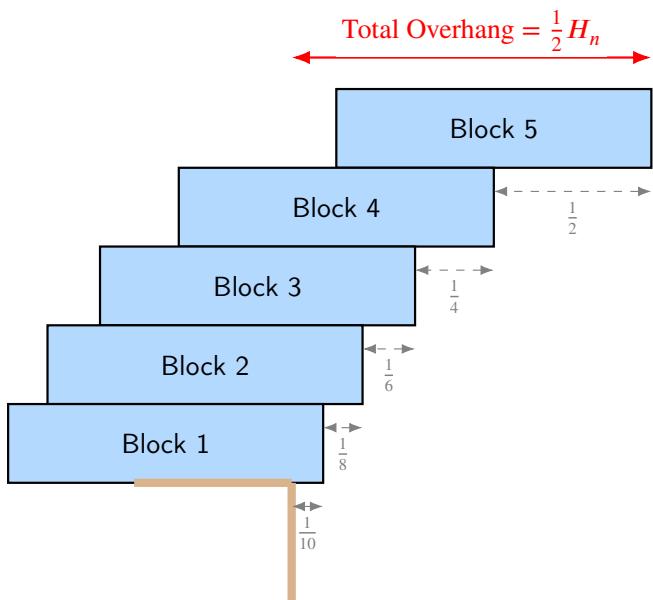
展示 5 块积木优化堆叠实现最大悬臂的图示，公式: Total Overhang = 1/2 H_n。

5 积木堆叠的调和悬臂示意。AlphaEvolve 程序化再发现了此通式。

6) 一个程序化发现的 IMO 方案

AlphaEvolve 用于编写程序解决 2025 年 IMO 某问题 (在 \(n\times n\) 方格中铺砖，使每行每列恰有一个未覆盖单元) 。在平方数 \(n\) 情况下，它通常生成最优砖块数及铺砖构型。结果证明，AlphaEvolve 在竞赛类的构造性问题中也能成功产生目标组合对象的程序。

由 AlphaEvolve 发现的 36x36 网格最优铺砖方案 (2025 IMO 问题之一) 。

一个紧凑的最优铺砖方案实例。

一些速胜与惜败

  • 接触数问题 : 将 11 维空间接触数下界提升至 593；
  • Tammes/Thomson 问题 : 重现多种已知最优球面配置并生成大 \(N\) 的数值候选；
  • 组合集合构造 : 提升和差集与堆积相关常数下界；
  • 挑战失败案例 : 深度分析型或需全新理论技巧的问题暂未突破 (部分仍属“AlphaEvolve-hard”) 。

局限性、问题与最佳实践

AlphaEvolve 强大但非万能，相关实验揭示诸多注意事项:

  1. 验证器设计极其关键 : 低精度或粗糙验证会导致程序钻漏洞。需用高精度或精确算术验证候选。
  2. 数据污染与提示词设计 : 谨防提示泄露解答或过度引导搜索方向。少量专家指引可显著提升性能。具体取舍取决于目标是探索还是优化。
  3. 随机性与多样性权衡 : 强 LLM 提供高质量编辑，廉价模型提供多样性；混合模型往往高效。
  4. 可解释性差异 : 进化启发式可能产生黑箱策略；若解释性重要，宜进化简洁模板或用泛化器模式鼓励简约算法。
  5. 可复现性问题 : 演化过程具有随机性，完全重现难度高；论文与代码库提供种子和验证器以支持重现，但不同运行间结果会有差异。

总结与路线图

AlphaEvolve 展示了将 LLM 与进化程序搜索及严格评估器结合可在大规模上加速数学探索。其关键优势:

  • 将昂贵的 LLM 创造力转化为大量廉价评估；
  • 能发现临时构造与跨输入规模的通用程序；
  • 能整合符号推理与证明系统，实现从模式到形式化定理的流程。

未来重要方向:

  • 更强自动验证与认证 : 更深度集成区间算术、有理算术与验证数值方法；
  • 自动化超参数调整 : 动态适应变异率、种群与模型组合；
  • 增强与证明系统的衔接 : 自动从程序到可由符号系统完善的证明草图；
  • 建立标准化基准 : 构建“AlphaEvolve-hard”问题基准，以描绘可行的数学探索范围。

最终启示

AlphaEvolve 并非取代理解，而是数学探索的新型伙伴——一个能放大人类直觉、启发意外构造、加速发现极值例子的计算探索者。结合人类智慧与 AI 工具 (符号证明器、形式化系统) ，它能将庞大的搜索空间转化为结构化的创造契机。

实践清单: 如何开始使用 AlphaEvolve 式方法

  • 明确验证器定义: 确保评分精准、连续且可收紧；
  • 从搜索模式入手: 当验证便宜时，进化启发式而非单一构造；
  • 采用混合模型策略: 强模型优化 + 弱模型多样性；
  • 在声称结果前用精确/有理数复检；
  • 若需模式或公式，使用泛化器模式并选取有助抽象的输入集。

论文附带代码库中包含代码、提示词、验证器及文中提到的程序化构造。对实践者而言，信息很直接: 配合合适验证器与提示，LLM 引导的程序进化可成为高效的数学探索与构造利器。

致谢 : 本文所述研究源自跨学科团队合作，融合了机器学习工程、数学专业知识与大量计算资源。这些思想与成果是生成模型、优化与形式化数学交汇的前沿研究快照。

延伸阅读

  • 完整论文: 《Mathematical Exploration and Discovery at Scale》 (作者: B. Georgiev, J. Gómez‑Serrano, T. Tao, A. Z. Wagner)
  • 附带问题及代码库 (论文链接中可获取)
  • 相关系统: AlphaProof、Deep Think，以及早期的 FunSearch 和 PatternBoost。

感谢阅读。若你从事构造性或计算数学，值得考虑将 AlphaEvolve 类工具纳入工作流程——它善于生成候选构造与启发式，人类可进一步分析、优化或形式化。