掩码扩散模型 (masked diffusion models) 已成为生成式建模中最强大的框架之一。从复杂推理与语言生成到图像合成和分子设计，这些模型能够迭代地精炼被掩码的数据，以产生连贯且高质量的输出。

然而，尽管前景广阔，掩码扩散模型仍面临一个众所周知的瓶颈: 推理速度慢 。 其迭代解码过程——每一步仅揭示一个或少数几个词元 (token) ——导致数百轮的顺序采样。这极大地限制了它们在需要快速响应生成的现实应用中的使用。

来自 KAIST 的研究论文 “KLASS: KL-Guided Fast Inference in Masked Diffusion Models” 提出了一个简单而优雅的解决方案: KL 自适应稳定性采样 (KL-Adaptive Stability Sampling，KLASS) 。 KLASS 不使用固定的去掩码规则，而是让模型依据自身的置信度与稳定性信号来决定每一步应揭示多少个词元。结果是？采样更快、准确率更高，而且无需额外训练。

在本文中，我们将深入解析 KLASS 的工作机制、其“稳定性”为何重要，以及 KLASS 如何在文本、推理、图像和分子任务中重新定义扩散生成的效率。

快速回顾: 什么是掩码扩散模型？

假设你有一个干净、完整的句子。扩散模型的前向过程会逐步通过将单词替换为特殊的 [MASK] 标记来“污染”句子，直到全部被掩码。模型随后学习反向过程: 一步一步地恢复原始数据。

形式上，时间步 \(t\) 的前向过程可以描述为一个吸收过程，它用掩码索引 \(\mathbf{m}\) 替换词元，由随时间递减的噪声调度 \(\alpha_t\) 控制。

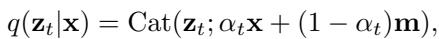
Equation for the forward process in masked diffusion models.

图: 前向过程在噪声调度 \(\alpha_t\) 的控制下，逐步用掩码替换干净词元。反向模型学习从这些掩码序列中预测原始词元。

在推理时，我们从一个完全被掩码的序列开始，迭代地应用学到的反向过程，在祖先采样 (Ancestral Sampling) 的每一步进行采样:

\[ x_{t_{i-1}} \sim p_\theta(x_{t_{i-1}} \mid x_{t_i}) \]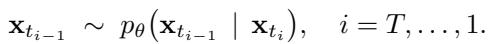

Equation for ancestral sampling in masked diffusion models.

图: 祖先采样反转了掩码扩散过程，在每一步精炼预测，直到所有词元被去掩码。

标准采样器如 Top-1 或 Top-k 是静态的——每步揭示固定数量的词元。即使模型同时对许多词元都很有信心，这些采样器仍只揭示少数几个，从而造成大量顺序计算。

KLASS 改变了这一范式，使去掩码的步伐能够由模型自身动态决定。

核心方法: KL 自适应稳定性采样 (KLASS)

传统方法通常依据预测置信度决定哪些词元应被去掩码。但高置信度并不总意味着正确——模型可能错误地自信。KLASS 引入了第二个、更可靠的信号: 稳定性 , 通过连续预测之间的库尔贝克–莱布勒 (Kullback–Leibler, KL) 散度来衡量。

置信度与稳定性共同提供了判断模型是否值得信任的可靠途径。

两个信号优于一个: 置信度与 KL 分数

KLASS 为时间步 \(t\) 上的每个词元位置 \(i\) 定义了两个简单但互补的指标:

1. 置信度分数 (Confidence Score)

\[ \operatorname{conf}_{t}^{i} = \max_{v \in V} p_t^i(v) \]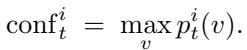

Equation for the confidence score.

图: 置信度分数衡量模型对其每个词元最高预测的偏好强度。

较高的置信度分数表示模型很确定。然而，仅靠置信度可能误导，因为它可能过早地锁定错误词元。

2. KL 分数 (稳定性分数)

\[ d_t^{i} = D_{\mathrm{KL}}(p_t^{i} \parallel p_{t+1}^{i}) \]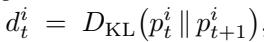

Equation for the KL score.

图: KL 分数跟踪模型在连续步骤间对某个词元的概率分布变化。较低的值代表预测已稳定。

低 KL 分数意味着模型信念几乎未改变——预测变得稳定；高 KL 分数则表明模型仍在犹豫或调整。

研究发现，正确预测的 KL 散度始终显著低于错误预测，如下图所示。

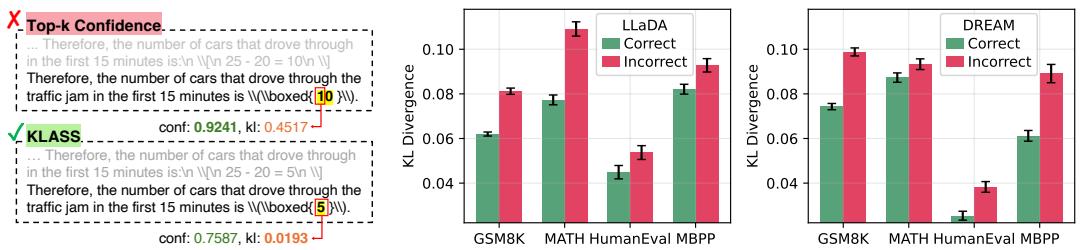
KL divergence as a strong indicator of solution correctness. Part (a) shows KLASS choosing a correct, low-KL token over a high-confidence but incorrect one. Part (b) shows that across benchmarks, correct predictions have lower average KL divergence.

图 1 : KL 散度是正确性的强指标。正确词元的 KL 值远低于错误者，使稳定性成为比原始置信度更可靠的预测信号。

KLASS 算法的实际运作

KLASS 将这两种度量结合为一个动态解码流程。每个时间步 \(t\)，模型检查所有被掩码的词元，判断哪些词元已足够稳定可被去掩码。

一个词元被认为稳定若满足:

  • 置信度超过阈值 \(\tau\)，且
  • 在过去的 \(n\) 步中 KL 散度均低于一个微小阈值 \(\epsilon_{\mathrm{KL}}\)。

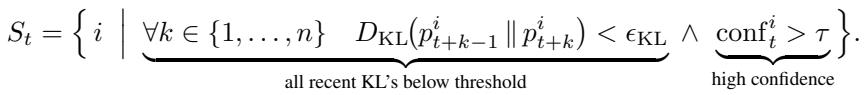
Equation for selecting the set of stable tokens in KLASS.

方程: 稳定词元选择同时检查高置信度与在短历史窗口中的低 KL 一致性。

然后，KLASS 并行地去掩码这个稳定集合 \(S_t\) 中的所有词元:

The KLASS unmasking rule. It unmasks all stable tokens, or falls back to a Top-u strategy if no stable tokens are found.

图: KLASS 的去掩码逻辑。当无词元符合稳定性标准时，算法回退至去掩码 Top‑u 个最自信词元以保证推进。

这一自适应机制让模型能依确定性动态调节速度——预测稳定时揭示更多内容，不确定时则更谨慎。

图 2 展示了这一过程。只有当置信度与稳定性两项均满足时，词元才被揭示。

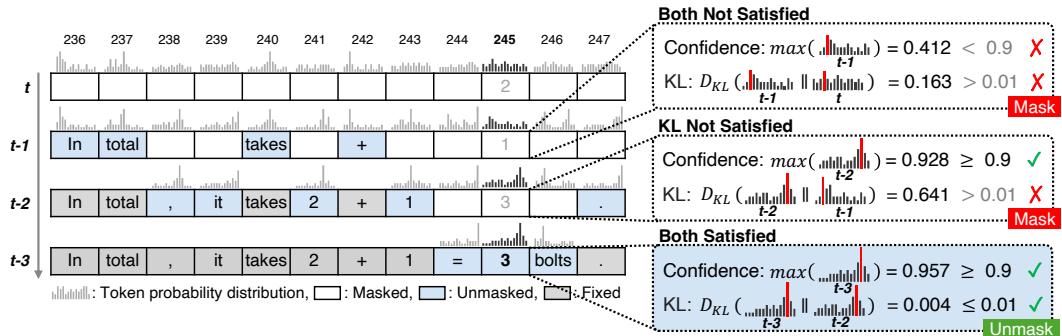
Illustration of parallel decoding with KLASS. Tokens are unmasked only when both high confidence and low KL-divergence criteria are met.

图 2 : KLASS 并行解码。当稳定性与置信度阈值双双满足时，模型可一次性去掩码多个词元，从而在不牺牲准确率的情况下显著提速。

理论洞见: 论文还证明错误词元本质上是不稳定的。随着上下文逐渐正确，其条件分布势必变化，导致更高 KL 散度。因而等待稳定性的策略不仅实用，还具有数学依据。

实验: 检验 KLASS 的表现

KLASS 在推理、文本、图像与分子生成任务上，通过大规模掩码扩散模型进行了评估。

高风险推理: 数学与代码生成

作者在 GSM8K、MATH、HumanEval 和 MBPP 等推理基准上，使用 LLaDA (8B) 与 Dream (7B) 模型测试了 KLASS。

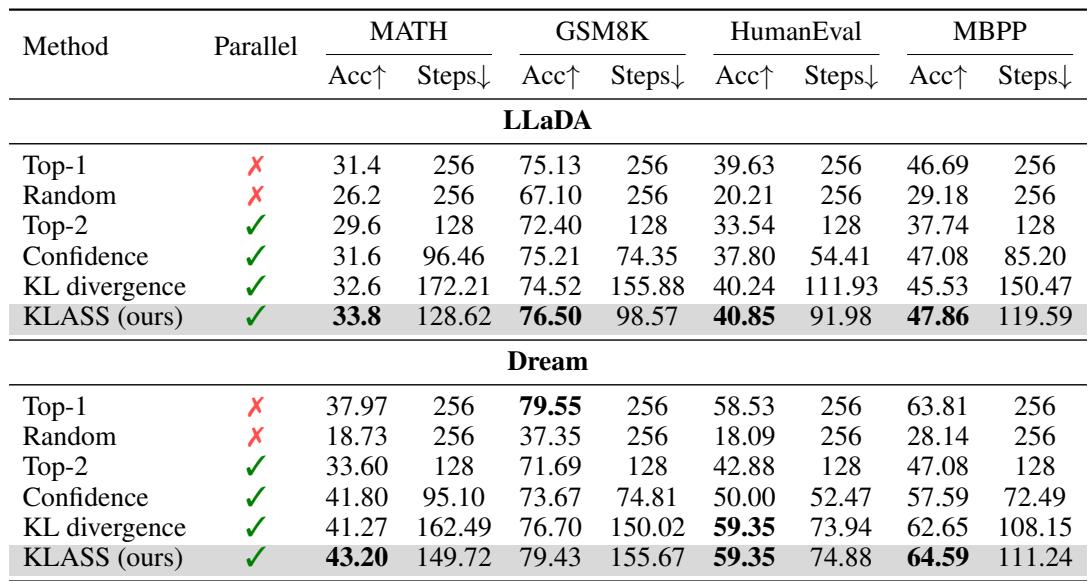
Table 1 shows the performance of KLASS and other samplers on reasoning benchmarks. KLASS achieves higher accuracy with fewer steps.

图/表 1 : KLASS 在推理任务上提升了速度与准确率，超越所有现有扩散采样器。

KLASS 实现了高达 2.78× 的加速，同时准确性亦提高。例如在 GSM8K (LLaDA) 上，步数从 256 降至 98，而准确率从 75.13% 提升至 76.50%。仅依赖置信度或 KL 的方法效果不佳——二者结合才最优。

通用文本生成

KLASS 接着在使用掩码扩散语言模型 (MDLM) 的无条件文本生成中与自回归及扩散基线进行比较。

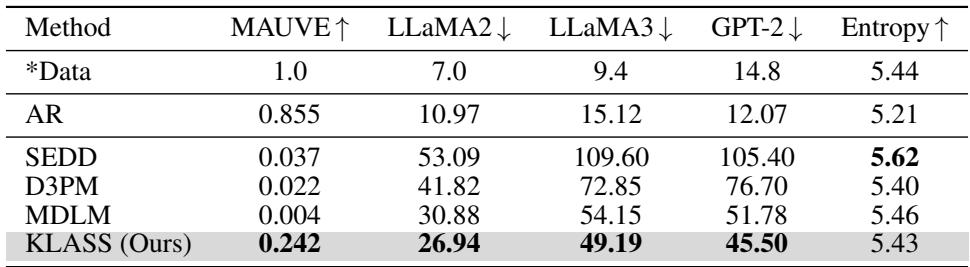
Table 2 shows text generation quality metrics. KLASS achieves higher MAUVE and lower perplexity than other diffusion samplers.

图/表 2 : KLASS 获得更高的 MAUVE 分数 (与真实文本的分布接近度) 及更低的困惑度，生成文本更连贯且流畅。

在多个预言机语言模型 (LLaMA2、LLaMA3、GPT‑2) 上，KLASS 明显降低了困惑度并维持较高熵，使生成文本既多样又自然。

超越文本: 图像与分子

KLASS 展示了其通用性，被进一步应用于图像和分子生成任务。

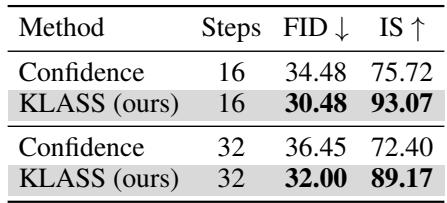
Tables 3 and 4 show that KLASS improves image generation (lower FID, higher IS) and molecular generation (higher reward).

表 3–4 : KLASS 生成的图像保真度更高 (FID 更低、IS 更高) ，分子具有更优目标属性 (更高 QED 与环计数分数) 。

结果表明，KLASS 的自适应机制可无缝拓展至多模态领域，实现扩散推理的通用加速。

这为什么有效？消融研究

消融实验证实, 置信度与 KL 散度阈值缺一不可。

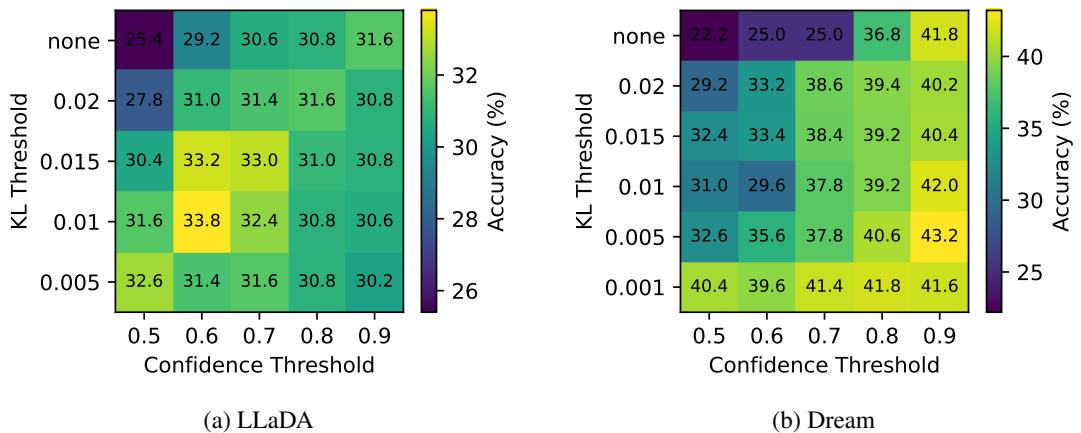
Figure 3 shows heatmaps of accuracy for different KL and confidence thresholds. Adding a KL threshold consistently improves performance.

图 3 : 在置信度过滤的基础上加入 KL 阈值可一致提升准确率，两者相互增强。

另一实验对比了并行与单词元去掩码策略。并行去掩码——一次揭示多个稳定词元——显著减少步数并提高准确率，为剩余预测提供更丰富的上下文。

最后，作者评估了计算开销。尽管 KLASS 设计复杂，其计算量却极低: 计算词元级 KL 分数每步仅增加 1.57% 内存 和 0.21% 延迟 。

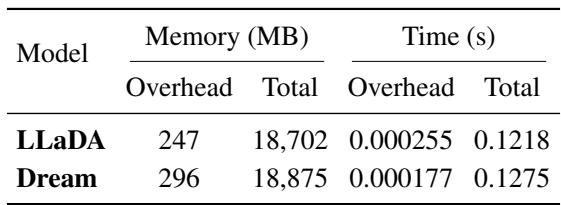
Table 6 shows that the computational and memory overhead of calculating KL divergence is minimal.

表 6 : KL 计算开销可忽略，无需额外的前向传播或复杂操作。

结论: 全新“级别”的采样器

KL 自适应稳定性采样为加速扩散推理提供了一种新思路——倾听模型自身的内部动态。不再仅依靠置信度，KLASS 通过衡量稳定性来判断正确性，把一致性视为更强的可靠信号。

总结:

  • 快速高效: KLASS 可实现高达 2.78× 的加速，同时采样步数减少逾半；
  • 提升准确率: 即使解码更快，性能仍同步提高；
  • 无需训练且通用: 可无需重新训练，直接用于文本、图像与分子生成。

通过结合置信度与 KL 散度稳定性，KLASS 展示了生成模型能够推理自身确定性的可能——从而实现更快、更可靠的预测，为更智能的扩散采样铺平道路。

这不仅是一种更快的算法，更是一种更聪明的算法: 一种根植于学习稳定性的新级别的采样方式。