引言: 空中的噪声

在现代世界中，我们要身处的空气中充满了不可见的数据。从蜂窝网络到军用雷达，电磁信号不断在大气层中穿梭。管理这种混乱的频谱需要自动调制分类 (Automatic Modulation Classification, AMC) 。 这项技术就像是一个数字看门人，负责识别检测到的信号使用了哪种调制方式 (即把数据编码到无线电波上的方法) 。无论是为了动态频谱分配还是监控，系统都必须知道: 这是一个 64QAM 信号吗？或者可能是 QPSK？

深度学习彻底改变了 AMC，用能够直接学习识别信号模式的神经网络取代了死板的特征工程。然而，一个顽固的问题依然存在。当信噪比 (SNR) 下降，或者调制方案看起来极其相似 (例如区分 QPSK 和 8PSK) 时，深度学习模型往往会犹豫不决。它们遭受着预测模糊 (prediction ambiguity) 的困扰。

模型并没有自信地说“这是 A 类”，而是基本上在两边下注，比如给 A 类分配 45% 的概率，给 B 类分配 42% 的概率。这种模糊性扼杀了可靠性。

在这篇文章中，我们将深入探讨最近的一篇论文 《基于模糊正则化的鲁棒自动调制分类》 (Robust Automatic Modulation Classification with Fuzzy Regularization) , 该论文为神经网络中的这种“懒惰”现象提出了一种数学解决方案。研究人员引入了模糊正则化 (Fuzzy Regularization, FR) , 这是一种强迫模型停止含糊其辞，转而学习更清晰、更鲁棒的决策边界的技术。

核心问题: 预测模糊

要理解这个解决方案，我们需要先明白为什么深度学习模型会在这里失效。在理想情况下，分类器会输出一个“独热 (one-hot) ”风格的概率: 正确类别为 99%，其余类别接近 0%。

然而，在信号处理领域，调制类型往往仅在细微的编码位上有所不同，而在噪声环境下，它们的物理波形 (同相和正交分量) 看起来几乎完全相同。

论文作者指出，这导致输出层 (Softmax) 出现了“软”分布。

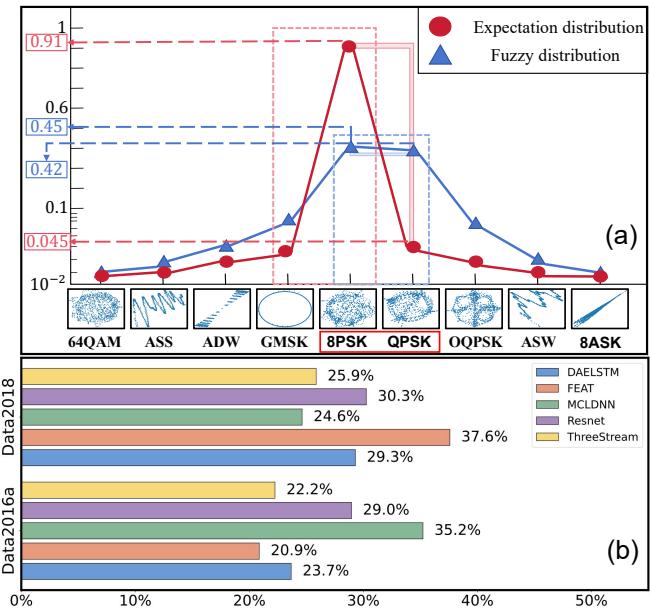
如上图 Figure 1(a) 所示，蓝线代表典型的模糊预测。前两个概率几乎无法区分 (例如 0.45 对比 0.42) 。红线代表我们想要的理想、清晰的预测。

在 Figure 1(b) 中，作者展示了这并非偶然现象。在不同的架构 (ResNet, LSTM 等) 和数据集上，大约 25% 的样本都遭受这种模糊性的困扰。模型并没有学会区分特征；它只是学到了: 比起犯错，模棱两可更安全。

为什么模型会变懒？概率视角的分析

为什么标准的训练 (使用交叉熵损失) 不能解决这个问题？研究人员从数学角度对这一现象进行了建模，以寻找根本原因。

让我们想象一个针对 \(k\) 个样本批次的二分类任务。如果模型感到困惑，某个类别的最高预测概率往往会稳定在一个常数值 \(u\) 附近。

一个批次的标准交叉熵损失计算如下:

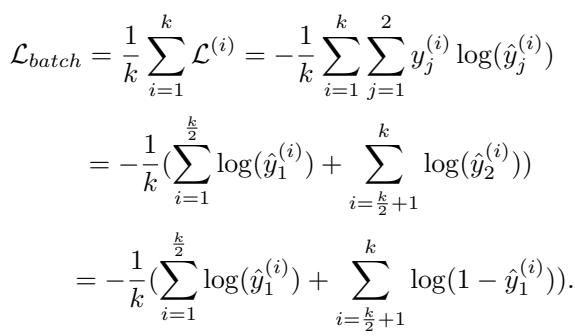
如果我们假设模型难以区分两个类别，分类准确率 \(\alpha\) 本质上就变成了抛硬币 (0.5) 。通过基于误分类概率对期望损失 \(E(\mathcal{L}_{batch})\) 进行建模，研究人员推导出了以下关系:

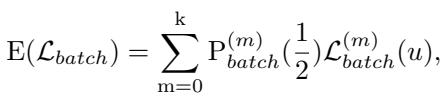
通过进一步推导，他们得出了关于期望损失相对于预测概率 \(u\) 的行为的一个关键见解:

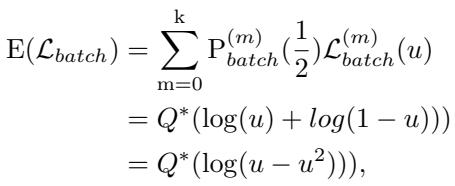
结论是: 数学推导表明，当模型无法找到明显的特征时，期望损失在 \(u = 0.5\) 时达到最小值。用通俗的话说, 当数据很难处理时，损失函数实际上是在奖励模型的模糊行为 。 模型进入了一种“懒惰”状态，通过平滑其预测来控制损失的增长，而不是试图解决区分相似类别的难题。

解决方案: 模糊正则化 (FR)

为了让模型跳出这个懒惰的局部极小值，我们需要惩罚模糊性。我们需要一个正则化 (Regularization) 项——这是添加到损失函数中的额外组件，它相当于在说: “我不只关心你分类是否正确；我还关心你有多确定。”

尝试 1: 熵和方差 (以及它们为何失败)

衡量“无序”或模糊性的最常用方法是熵 (Entropy) 和方差 (L2 范数) 。

• 熵: 高熵意味着高无序度 (模糊) 。
• L2 范数 (方差) : 低方差意味着概率分布得很平坦 (模糊) 。

研究人员考虑基于这些概念定义一个惩罚项 \(M\):

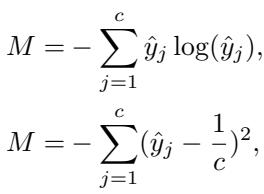
然而，简单地将这些添加到损失函数中会导致训练不稳定。原因在于梯度 。

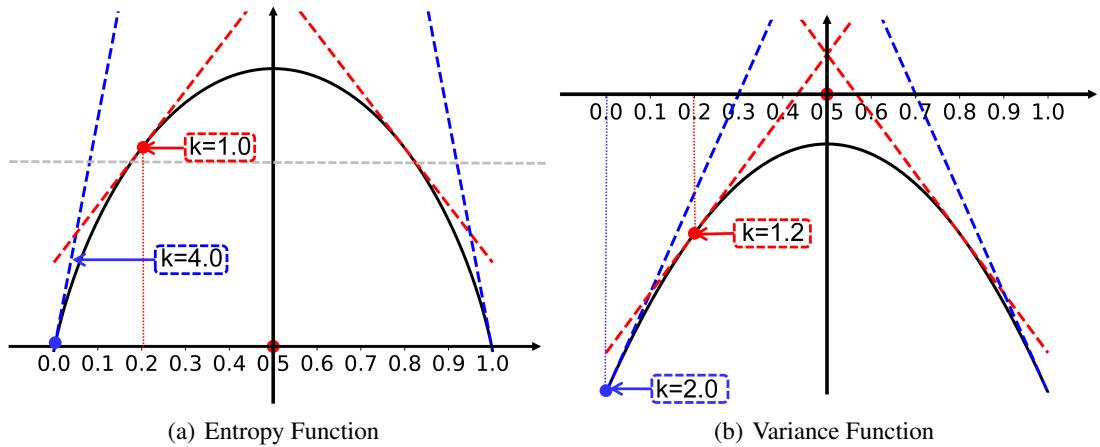
看一看上面的 Figure 7(a) 。 这张图展示了熵函数的梯度 (斜率) 。问题在于，即使预测模糊度很低 (意味着模型变得自信) ，熵函数仍然会返回一个相对较大的梯度更新。这导致模型参数在接近最优解时剧烈震荡，阻碍收敛。

尝试 2: 自适应梯度机制

研究人员意识到他们需要一种“聪明”的惩罚。

1. 高模糊性: 返回大损失和大梯度，强迫模型改变。
2. 低模糊性: 返回小梯度，允许模型稳定地进行微调。

他们设计了一条正则化曲线，其行为类似于函数 \(y = -\log(|x| - 0.5)\)。

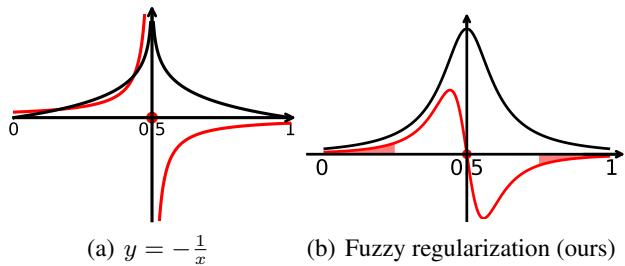
在 Figure 2(b) 中，你可以看到提出的模糊正则化 (FR) 曲线。它在模糊性最高的地方 (0.5) 形成一个“峰值”。随着模型将预测推离模糊的中心 (0.5) 并推向 0 或 1，梯度 (红线) 自然减小，从而稳定训练。

FR 的数学公式

为了实现这一点，作者利用对数正态分布 (Log-Normal Distribution) 函数构建了最终的正则化项。这结合了单个样本的模糊性与整个批次的统计信息。

首先，他们基于 L2 范数定义了单个样本的损失，并对其进行归一化以纯粹关注分布形状:

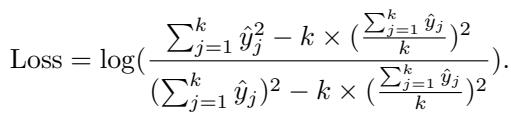
然后，他们将其集成到最终的模糊正则化函数 \(F(\hat{y})\) 中:

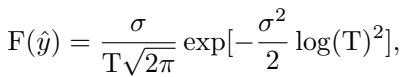
受到以下参数的约束，其中 \(T\) 代表前 \(k\) 个预测类别的方差统计量:

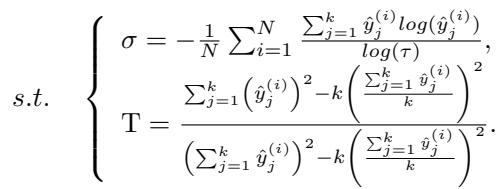
这看起来很复杂，但机制很优雅: 它动态地重新加权样本。 如果一个样本是模糊的，FR 项会激增，主导损失，迫使网络专注于这个“困难”样本。随着样本变得清晰，FR 项消失，让标准的交叉熵损失来处理细节。

实验结果

这套数学理论在现实世界中站得住脚吗？研究人员在三个基准数据集上测试了 FR-AMC: RadioML 2016.10a、2016.10b 和 2018.01A 。 他们将 FR 模块应用于五个不同的最先进模型 (包括 ResNet, LSTM 和 Transformers) ，以证明它无论在哪种架构下都有效。

1. 泛化能力对比

结果是一致的。添加模糊正则化全面提升了性能。

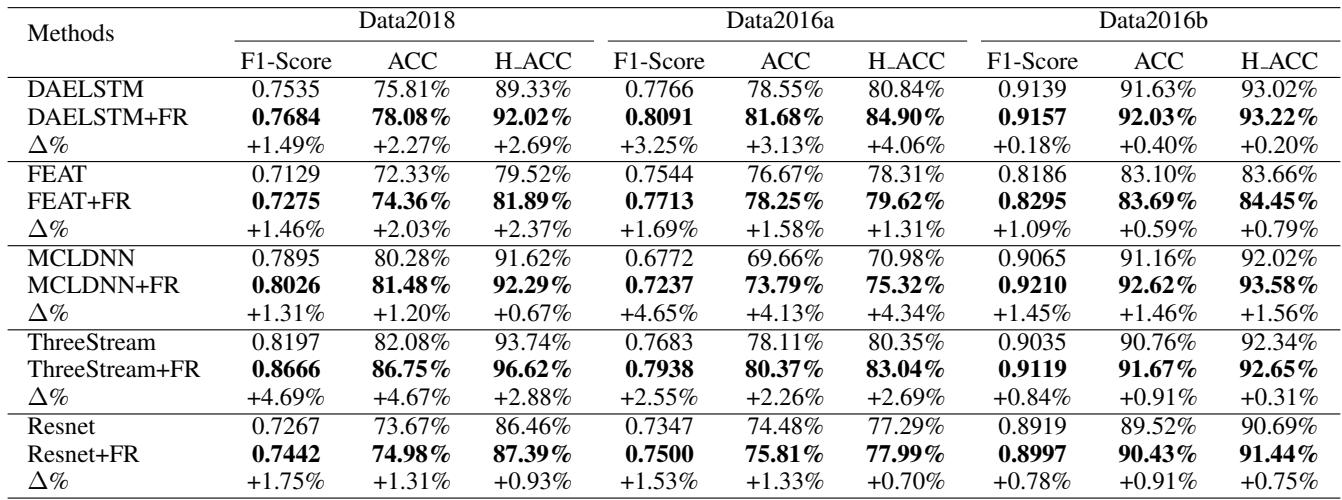
如 Table 2 所示，每一个模型 (DAELSTM, FEAT, MCLDNN 等) 在添加“FR”后，准确率 (ACC) 和 F1-Score 都看到了提升。

• 关键见解: 在预测模糊更常见的“更难”的数据集 (Data2016a) 上，提升最为显著。在 Data2016b 上，基线模型得分已经超过 90%，收益较小但仍为正。这证实了 FR 专门针对“困难”案例。

2. 抗噪鲁棒性

无线电系统的真正考验是噪声。研究人员生成了具有不同噪声因子 (20%, 40%, 60%) 的“噪声”版数据集。

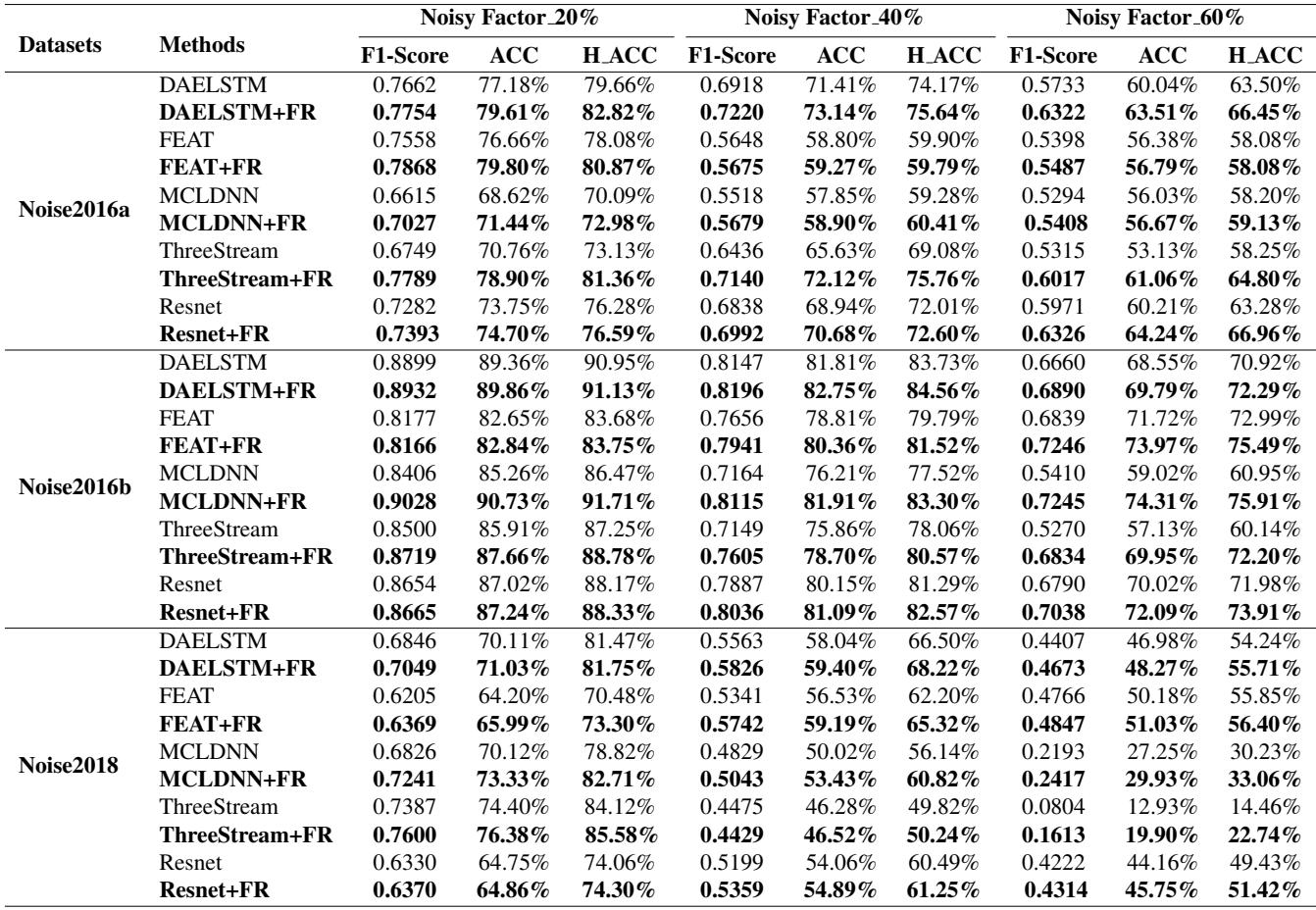
Table 3 显示，随着噪声增加，基线模型和 FR 增强模型之间的差距在拉大。例如，在 60% 噪声的 Noise2016b 上，MCLDNN 模型的准确率仅仅通过添加 FR 就从 59.02% 跃升至 74.31% 。 这表明，通过在训练期间强迫模型减少模糊性，它学到了对干扰更具抵抗力的特征表示。

3. 决策边界可视化

数字固然好，但看到数据聚类效果更佳。研究人员使用 t-SNE 可视化了模型如何区分两种非常相似的调制类型: 8PSK (红色) 和 QPSK (蓝色) 。

在 Figure 3 中，第一行 (无 FR) 显示聚类相互“粘连”，尤其是在噪声增加时。第二行 (有 FR) 显示了更紧密、更清晰的聚类。FR 惩罚有效地迫使模型最大化了这些易混淆类别之间的间隔。

4. 训练速度与稳定性

最后，这种额外的复杂性是否减慢了训练速度？令人惊讶的是，并没有。

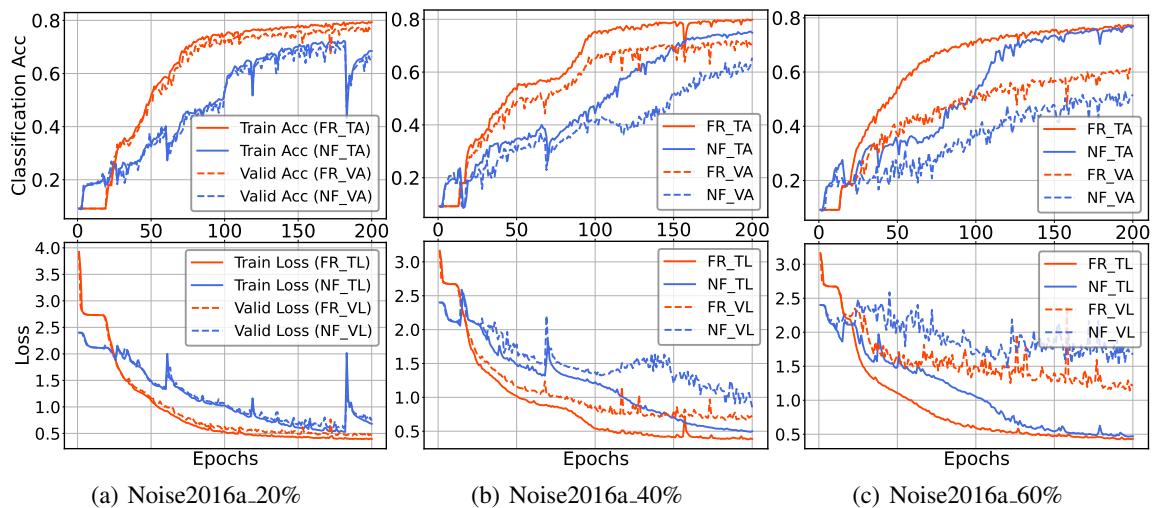
Figure 4 对比了训练曲线。红线 (FR) 比蓝线 (无 FR) 收敛得更快且更平滑。

• 课程学习效应: 通过尽早锐化简单的预测，模型可以不再担心它们，并将梯度更新投入到困难、模糊的样本上。这就像一个自动的“课程”，加速了学习过程。

结论

这篇《基于模糊正则化的鲁棒自动调制分类》论文揭示了我们在训练深度学习模型进行信号处理时一个微妙但严重的缺陷: 倾向于接受模糊性。

通过对这种懒惰进行数学建模，并设计一个具有自适应梯度的模糊正则化项，研究人员提供了一个即插即用的模块，它能够:

1. 惩罚不确定性: 强迫模型做出选择。
2. 稳定训练: 随着信心增长减小梯度。
3. 提升鲁棒性: 显著提高高噪声环境下的性能。

对于 AMC 领域的学生和从业者来说，这是一个宝贵的教训。通往更佳性能的道路并不总是建立更大、更深的神经网络。有时，关键在于损失函数——改变模型学习的方式，而不仅仅是学习的内容。通过拒绝接受“也许”作为答案，FR 推动模型去理解它们所分析信号的真实本质。