在机器学习的世界里，图 (Graphs) 无处不在。从社交网络和化学分子到引用图谱和计算机网络，我们使用图来模拟复杂的关系。在过去的几年里，自监督学习 (SSL) ，特别是图对比学习 (Graph Contrastive Learning, GCL) , 已成为教机器在没有人工标注的情况下理解这些结构的主流方法。

但在现有的范式中存在一个缺陷。

标准的对比学习将图中的每一个节点都视为一个独特的实体。它假设一个节点只与它自己 (或其增强版本) 是“等价”的。这忽略了图的一个基本事实: 等价性 (Equivalence) 。 在计算机网络中，两台不同的服务器可能执行完全相同的角色并连接到类似的设备。在一个分子中，两个碳原子可能在结构上是对称的。对于人类来说，这些节点在功能和形式上是“相同”的。但对于标准的 GCL 模型来说，它们是完全不同的。

在这次深度探索中，我们将研究论文 《Equivalence is All: A Unified View for Self-supervised Graph Learning》 。 作者介绍了 GALE , 这是一个主张我们应该停止将每个节点视为独一无二，并开始根据结构和属性等价性对它们进行分组的框架。

让我们来拆解它是如何工作的，为什么严格的数学定义使其难以实现，以及研究人员是如何通过巧妙的近似方法解决这个问题的。

1. 核心问题: 忽视对称性

要理解为什么 GALE 框架是必要的，我们首先需要看看现有方法缺少什么。

大多数通过对比学习训练的现代图神经网络 (GNN) 都基于一个简单的原则运作: 实例判别 (Instance Discrimination) 。

  1. 获取一个图。
  2. 创建两个略有不同的视图 (例如，通过删除几条边) 。
  3. 教模型识别视图 1 中的节点 A 与视图 2 中的节点 A 是相同的 (正样本对) 。
  4. 教模型识别节点 A 与节点 B、节点 C 以及其他所有节点都是不同的 (负样本对) 。

这对于识别特定节点很有效，但它未能捕捉到语义相似性 。

想象一个社交网络。你有两个用户，Alice 和 Bob。他们互不相识。然而，他们住在同一个城市，做同样的工作，并且都是各自朋友圈的“枢纽”。在结构和功能上，Alice 和 Bob 是等价的。模型应该将他们映射为相似的表示。但标准的对比学习会将他们推开，因为他们仅仅是技术上不同的实例。

这篇论文的作者认为，我们需要将节点等价性显式地纳入学习过程中。

2. 背景: 什么是节点等价性？

在看解决方案之前，我们需要从数学上定义这个问题。论文重点关注两种特定类型的等价性: 自同构等价性 (结构) 和属性等价性 (特征) 。

自同构等价性 (结构)

这是代数图论中的一个概念。如果交换两个节点而不改变图的连通结构，那么这两个节点就是自同构等价的。

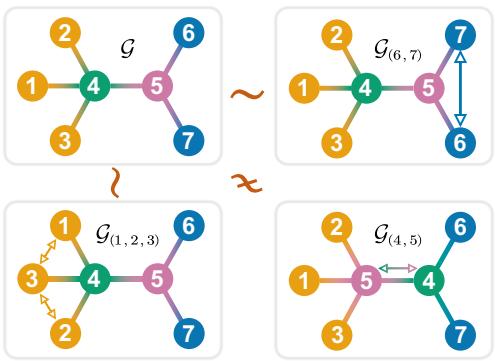
图1. 自同构等价的一个例子。空心双向箭头表示图 G 中的节点置换，以循环表示法显示。

看上面的图 1 。

  • 在左上角的图 (\(\mathcal{G}\)) 中，观察节点 6 和 7。它们都只连接到节点 5。如果你交换节点 6 和节点 7，图看起来完全一样。它们是自同构等价的。
  • 现在看节点 4 和 5。如果你交换它们 (右下角，\(\mathcal{G}_{(4,5)}\)) ，连接关系会发生剧烈变化。节点 5 将连接到 1、2 和 3，而之前并非如此。它们是不等价的。

这种关系的数学定义是:

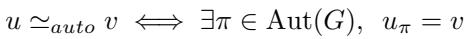
自同构等价性公式

这基本上是说，如果图的自同构群 \(\operatorname{Aut}(G)\) 中存在一个置换 \(\pi\) 将 \(u\) 映射到 \(v\)，则节点 \(u\) 和节点 \(v\) 是等价的。

属性等价性 (特征)

这个更简单。在许多图中，节点拥有特征 (属性) ，如文本、年龄或化学性质。如果两个节点的特征向量完全相同，则它们是属性等价的。

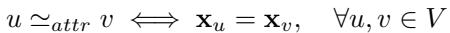
属性等价性公式

为什么这很重要

研究人员分析了几个基准数据集，以此观察这些等价性有多普遍。

表1. 网络和图级数据集中自同构等价节点和图的比例。

如表 1 所示，等价性并非小众的边缘情况。在 MUTAG 和 IMDB-B 数据集中，100% 的图包含自同构等价性。在像 Citeseer 这样的引用网络中，近一半的节点 (46.2%) 拥有结构上的双胞胎。忽视这一点意味着忽视了数据中大量的信号。

3. GALE: 框架

研究人员提出了 GALE (GrAph self-supervised Learning framework with Equivalence，带等价性的图自监督学习框架) 。其目标是学习满足以下条件的节点表示:

  1. 同一等价类中的节点是相似的 (类内) 。
  2. 不同等价类中的节点是不相似的 (类间) 。

架构

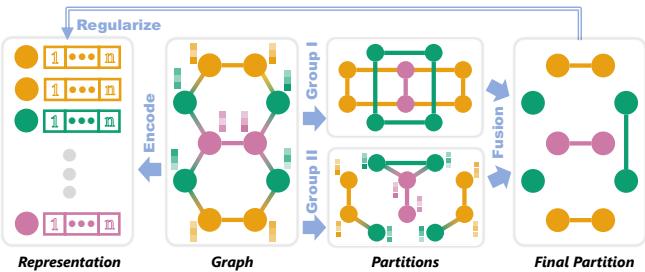
图2. GALE 概览，结合了编码器以及来自结构和基于属性划分的等价约束。

图 2 展示了工作流程:

  1. 输入: 包含结构和特征的原始图。
  2. 划分 (上分支) : 系统分析图以寻找“组”。它计算结构等价性 (Group I) 和属性等价性 (Group II) 。
  3. 编码器 (下分支) : 一个标准的 GNN (如 GCN) 将节点编码为嵌入。
  4. 正则化 (融合) : 划分组作为约束条件。损失函数强制嵌入尊重已识别的组。

融合策略

节点的身份由其在网络中的位置 (结构) 及其固有属性 (属性) 共同定义。为了捕捉这一点，GALE 使用交集 (Intersection) 方法融合了这两个划分。

融合划分公式

这个公式意味着，要使两个节点处于同一个最终的“融合类” (\(F\)) 中，它们必须既是结构等价的 (\(C_i\)) 又是属性等价的 (\(D_j\)) 。这创建了一个精细的、高置信度的分组。

损失函数

一旦定义了组，模型如何学习？作者设计了一个特定的损失函数，分为两部分。

1. 类内损失 (拉近) 这一项关注同一等价类 \(F_i\) 内的每一对节点 \((u, v)\)，并最大化它们嵌入 (\(\mathbf{z}\)) 的相似性。

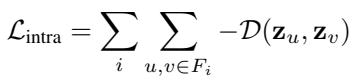
类内损失公式

2. 类间损失 (推远) 这一项关注来自不同类别的节点对，并最小化它们的相似性。

类间损失公式

3. 总等价损失 最终目标仅仅是两者的总和。

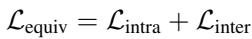
总等价损失公式

4. 工程挑战: 近似

如果你是计算机专业的学生，听到“计算图自同构”时可能会停顿一下。为什么？因为图同构问题以困难著称。在最坏的情况下，精确的自同构检测是 NP难 (NP-hard) 的。在拥有数百万节点的巨型图上运行精确算法 (如 nauty 或 bliss) 在计算上是不可能的。

此外，现实世界的数据是嘈杂的。两个节点可能在属性上几乎相同，但在严格定义下，0.01% 的差异就会将它们分在不同的类中。

为了让 GALE 具有实用性，作者引入了近似等价类 。

用 PageRank 近似结构

作者没有计算精确的轨道，而是使用了 PageRank 。 PageRank 根据节点的结构重要性 (本质上是随机游走者停留在该节点的概率) 为节点分配一个分数。

这种直觉定义在以下关系中:

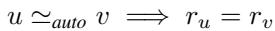
连接自同构和 PageRank 的公式

如果两个节点是自同构等价的 (\(u \simeq_{auto} v\)) ，它们必须拥有相同的 PageRank 分数 (\(r_u = r_v\)) 。

注: 反之并不总是成立 (两个不等价的节点可能拥有相同的分数) ，但这是一个非常强大且计算成本低廉的代理。

PageRank 向量是迭代计算的:

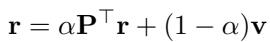
PageRank 计算公式

此操作相对于边数是线性的 \(O(m)\)，这使其比精确的自同构检测快得多。

这种近似真的有效吗？作者使用“信息变异” (Variation of Information, VI) 测试了真实自同构类与 PageRank 类之间的对齐情况，其中 0 表示完美对齐。

表2. 八个基准数据上等价性对齐的信息变异 (VI)。

表 2 显示，在 PubMed 和 Coauthor-CS 等数据集上，对齐几乎是完美的 (VI \(\approx\) 0) 。这种近似捕捉结构对称性的能力几乎与精确 (且缓慢) 的算法一样好。

用距离阈值近似属性

对于节点特征，严格的相等被距离阈值 \(\epsilon\) 所取代。

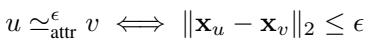
近似属性等价性公式

如果两个特征向量之间的欧几里得距离小于 \(\epsilon\)，则它们被视为等价。这增加了对噪声的鲁棒性。

5. 理论联系

该论文通过等价性的视角，对现有方法进行了精彩的批判。

GALE vs. 图对比学习 (GCL)

作者证明了标准的 GCL 实际上只是 GALE 的一种退化形式 。

在标准的 GCL (如下面的损失所示) 中，模型试图将一个节点与它自己匹配。

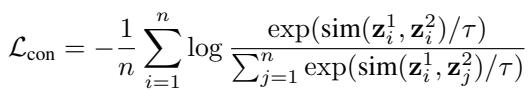
对比损失公式

从 GALE 的角度来看，GCL 假设每个等价类的大小正好为 1。它忽略了图中存在其他等价节点的事实。GALE 通过允许“正样本集”包含恰好等价的不同节点，从而推广了 GCL。

GALE vs. MPNNs 和 Transformers

  • 消息传递神经网络 (MPNNs/GCNs): MPNN 聚合邻居信息。如果两个节点拥有相同的邻域 (等价性) ，MPNN 自然会给它们相似的表示。然而，MPNN 遭受过平滑 (over-smoothing) 的困扰——当你增加层数时，所有节点开始看起来都一样，即使是不等价的节点。

GALE 通过显式强制执行类间损失 (将不等价节点推开) 来解决这个问题。

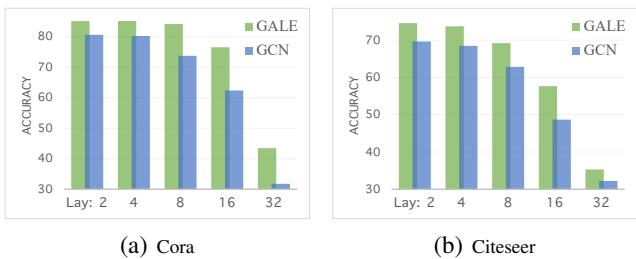
图3. GCN 和 GALE 随深度增加的准确率。

图 3 完美地展示了这一点。随着层数的增加 (x 轴) ，标准 GCN (蓝色) 的准确率由于过平滑而直线下降。GALE (绿色) 即使在 32 层时仍保持高准确率，因为损失函数强制不同的类保持区分。

  • 图 Transformers: 它们依赖位置编码 (PE) 来理解结构。作者发现，大多数流行的 PE 方法 (如拉普拉斯 PE 或随机游走 PE) 不 尊重自同构等价性。

表3. 自同构与基于位置编码的等价性之间的信息变异。

表 3 显示 LapPE 等方法的信息变异很高，这意味着结构上相同的节点经常被分配不同的位置编码，从而混淆了模型。

6. 实验与结果

添加等价约束真的能提高性能吗？作者在图分类和节点分类任务上测试了 GALE。

图分类

这里的目标是对整个图进行分类 (例如，这个分子是否有毒？) 。

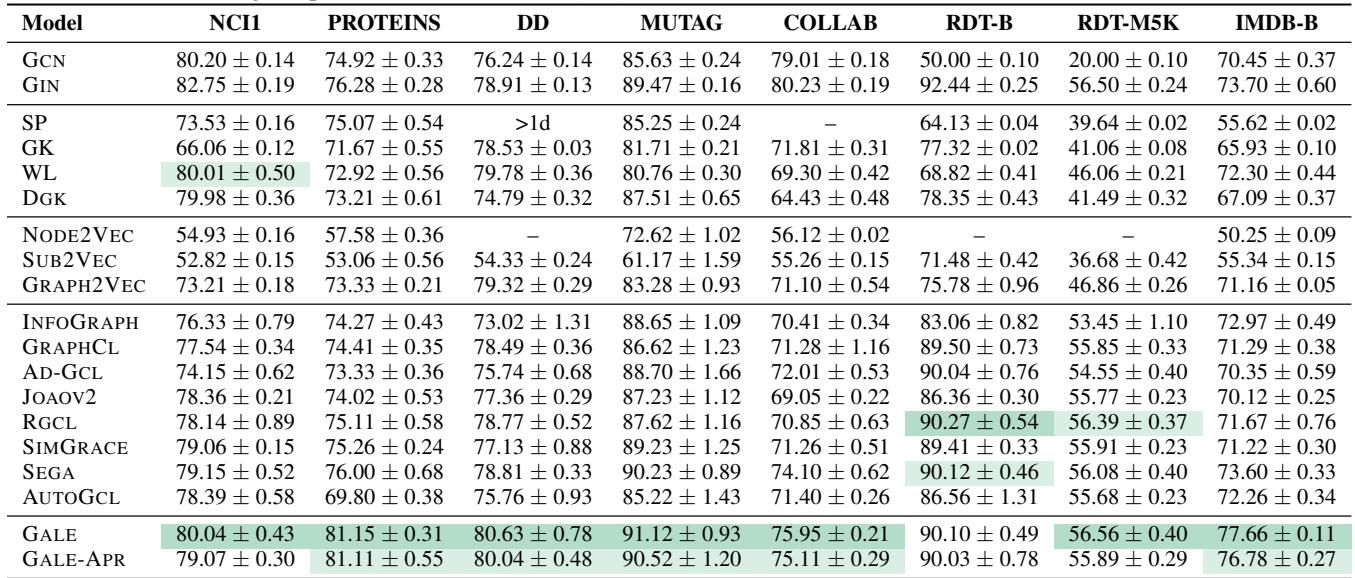
表5. TU 数据集上的监督和无监督分类准确率。

在表 5 中，GALE (及其近似版本 GALE-APR) 始终优于无监督基线 (绿色阴影) ，甚至在几个数据集 (如 IMDB-B) 上击败了像 GIN 这样的监督方法。

节点分类

这里的目标是对特定节点进行分类 (例如，这篇论文在引用网络中的研究主题是什么？) 。

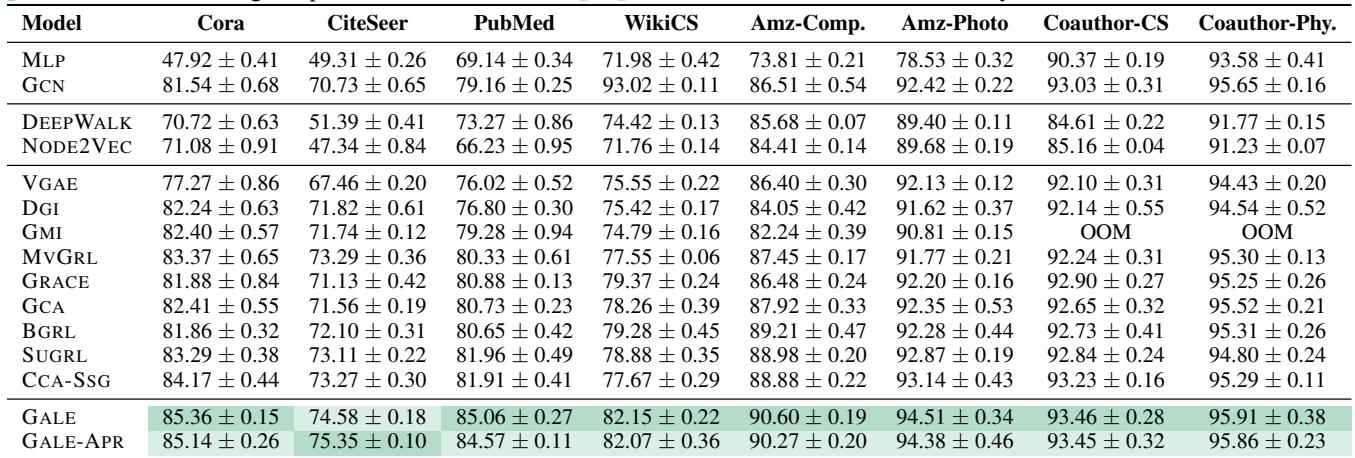
表6. 监督和无监督模型的平均节点分类准确率。

表 6 显示 GALE 在无监督方法中达到了最先进的水平。在 PubMed 数据集上，GALE 达到了 85.06% 的准确率，比之前的最佳方法 (SUGRL) 高出 3% 以上，甚至超过了监督式 GCN 基线 (79.16%) 。

近似的鲁棒性

最后，人们可能会想知道 PageRank 近似是否对阻尼因子 \(\alpha\) (随机游走中传送的概率) 敏感。

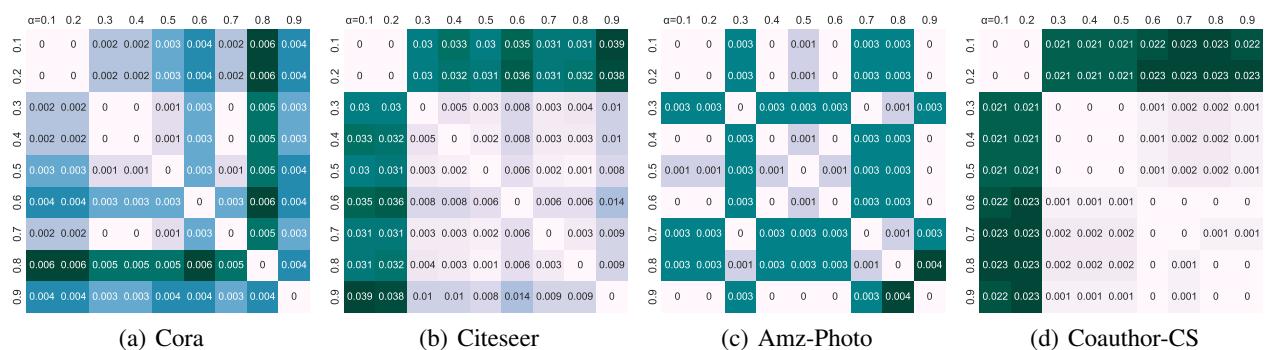
图4. 显示在不同 alpha 值下获得的 PageRank 等价类之间信息变异 (VI) 值的热图。

图 4 展示了比较不同 \(\alpha\) 值生成的划分的热图。极低的值 (主要是深色/黑色) 表明，无论超参数如何选择，生成的等价类都是稳定的。这使得 GALE-APR 在实践中非常可靠。

7. 结论

论文《Equivalence is All》挑战了自监督学习中“实例判别”的习惯。通过认识到图中充满了对称性和冗余，GALE 允许模型学习更丰富、更具语义意义的表示。

关键要点:

  1. 节点并非独一无二: 许多节点在结构或属性上是等价的。
  2. 结合结构与特征: 通过交集进行融合可创建最可靠的等价类。
  3. 近似是关键: 使用 PageRank 和距离阈值使该方法能够扩展到大型现实世界图，而无需进行 NP 难的计算。
  4. 优于对比学习: 通过将“正样本对”的定义从自身增强扩展到等价类，GALE 推广并超越了标准的对比学习。

对于图学习的学生和研究人员来说，GALE 建议转变视角: 与其只问“哪些节点是连接的？”，我们还应该问“哪些节点是可互换的？”