在人工智能快速发展的世界里，研究人员钟爱未解之谜。过去几年中，神经网络中一些违背统计学和学习理论基本定律的奇异行为深深吸引了整个社区。比如模型在严重过拟合之后反而变得更聪明？测试误差先下降，再上升，然后再次下降？这些现象——即所谓的 Grokking (顿悟) 、双重下降 (Double Descent) 和彩票假设 (Lottery Ticket Hypothesis) ——已经催生了成千上万篇试图解释它们的论文。

然而，来自剑桥大学的 Alan Jeffares 和 Mihaela van der Schaar 最近发表的一篇立场论文提出这一个发人深省的问题: 我们试图“解开”这些谜题是在浪费时间吗?

这篇题为《Not All Explanations for Deep Learning Phenomena Are Equally Valuable》 (并非所有对深度学习现象的解释都具有同等价值) 的论文认为，研究社区已经掉进了一个陷阱。通过将这些现象视为需要独特解决方案的孤立谜题，我们往往会制造出“特设 (ad hoc) ”假设，这些假设虽然解释了特定的怪异之处，但对更广泛的领域毫无价值。

在这篇深度文章中，我们将探讨作者对转向社会技术实用主义 (sociotechnical pragmatism) 的呼吁。我们将研究为什么你最感兴趣的深度学习未解之谜在现实世界中可能并不重要，以及如果我们改变视角，它们如何成为解开深度学习基础理论的关键。

现象大观园

在拆解当前的研究方法之前，我们需要了解那些激发了社区想象力的“怪异”行为。作者重点关注了三种挑战我们直觉的特定“边缘案例”现象。

1. 双重下降 (Double Descent)

传统的统计智慧 (偏差-方差权衡) 告诉我们，随着模型变得越来越复杂，它最终会开始过拟合，导致在未见数据上的表现变差。这通常表现为一条 U 型曲线。

然而，研究人员观察到了一些看似不可能的事情: 当你增加参数超过过拟合点后，测试损失有时会再次下降。

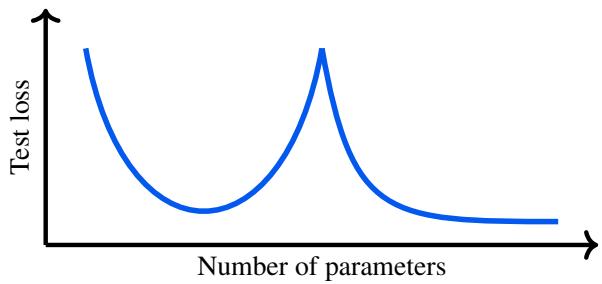
图 1. 双重下降。随着神经网络在参数数量增加的情况下重新训练，其测试损失遵循传统的 U 型曲线，随后出现意想不到的第二次下降。

如图 1 所示，“双重下降”包含一个标准的 U 型曲线，随后是误差的第二次下降。这一观察结果令人震惊，因为它表明大规模的过度参数化 (使模型对于数据来说过于庞大) 实际上是有益的。

2. Grokking (顿悟/突变)

通常，当网络在训练数据上达到 100% 的准确率但在测试集上准确率很低时，我们会停止训练。我们称之为过拟合。

“Grokking”完全颠覆了这一做法。在特定的设置中，如果你在训练准确率达到 100% (且测试准确率持平) 后继续训练很久，模型会突然经历一次“相变”。

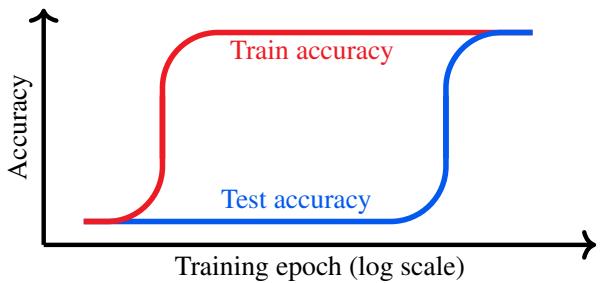
图 2. Grokking。神经网络的训练集准确率在训练早期就达到了 100%，但在测试集上测得的类似泛化性能水平却在很久之后才出现。

图 2 展示了这种延迟泛化。看起来模型是在死记硬背数据 (高训练指标，低测试指标) ，然后奇迹般地，它“领悟 (groks) ”了底层规则，导致测试准确率飙升。

3. 彩票假设 (The Lottery Ticket Hypothesis)

该假设声称，在任何庞大、密集的神经网络中，都存在一个微小的子网络 (一张“中奖彩票”) ，如果从一开始就将其隔离并单独训练，它的表现将达到与完整巨型网络相同的水平。

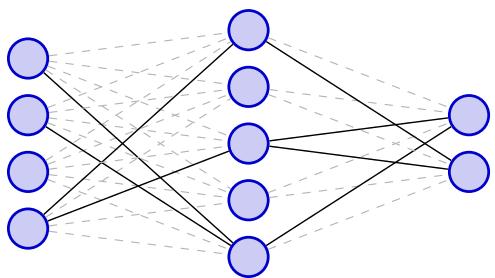
图 3. 彩票假设。一张彩票，即在初始化时就剪除了许多网络参数，在两者都经过训练后，将达到与其密集版本相同的性能。

图 3 将这一概念可视化。这个想法表明，我们庞大模型中的大多数权重都是无关紧要的，实际上只有稀疏的结构在起关键作用。

现实核查: 为什么这些是“边缘案例”

作者在论文早期就抛出了一个残酷的事实: 这些现象在现实应用中极少发生。

如果你正在训练一个大型语言模型 (LLM) 或生产级的计算机视觉系统，你可能永远不会遇到它们。为什么？

  • 在良好实践下双重下降是不可见的: 在现实世界中，我们会使用正则化和早停法 (early stopping) 。我们不会在不调整超参数的情况下盲目增加参数。当你应用最佳正则化等标准技术时，双重下降的凸起就会消失。GPT-4 或 Vision Transformers 等模型的缩放定律通常显示出平滑的改进，而不是锯齿状的双重下降。
  • Grokking 需要人为设置: Grokking 通常在小型算法数据集 (如模算术) 上被观察到。为了让它发生，研究人员通常必须创造人为的条件，例如将权重的初始化设为巨大的数值。在现实场景中寻找“自然” Grokking 的尝试大多失败了。
  • 彩票很难预先找到: 虽然假设是真的——这些子网络确实存在——但在训练完整模型之前找到它们目前是不可能的。你必须先训练巨型模型才能找到那张彩票，这违背了效率的初衷。正如该假设的提出者 Jonathan Frankle 最近承认的那样，在现代硬件上，这可能并不是一条通往实际加速的路径。

如果这些现象对于构建真实 AI 系统的工程师来说不构成实际问题，那我们为什么还要痴迷于它们呢？

作者认为我们把它们当成了谜题。我们看到了一些奇怪的东西，就想“解决”它。但仅仅找到一个符合怪异曲线的数学公式并不等同于做科学研究。

核心方法: 广义理论 vs. 特设假设

这是论文中最关键的概念贡献。要理解为什么当前的研究效率低下，我们必须区分两种类型的解释。

1. 狭隘的特设假设 (Narrow Ad Hoc Hypotheses)

这些是专门为了拟合观察到的现象而设计的解释，除此之外别无他用。它们就像是我们当前理解的一个“补丁”。它们或许能在数学上描述那条曲线，但对其他情况没有预测能力，对构建更好的模型也没有任何效用。

为了展示特设假设的荒谬性，作者基于……素数 (Prime Numbers) , 讽刺性地创建了一个关于双重下降和 Grokking 的“统一理论”。

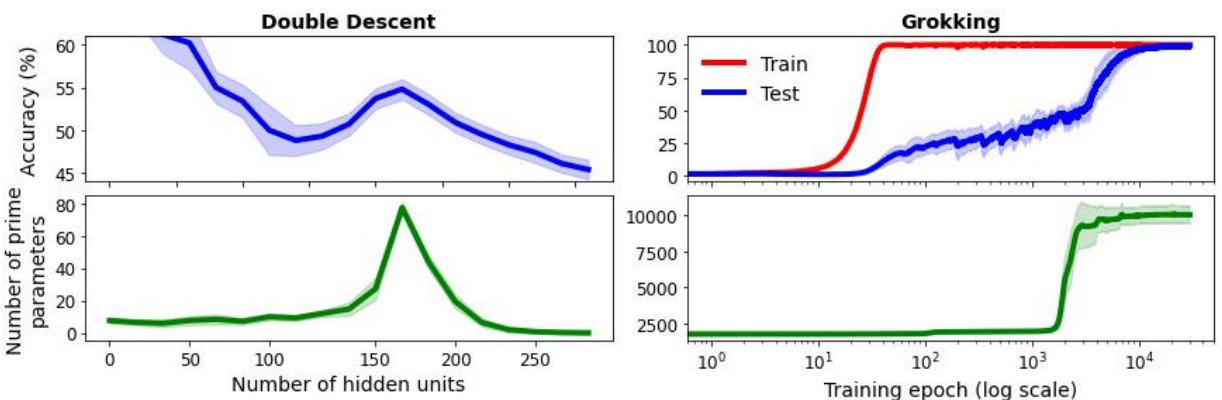
图 4. 基于素数网络参数的双重下降和 Grokking 统一理论。最近文献中的双重下降 (左) 和 grokking (右) 示例通过网络参数中的素数数量 (取整后；底行) 得到了“解释”。在这两种情况下，该指标准确地跟踪了测试性能，在没有访问测试标签的情况下捕捉到了现象的效果。这种夸张的理论恰恰说明了我们所反对的那种狭隘的特设假设。虽然在技术上是正确的，甚至可能引人注目，但这种方法依赖于事后将狭隘的理论拟合到观察到的现象上，极不可能带来具有实际效用的更广泛启示。

仔细看图 4。作者展示了如果你对网络参数进行取整并计算其中有多少是素数，得出的曲线能完美地跟踪双重下降 (左) 和 Grokking (右) 的测试性能。

深度学习的秘密藏在素数里吗? 当然不是。

这是一种相关性伪影 (可能归因于训练期间参数幅度的变化) 。但这说明了一个危险: 你总能找到一个与现象相关的变量。如果你发表一篇论文说“Grokking 是由素数波动引起的”，你就创造了一个狭隘的特设假设 。 对于那个特定的实验，它在技术上是“正确”的，但它是无用的。它没有教给我们任何关于学习动力学、优化或泛化的知识。

2. 广义解释理论 (Broad Explanatory Theories)

相比之下，有价值的解释是利用现象来完善深度学习的一般原则。

我们不应该问: “我们如何修复双重下降？” (它不需要修复；它不在生产环境中发生) 。 我们应该问: “双重下降的存在告诉了我们关于偏差-方差权衡的什么信息？”

价值不在于谜题本身，而在于利用谜题来对我们的基本定律进行压力测试。作者提倡社会技术实用主义 : 即知识的价值取决于其下游效用。

重新评估实验: 寻找效用

如果我们采纳这种实用主义观点，我们要把双重下降和 Grokking 扔进垃圾桶吗？不。作者认为它们是有价值的试验台 , 前提是我们停止试图“解决”它们，开始利用它们来更新我们的心智模型。

以下是作者建议我们如何重新构建关于这三个主题的研究:

重新思考双重下降

  • 错误的方法: 试图在真空中对第二次下降的峰值进行数学建模。
  • 实用主义方法: 用它来挑战经典的偏差-方差权衡。这一现象证明了“过拟合”不是一个简单的二元状态。它引导发现了良性过拟合 (benign overfitting) ——即深度模型可以记忆噪声但仍能良好泛化的观点。这是一个巨大的、可泛化的洞见，它改变了我们在每个领域思考模型容量的方式，而不仅仅是在出现双重下降的边缘案例中。

重新思考 Grokking

  • 错误的方法: 发明复杂的理由来解释为什么模型在 10,000 个 epoch 后突然学会了模算术。
  • 实用主义方法: 利用 Grokking 来研究进度度量 (progress measures) 。 Grokking 告诉我们，“训练准确率”和“测试准确率”是理解模型内部状态的糟糕指标。模型在平台期确实在学习——我们只是没有测量正确的东西。这种认识推动了对“特征学习”与“惰性学习”的研究，帮助我们开发更好的指标来监控真实模型的训练健康状况。

重新思考彩票

  • 错误的方法: 试图构建算法在初始化时寻找彩票 (这在很大程度上已经失败了) 。
  • 实用主义方法: 利用该假设来理解稀疏性 (sparsity) 。 即使我们不能尽早找到彩票，它们存在的事实证明了模型极其低效。这一理论支持为量化 (quantization) (使权重变小) 和参数高效微调 (PEFT) 等实际进步提供了支撑，这对于今天在消费级硬件上运行 LLM 至关重要。

未来研究指南

作者总结道，我们需要让研究变得更科学，而不是像排行榜竞赛。在机器学习的许多领域，目标是“最先进水平” (SOTA) 。但在研究现象时，SOTA 并不适用。你不是在试图击败基准；你是在试图揭示真相。

为了引导研究人员远离“素数理论”并走向有用的科学，作者提出了一个自我评估清单。

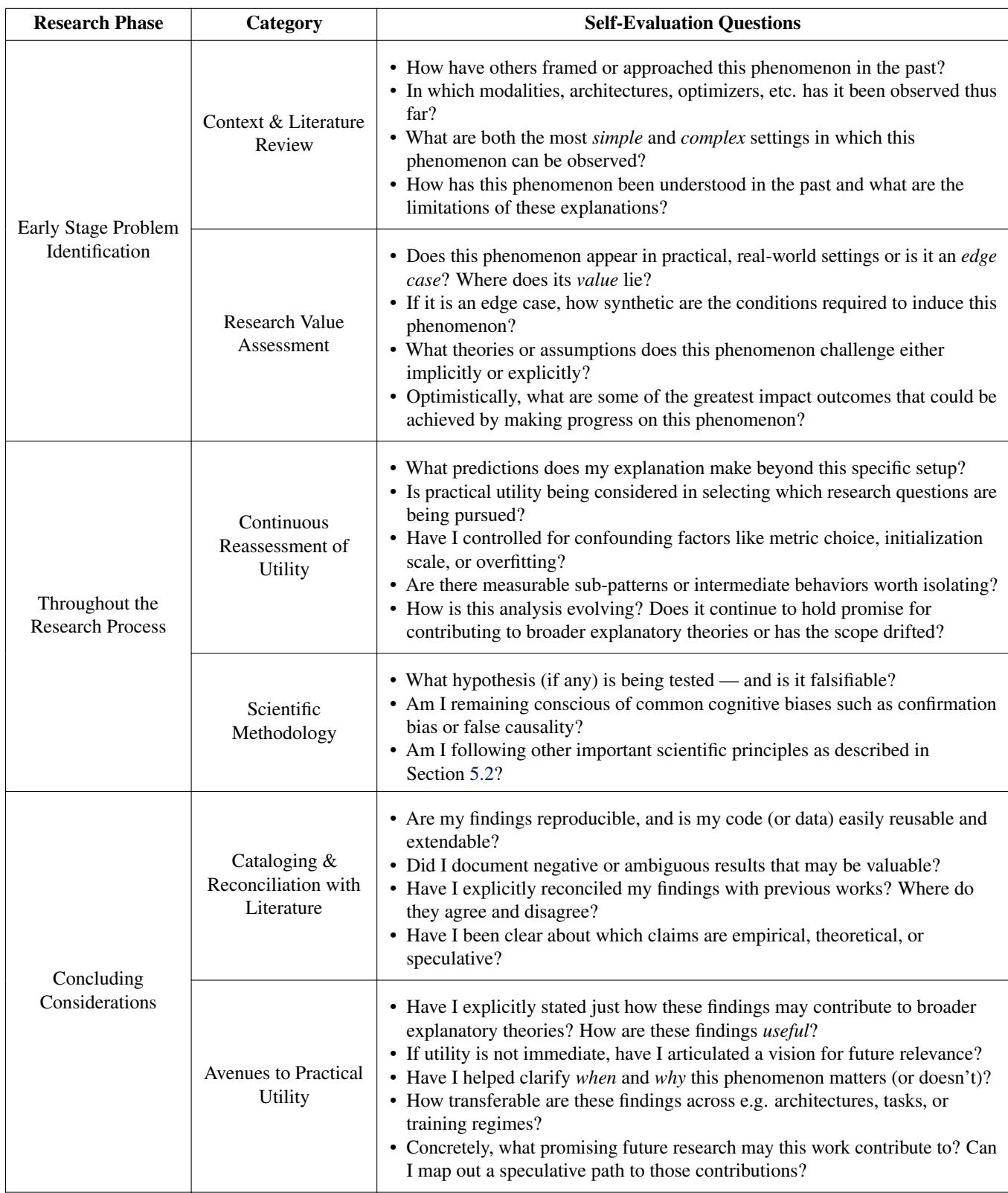
表 1. 自我评估清单。一组供研究人员在研究深度学习现象的每个阶段考虑的关键问题。虽然可能没有严格的“正确”答案，但考虑这些点可能有助于将研究与本工作的立场保持一致。

这份清单 (表 1) 迫使研究人员停下来问一些难题:

  1. 这是一个边缘案例吗? 诚实一点。这会发生在 ChatGPT 中，还是只发生在设置怪异的 MNIST 上？
  2. 我的解释能预测其他事情吗? 如果你的理论只能解释你那张特定的图表，那就是特设的。
  3. 它是可证伪的吗? 你能设计一个实验来证明你是错的吗？

深度学习的“科学方法”

论文主张回归经典的科学原则:

  • 预注册 (Preregistration) : 在运行实验之前陈述你的假设，以防止事后将理论拟合到数据上。
  • 编目 (Cataloging) : 社区应该建立这些现象的高质量、开放的代码库，而不是每个人都重新发现相同的怪异行为。
  • 协作 (Collaboration) : 从竞争性的寻找解释转向集体性的理论构建。

结论: 从谜题到进步

深度学习正在成熟。我们正在通过那个把东西扔进锅里并对冒出的奇怪烟雾感到惊奇的“炼金术”阶段。

Jeffares 和 van der Schaar 的工作是一次至关重要的干预。他们提醒我们，虽然像 Grokking 和双重下降这样的现象令人着迷，但它们不是最终目标。我们必须抵制像解谜者那样行事的冲动，仅仅因为拼图拼凑在一起就感到满足。

相反，我们必须像科学家一样行事。我们应该将这些异常视为压力测试——这是打破我们要现有理论并建立更稳健、更普遍定律的机会，这些定律实际上能帮助我们在现实世界中部署可靠的 AI。

下次当你看到一篇声称“解开”深度学习谜题的论文时，问问你自己: 这是一个广义解释理论，还是仅仅在数素数?