解锁因果秘密: 如何高效列举含有隐变量的图

在人工智能和因果推断的世界里，我们要处理的往往是不完整的图景。我们可以观测到数据——比如病人的症状或国家的经济指标——但我们很少能看到驱动这些观测结果的完整机制。几乎总会有“隐变量” (latent variables) 存在，即那些影响我们所见但未被记录的隐藏因素。

当我们试图在存在这些隐藏因素的情况下绘制因果关系图时，我们得到的不是一张单一、清晰的地图，而是一“类”可能的地图。在这个类中导航以找到每一个具体、有效的因果解释是一个巨大的计算难题。

今天，我们将深入探讨一篇最近的研究论文，该论文解决了这一领域的一个关键瓶颈。我们将探索 MAGLIST-POLY , 这是一种能够以 多项式延迟 (polynomial delay) 列举所有可能的因果图 (具体来说是最大祖先图，即 MAGs) 的算法。这是相对于以前指数级时间方法的一个重大飞跃，使研究人员能够更快地探索因果可能性。

因果图的全貌

为了理解这个解决方案，我们首先需要理解问题所在。让我们来分解一下因果图的层级结构。

从 DAG 到 PAG

在理想世界中，如果我们测量了每一个相关变量，我们可以用 有向无环图 (Directed Acyclic Graph, DAG) 来表示因果关系。在 DAG 中，从 \(A \rightarrow B\) 的箭头意味着 \(A\) 导致 \(B\)。

然而，在现实世界中，我们面临着 隐混淆因子 (latent confounders) (隐藏的共同原因) 和 选择偏差 (selection bias) (影响数据收集的未记录因素) 。当这些因素存在时，仅仅依靠观测变量的简单 DAG 是不够的。我们使用 最大祖先图 (Maximal Ancestral Graph, MAG) 来表示我们 可以 看到的变量之间的因果关系，同时隐式地考虑到我们 无法 看到的变量。

问题在于: 多个不同的 MAG 可能会在数据中产生完全相同的统计模式。这组在统计上无法区分的 MAG 被称为 马尔可夫等价类 (Markov Equivalence Class, MEC) 。

由于我们无法仅凭观测数据区分这些 MAG，我们将整个类总结为一个单一的对象，称为 偏祖先图 (Partial Ancestral Graph, PAG) 。

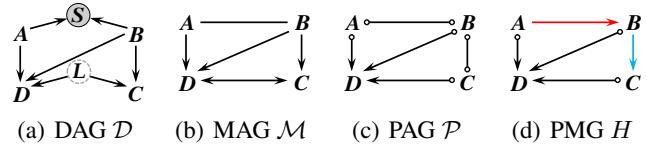
图 1 展示了这种层级结构:

• (a) DAG: 包含隐变量 \(L\) 和 \(S\) 的基本事实 (Ground truth) 。
• (b) MAG: 描述 观测 变量 (\(A, B, C, D\)) 之间因果关系的表示。
• (c) PAG: 我们实际从数据中学到的东西。注意那些圆圈 (\(\circ\)) 。这些代表不确定性。一条边 \(A \circ\!\to B\) 意味着“我们知道存在某种连接，且 \(B\) 不是 \(A\) 的祖先，但我们不知道是 \(A\) 导致 \(B\)，还是存在隐藏的混淆因子。”

问题: 列举可能性

PAG (图 1c) 很有用，但它很模糊。对于许多下游任务——比如估计药物的因果效应，或设计最有效的实验来区分不同的假设——我们需要查看具体的底层 MAG。

我们需要一种方法来获取一个 PAG，并指出: “这就是这个摘要中可能存在的所有具体 MAG 的列表。” 这个过程称为 MAG 列举 (MAG Listing) 。

计算瓶颈

列举 MAG 比列举 DAG 要难得多，因为 MAG 有更多类型的边 (有向 \(\to\)、双向 \(\leftrightarrow\) 和无向 \(-\)) 。

之前最先进的方法，称为 MAGLIST，使用了一种递归方法。它会选择一个节点 (变量) ，并尝试同时解决与它相连的 所有 不确定边。虽然有效，但这种方法有一个主要缺陷: 指数级延迟 (Exponential Delay) 。

延迟是指算法在找到前一个图后，输出 下一个 有效图所需的时间。由于 MAGLIST 试图一次性枚举围绕节点的所有边组合 (即“局部结构”) ，其复杂性随着邻居数量呈指数级增长 (\(2^d\)) 。

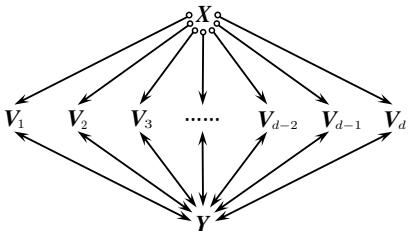
如 图 7 所示，如果一个节点 \(X\) 连接到许多其他节点 (\(V_1\) 到 \(V_d\)) ，试图一次性解决所有这些圆圈会产生巨大的可能性扇出 (fan-out) ，从而拖慢系统。

解决方案: MAGLIST-POLY

这篇论文背后的研究人员提出了一种改进的方法: MAGLIST-POLY 。 其目标是实现 多项式延迟 , 这意味着找到下一个图的时间随图的大小进行可控的缩放，而不是指数级增长。

策略: 单例背景知识 (Singleton Background Knowledge)

核心洞察简单而强大。与其试图同时猜测与节点相连的 所有 边的方向，不如 逐一 猜测？

这个概念依赖于 背景知识 (Background Knowledge, BK) 。 BK 是我们假设为真的外部信息 (比如“我们知道 A 导致 B”) 。

• 局部 BK (Local BK) : 猜测围绕一个节点的所有边 (旧的 MAGLIST 使用的方法) 。
• 单例 BK (Singleton BK) : 仅猜测 一条 特定边或圆圈的方向。

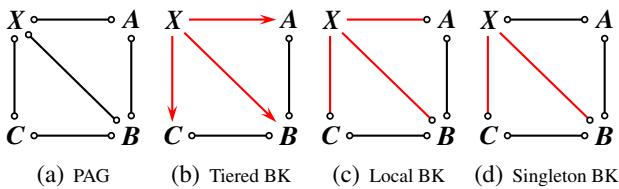
图 3 可视化了这种差异。

• (c) 局部 BK: 我们定义了 \(X\) 与其 所有 邻居 (\(A, B, C\)) 之间的关系。
• (d) 单例 BK: 我们仅定义了 \(X\) 与 一个 邻居 (\(B\)) 之间的关系。

通过引入 单例 BK , 算法避免了指数级爆炸。它做一个小的选择，传播该选择的影响，然后继续。

挑战: “局部完备性” (Local Completeness)

你可能会问，“如果逐一处理更快，为什么我们不一直这样做呢？”

做微小的、增量式选择的危险在于，你可能会把自己逼进死胡同。你可能会以某种局部看起来没问题的方式定向一条边 \(A \to B\)，但这暗示了五步之后会出现你目前还看不到的矛盾。如果你不立即意识到这一点，你就会浪费时间探索搜索树的无效分支。

为了使单例 BK 发挥作用，我们需要 定向规则 (Orientation Rules) 。 这些是逻辑规则，比如“如果 \(A \to B\) 且 \(B \to C\)，你必须将 \(A\) 和 \(C\) 之间的边定向为……”

为了保证多项式延迟，定向规则必须是 局部完备的 (Locally Complete) 。 这意味着在我们做出猜测 (单例 BK) 后，规则必须立即识别出该节点处 所有 被强制为某种方式的其他边。如果规则遗漏了某些东西，算法可能会输出无效的图或卡住。

新颖的定向规则

作者发现现有的定向规则对于单例 BK 来说是不够的。他们确定了旧规则未能触发必要定向的场景。

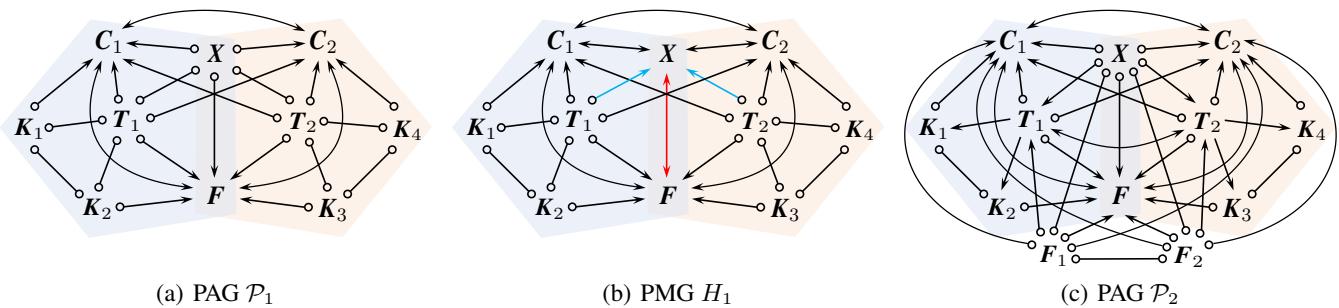
图 4 展示了为什么需要新规则。在 (a) 中，如果我们引入知识: \(C_1\) 导致 \(X\) 且 \(X\) 导致 \(C_2\)，逻辑上 必须 存在一条边 \(X \to F\)。然而，现有规则 (如 \(\mathcal{R}_{12}\)) 无法捕捉到这一点，导致 (b) 中所示的矛盾，即形成了一个无效的未屏蔽对撞 (unshielded collider) 。

为了解决这个问题，作者提出了三条新规则: \(\mathcal{R}_{14}\)、\(\mathcal{R}_{15}\) 和 \(\mathcal{R}_{16}\)。

这些规则的一个关键概念是确定一个节点相对于中心节点 \(X\) 是否 “先于” (prior to) 另一个节点。

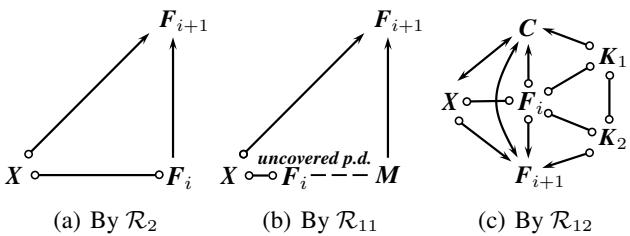
图 5 说明了这个“先于”的概念。它本质上是在检查影响链。如果 \(F_{i+1}\) 导致 \(X\)，这是否会通过像 \(\mathcal{R}_2\) 或 \(\mathcal{R}_{11}\) 这样的规则强制 \(F_i\) 也导致 \(X\)？通过将其形式化，新规则可以检测到以前的规则集遗漏的必要定向。

算法实战

有了新的逻辑, MAGLIST-POLY 使用两个嵌套循环来运行:

1. 外层循环: 选择一个仍有不确定边 (圆圈) 的顶点 \(X\)。
2. 内层循环: 逐一 枚举 \(X\) 处的圆圈。

• 它猜测一个方向 (例如，\(X \to A\)) 。
• 它应用 局部完备定向规则 来更新图。
• 它递归处理 \(X\) 处的下一个圆圈。

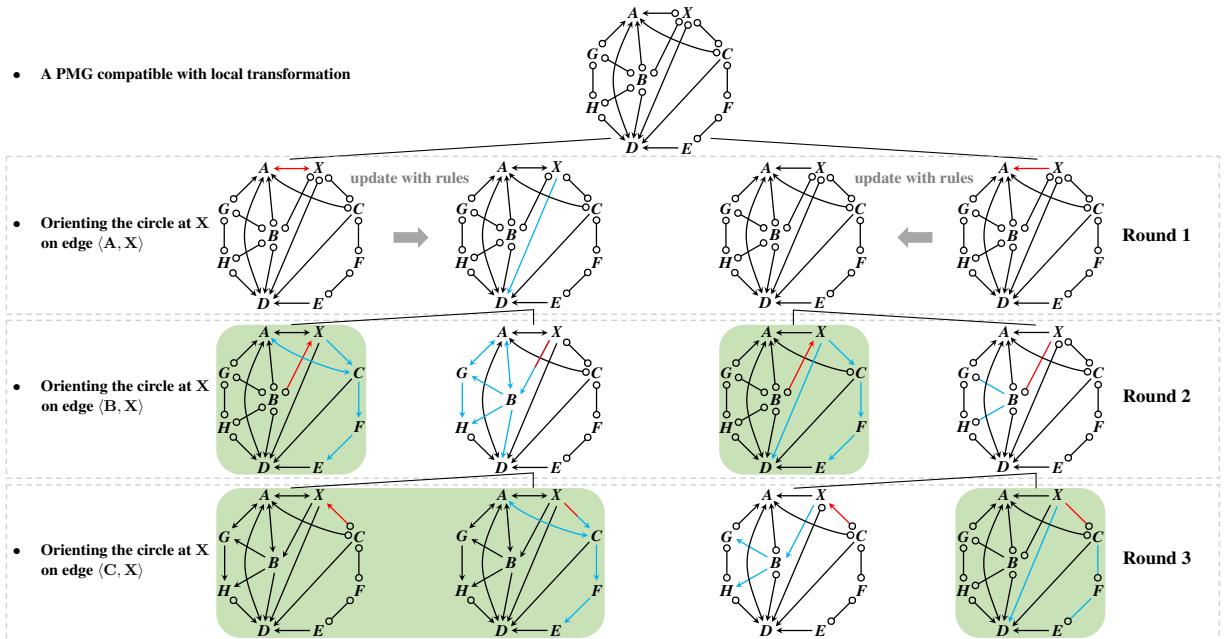
图 6 可视化了这个内层循环。

• 第 1 轮: 我们关注 \(X\) 和 \(A\) 之间的边。我们做一个猜测 (红色箭头) 。我们应用规则 (蓝色箭头) 来更新图的其余部分。
• 第 2 轮: 我们移动到 \(X\) 和 \(B\) 之间的边，猜测并更新。
• 第 3 轮: 我们移动到 \(X\) 和 \(C\)。

注意带阴影的图。这些代表了 \(X\) 处所有圆圈都已解决的有效状态。这些状态被传回外层循环。

方法对比

将此与以前的方法进行对比很有帮助。

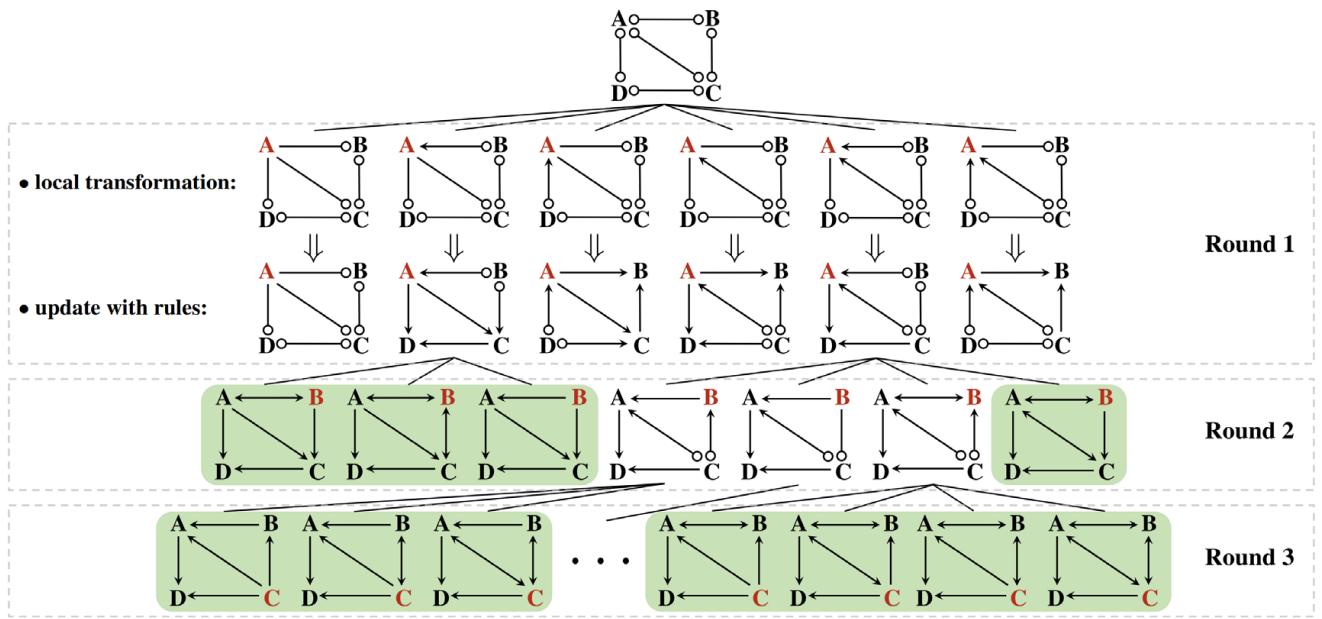
在 图 10 (旧方法) 中，算法获取一个图并生成节点 A 的 所有 有效局部结构，然后是节点 B，依此类推。它在每一步都做“繁重的工作”。相比之下，新方法 (图 6) 采取更小、更轻量的步骤，确保发现有效图之间的时间保持简短。

实验结果: 多项式 vs. 指数级

这种理论上的改进在实践中有意义吗？实验结果给出了响亮的肯定。

作者将 MAGLIST-POLY 与旧的 MAGLIST 以及基线 BRUTE-FORCE (暴力求解) 方法进行了比较。他们测量了随着图的大小 (\(d\)) 和密度 (\(\rho\)) 增加，列举 MAG 所需的时间。

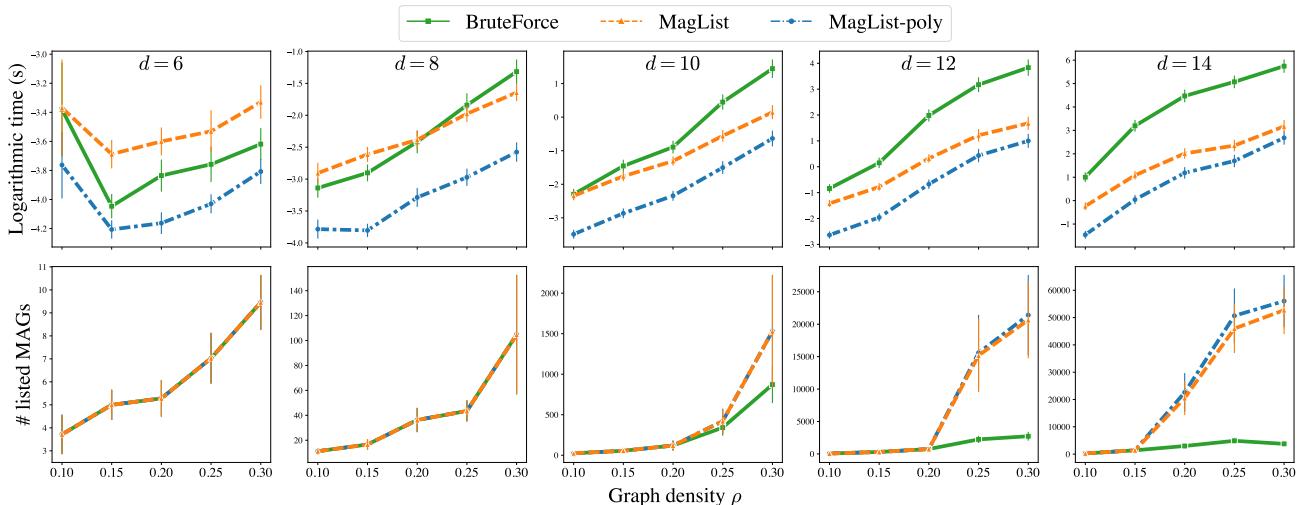
图 9 说明了一切。看第一行 (对数时间) :

• 绿线 (Brute Force) : 立即爆炸。
• 橙线 (MagList) : 表现尚可，但在特定密度下会出现峰值。
• 蓝线 (MagList-Poly) : 赢家。即使图的大小 (\(d\)) 增加到 14 个节点，运行时间仍显着低于其他方法且更稳定。

这证实了避免 \(2^d\) 枚举使得该算法能够高效处理更大、更密集的因果图。

关于完备性的注记

论文最后提出了一个迷人的理论观察。虽然提出的规则是 局部 完备的 (足以让算法工作) ，但它们对于一般的背景知识并非 全局完备 。

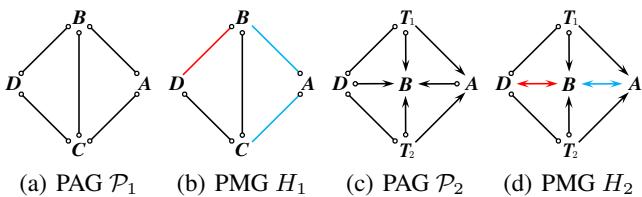
图 8 提供了反例。在 (b) 中，知道 \(D \to B\) 逻辑上暗示了 \(C - A\)，但即使是新规则 (\(\mathcal{R}_{14}-\mathcal{R}_{16}\)) 也无法推导出这一点。这凸显了虽然我们解决了多项式延迟问题，但寻找适用于 所有 因果推断场景的完美规则集仍然是一个未解决的数学挑战。

结语

MAGLIST-POLY 代表了因果发现领域向前迈出的关键一步。通过将列举因果图的复杂问题分解为更小的、单边的决策——并用强大的新逻辑规则支持这些决策——我们现在可以更快地探索隐变量模型的空间。

对于学生和研究人员来说，这意味着因果实验设计和效应估计的工具将变得更具可扩展性，使我们能够处理生物学、经济学等领域中更大、更复杂的系统。

主要收获

• PAGs 代表了一类含有隐变量的可能因果图。列举这些图对于分析至关重要。
• 以前的方法因为试图一次性解决局部结构而遭遇 指数级延迟 。
• MAGLIST-POLY 通过使用 单例背景知识 (Singleton Background Knowledge) (一次定向一条边) 实现了 多项式延迟 。
• 这种方法需要新的 局部完备定向规则 (Locally Complete Orientation Rules) 来确保有效性，而无需穷举搜索。
• 虽然高效，但针对所有场景寻找真正完备的定向规则集的工作仍在继续。