引言

图神经网络 (GNNs) 彻底改变了我们处理数据的方式。从预测蛋白质结构到在社交媒体上推荐新朋友，GNN 在利用数据点之间的连接方面表现出色。但这里存在一个显而易见却常被忽视的巨大障碍: 隐私 。

现实世界的图——如社交网络或金融交易网络——通常充满了敏感的个人信息。我们希望利用这些数据训练模型来解决有用的问题，但我们不能牺牲构成这些图的个人的隐私。

目前隐私保护的黄金标准是本地差分隐私 (Local Differential Privacy, LDP) 。 在 LDP 设置中，用户在数据离开设备之前，会自己向数据中添加噪声。服务器只能看到加噪后的版本。虽然这对隐私保护非常有利，但对效用 (Utility) 往往是灾难性的。当你为了保护用户而添加足够的噪声时，数据会变得严重失真，以至于 GNN 很难从中通过学习获得任何有用的信息。

那么，我们如何在严格的隐私保护和高模型性能之间取得平衡呢？

在这篇文章中，我们将深入探讨一篇提出 UPGNET (效用增强型隐私图神经网络，Utility-Enhanced Private Graph Neural Network) 的研究论文。该框架直面噪声问题。通过数学分析 LDP 为何 会破坏 GNN，研究人员开发了一个包含 节点特征正则化 (NFR) 和 高阶聚合器 (HOA) 的两阶段清洗过程。

如果你是对深度学习和隐私交叉领域感兴趣的学生或从业者，这篇论文为让隐私 AI 真正可用提供了一张蓝图。

隐私与效用的拉锯战

要理解 UPGNET，我们需要先了解它所处的环境。

场景

想象一下，一个云服务器想要训练一个 GNN 进行节点分类 (例如，将用户分类为“机器人”或“人类”) 。用户拥有敏感的特征向量 (\(\mathbf{x}\)) ，比如浏览历史或个人资料详情。

在标准的中心化设置中，用户会直接将 \(\mathbf{x}\) 上传到服务器。但在本地隐私设置中，用户不信任服务器 (或者服务器希望限制其责任) 。相反，每个用户在其设备上运行一个扰动机制 \(\mathcal{M}\)。

\[ \mathbf{x} \xrightarrow{\text{LDP}} \mathbf{x}' \]

用户将带噪声的 \(\mathbf{x}'\) 发送到服务器。服务器收集这些噪声向量和图结构 (边) 来训练模型。

问题: 低效用

问题在于，现有的针对节点特征的 LDP 协议具有破坏性。由于特征向量通常是高维的，“隐私预算” (\(\epsilon\)) 必须分摊到许多维度上。这意味着每个特定属性获得的预算非常少，导致注入了大量的噪声。

当服务器尝试使用标准 GNN 聚合这些噪声数据时，结果往往很差。

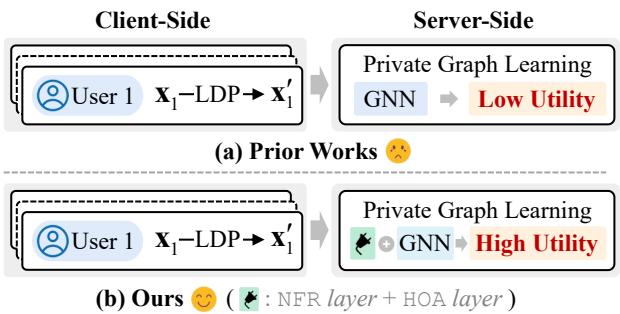
如 图 1 所示，先前的工作 (a) 通常将噪声数据直接输入 GNN，导致“哭脸”结果——低效用。UPGNET 方法 (b) 在 GNN 之前插入了一个专门的处理模块——包含 NFR 和 HOA 层——有效地从噪声中恢复了信号。

根本原因: 为什么 LDP 会破坏 GNN？

研究人员并没有仅仅猜测解决方案；他们首先对误差进行了理论分析。他们将流程建模为三个阶段: 扰动 (客户端) 、校准 (服务器端调整) 和聚合 (GNN 消息传递) 。

关键问题是: 什么因素驱动了“估计误差”？这个误差是 GNN 应该 计算出的嵌入 (使用干净数据) 与它 实际 计算出的嵌入 (使用噪声数据) 之间的差异。

利用伯恩斯坦不等式 (Bernstein’s inequality) ，作者推导出了这个误差的界限。

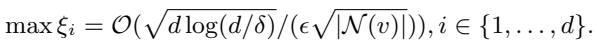
让我们仔细看看上面的公式。最大误差 (\(\xi\)) 正比于:

\[ \mathcal{O}\left( \frac{\sqrt{d \log(d)}}{\epsilon \sqrt{|\mathcal{N}(v)|}} \right) \]

如果我们去掉常数，我们会发现控制误差的两个关键杠杆:

1. 特征维度 (\(d\)): 误差随着特征数量的增加而增加。高维数据更难进行隐私化处理，因为噪声会淹没稀疏的信号。
2. 邻域大小 (\(|\mathcal{N}(v)|\)): 误差随着邻域大小的增加而减小。这在直觉上是说得通的: 如果你对 100 个邻居的噪声特征取平均值，噪声相互抵消的效果要比只对 2 个邻居取平均值好得多。

洞察: 要修复隐私图学习，我们必须有效地降低特征维度并增加有效邻域大小 。

解决方案: UPGNET

基于这一分析，作者提出了 UPGNET。这是一个位于噪声数据和 GNN 模型之间的框架。它由两个即插即用的层组成，专门用于操纵这两个变量 (\(d\) 和 \(|\mathcal{N}(v)|\)) 。

如 图 2 所示，UPGNET 可以通过两种架构进行排列: H-N (HOA 后接 NFR) 或 N-H (NFR 后接 HOA) 。让我们分解这两个核心组件。

组件 1: 节点特征正则化 (NFR)

目标: 降低有效特征维度 (\(d\))

标准的 LDP 机制会向 每个 维度添加噪声。如果一个用户的特征向量长度为 1,000，但只有 10 个特征是非零的，LDP 机制仍然会扰动那些零值，将稀疏向量变成充满噪声的稠密向量。

节点特征正则化 (NFR) 层旨在通过引入稀疏性来对该向量进行去噪。它依赖于机器学习中的经典技术: \(L_1\)-正则化 。

目标是找到节点特征的更清晰表示，既要忠实于噪声输入，又要保持稀疏性。研究人员制定了一个损失函数，结合了与噪声输入的距离和 \(L_1\) 惩罚项 (它强制小数值归零) 。

通过使用近端梯度下降 (Proximal Gradient Descent) 求解这个优化问题，他们推导出了一个充当 软阈值 (Soft Thresholding) 算子的闭式解。

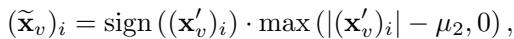
看上面的方程。对于每个特征 \(i\)，新值的计算方法是取噪声值 \((\mathbf{x}'_v)_i\) 并减去阈值 \(\mu\)。

• 如果噪声值小于 \(\mu\)，它会被钳制为 0。
• 如果它大于 \(\mu\)，则减去 \(\mu\)。

这实际上充当了守门员的角色。由于 LDP 噪声通常表现为散布在零周围的随机值，这个“特征选择”步骤擦除了纯噪声维度 (降低了有效 \(d\)) ，同时保留了超过噪声底限的强信号。

组件 2: 高阶聚合器 (HOA)

目标: 扩展有效邻域大小 (\(|\mathcal{N}(v)|\))

理论分析表明，较大的邻域可以减少误差。然而，大多数现实世界的图都是稀疏的；节点通常只有很少的直接邻居。

一个简单的解决方案是堆叠多层 GNN，从邻居的邻居 (多跳) 聚合信息。这通常被称为 简单 K 跳聚合 (Simple K-hop Aggregation, SKA) 。 SKA 的问题在于 过平滑 (Over-smoothing) 。

过平滑陷阱

当你聚合越来越多的跳数 (K 增加) 时，图中所有节点的表示开始变得相同。它们收敛到一个全局平均值。在隐私设置中，这更糟糕，因为噪声会扩散到各处。

研究人员使用 狄利克雷能量 (Dirichlet Energy) 对此进行了分析，这是一个衡量节点嵌入与其邻居差异程度的指标。他们发现，标准聚合会导致这种能量非常快地下降到零 (完全平滑) 。

HOA 算法

高阶聚合器 (HOA) 通过使用个性化聚合方案解决了这个问题。它不是将 10 跳邻居与 1 跳邻居同等对待，而是保持与局部结构的强连接。

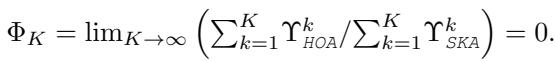
上面的数学公式证明，HOA 与 SKA 中的狄利克雷能量之比趋近于零，这意味着 HOA 对标准聚合中出现的无节制能量衰减 (过平滑) 具有更强的抵抗力。

简单来说: HOA 允许模型向远处看 (大 \(K\)) 以收集足够的数据点来抵消隐私噪声，同时不会 冲刷掉中心节点的独特特征。

实验与结果

UPGNET 真的有效吗？作者在 Cora、Citeseer、LastFM 和 Facebook 等标准数据集上对其进行了测试，并将其与最先进的隐私 GNN 方法 (LPGNN, Solitude) 进行了比较。

1. 整体性能

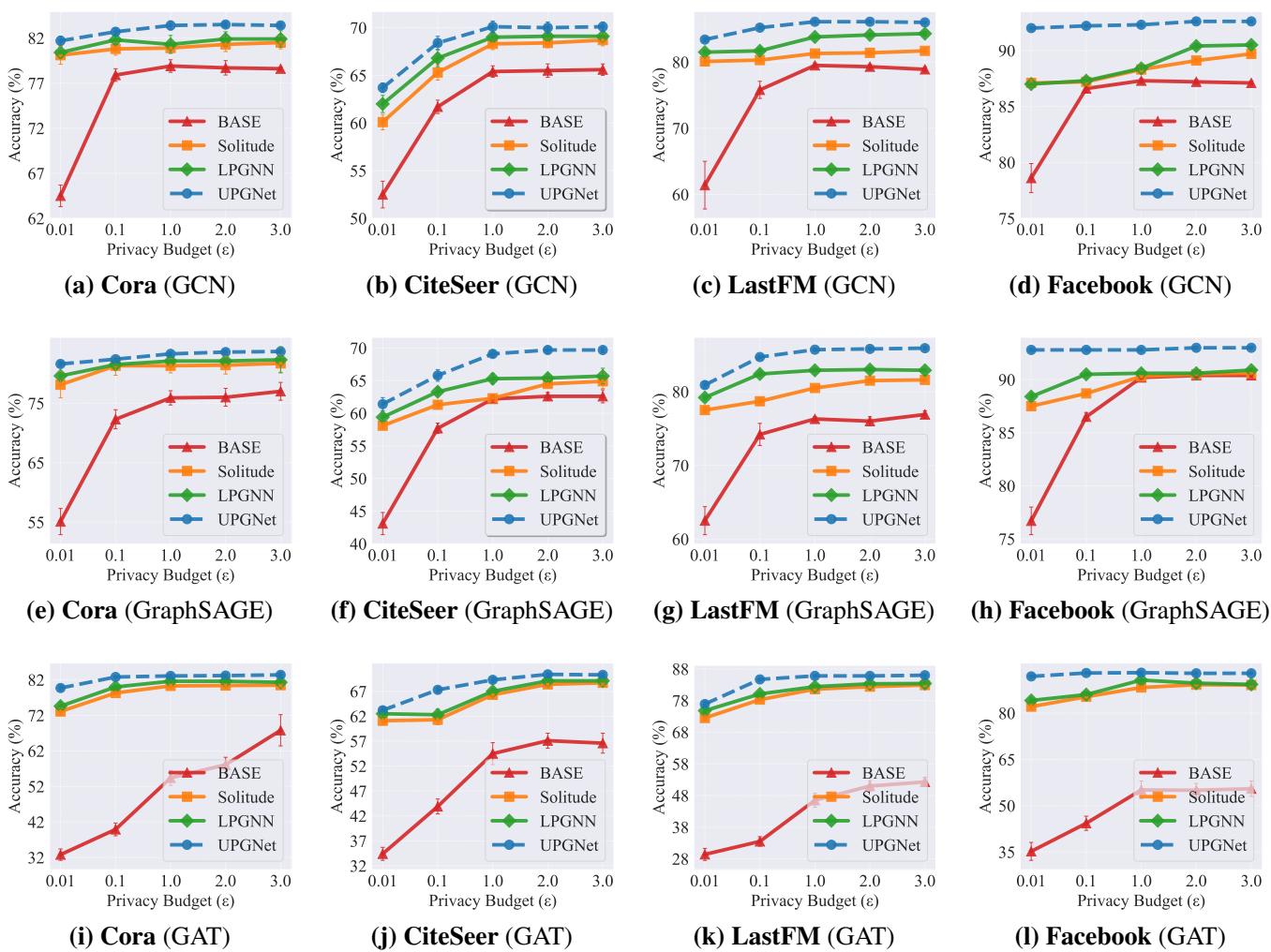
图 3 显示了测试准确率与隐私预算 (\(\epsilon\)) 的关系。请记住，更低的 \(\epsilon\) 意味着更严格的隐私 (更多噪声) 。

• 蓝色圆圈 (UPGNET) 始终处于顶部。
• 看 图表 (c) LastFM : 在严格的隐私水平下 (\(\epsilon=0.1\)) ，UPGNET 保持了比基线 (LPGNN 和 Solitude) 高得多的准确率，后者的表现几乎崩溃。
• 在 Facebook 数据集 (图表 d, h, l) 上，UPGNET 的表现几乎与非隐私基线一样好，有效地解决了该数据集的隐私成本问题。

2. NFR 真的有用吗？

研究人员采用了标准的扰动机制 (如分段机制 PM 和多比特机制 MBM) ，并简单地为其添加了 NFR 层。

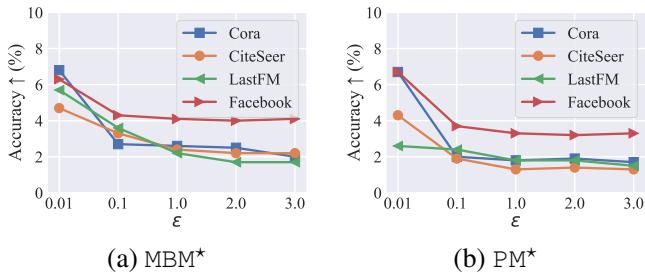
图 5 可视化了 NFR 提供的“提升”。曲线显示了准确率的 增加。

• 注意，当 \(\epsilon\) 较低时 (x 轴左侧) ，提升幅度最大。
• 这证实了当噪声最大时，NFR 的“去噪/阈值化”效果最有价值。

3. HOA 真的解决了过平滑吗？

这可能是最有趣的结果。他们将 HOA 与标准的简单 K 跳聚合 (SKA) 进行了比较，同时增加了跳数 (\(K\)) 。

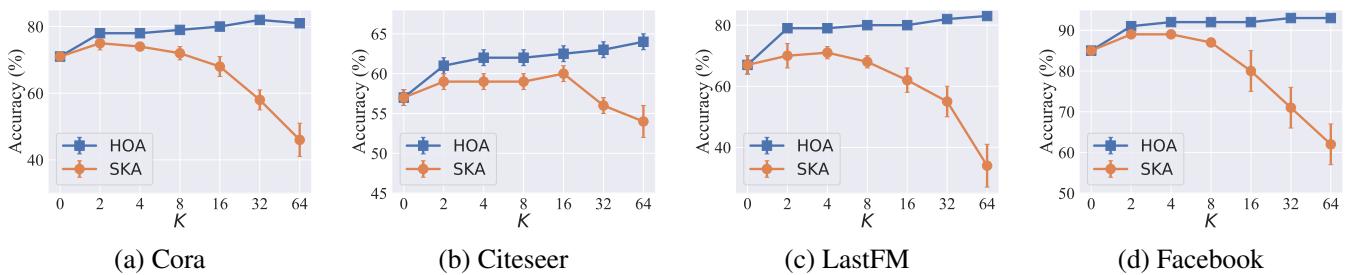
在 图 6 中，看 橙色线 (SKA) 。 随着 \(K\) 变大 (向右移动) ，准确率崩溃。这就是实际中的过平滑；模型将所有东西都模糊在一起了。 现在看 蓝色线 (HOA) 。 即使在 \(K=64\) 时，准确率仍在攀升或保持稳定。这证明 HOA 成功地扩展了邻域以抵消噪声，且没有破坏信号结构。

4. 异配图 (Heterophilic Graphs)

大多数 GNN 假设“同配性” (朋友是相似的) 。但是对于连接的节点截然不同 (异配性) 的图呢？

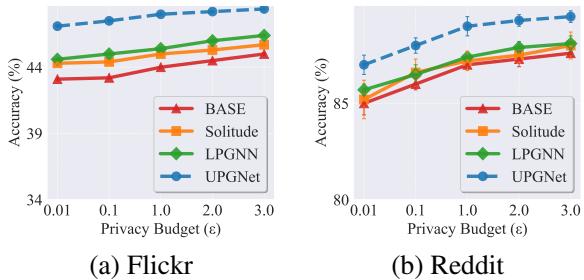
图 7 显示了在 Flickr 和 Reddit (异配数据集) 上的结果。UPGNET 在这里也保持了领先地位。因为 HOA 保留了狄利克雷能量 (邻居之间的差异) ，它防止了模型将相连但不相似节点的独特特征平均化。

结论

论文《Going Deeper into Locally Differentially Private Graph Neural Networks》全面诊断了隐私为何会损害 GNN: 维度太多和邻居太少 。

通过引入 UPGNET , 作者提供了一个稳健的解决方案:

1. NFR 充当过滤器，利用 \(L_1\)-正则化剥离高维空间中的噪声。
2. HOA 充当望远镜，允许节点从远处的邻居收集去噪信息，而不会遭受过平滑带来的模糊。

对于学生和研究人员来说，这项工作强调了将隐私防御与数据的特定数学属性相结合的重要性。我们不能简单地添加噪声并祈祷好运；我们需要架构上的改变——如 NFR 和 HOA——来恢复我们关心的效用。

UPGNET 证明，通过正确的后处理，我们不必在保护用户数据和构建智能模型之间做选择。我们可以两者兼得。

---