模拟原子世界是计算科学的圣杯之一。从发现新的电池材料到设计新型药物，分子动力学 (Molecular Dynamics, MD) 模拟让我们能够观察原子随时间推移的运动。历史上，科学家们不得不在两个极端之间做出选择: 量子力学方法 (高度精确但极其缓慢) 或经典力场 (快速但往往不准确) 。

近年来，第三个竞争者出现了: 机器学习原子间势 (Machine Learning Interatomic Potentials, MLIPs) 。 特别是等变 MLIPs (Equivariant MLIPs) , 通过以显著更高的效率实现量子级精度，彻底改变了该领域。它们遵循物理学的对称性定律——如果你旋转一个分子，作用在上面的力也应该随之旋转。

然而，“更高的效率”是相对的。这些模型的计算量仍然很大。训练它们可能需要数天时间，而推理速度往往限制了我们可以模拟的分子系统的大小。罪魁祸首是什么？是一个被称为张量积层 (Tensor-Product layer) 的特定数学运算。

在这篇文章中，我们将深入探讨 FlashTP , 这是首尔大学的研究人员在 ICML 2025 上发表的一个新库。FlashTP 系统地解决了张量积层的低效问题，实现了巨大的加速 (在特定内核上高达 40 倍) ，并使得模拟数千个原子的系统成为可能，而这在以前由于内存限制是不可能实现的。

背景: 原子智能的架构

要理解 FlashTP 如何 工作，我们首先需要理解它正在加速 什么。

MLIP 流水线

从高层次来看，MLIP 模型的功能类似于势能面的函数逼近器。给定一组原子位置及其原子序数 (类型) ，模型预测系统的总势能。

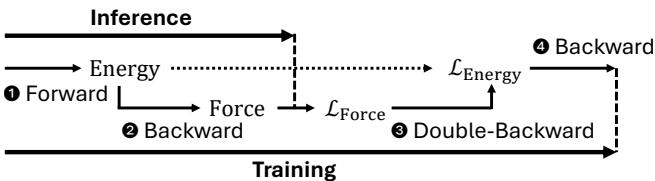
图 1. MLIP 模型推理和训练流水线概览。

如图 1 所示，该过程涉及两个明显的阶段:

  1. 前向传播 (能量预测) : 模型接收原子图并输出一个能量标量。
  2. 反向传播 (力计算) : 因为力是能量的负梯度 (\(F = -\nabla E\)) ，我们通过计算预测能量相对于原子位置的梯度来计算力。

在训练期间，情况变得更加复杂。为了更新模型权重，我们需要计算能量和力的损失。由于力已经是梯度的导数，针对力的损失进行训练需要“双重反向 (double-backward) ”传递 (梯度的梯度) 。这使得反向和双重反向传播在计算上至关重要。

等变模型的结构

像 NequIP、MACE 和 SevenNet 这样的最先进模型是建立在图神经网络 (GNNs) 之上的。在这些图中，原子是节点，邻居之间的相互作用是边。

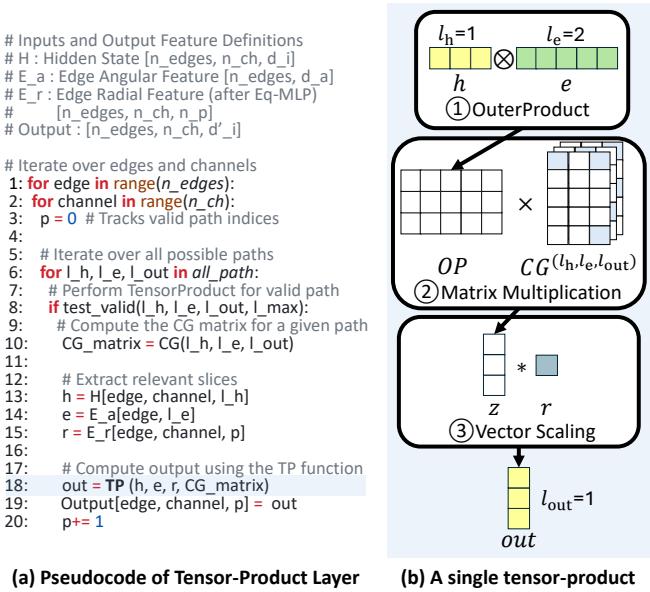
图 2. 等变 MLIP 模型架构。

图 2 展示了典型的架构。模型由一堆“相互作用块 (Interaction Blocks) ”组成。在每个块内部，信息在原子之间交换以更新它们的内部表示 (隐藏状态) 。这种消息传递机制允许原子“学习”其局部环境。

这种消息传递的核心是张量积层 (在图 2b 中标记为步骤 4) 。该层将来自节点 (原子) 的特征与来自边 (关于邻居的角度和径向信息) 的特征相结合，以产生新的表示。

数学瓶颈: 张量积

为什么这一层如此昂贵？这归结为维持等变性 (equivariance) 的复杂性。为了确保物理规律在旋转下保持不变，我们不能简单地相乘向量。我们必须使用特定的规则组合“几何张量”。

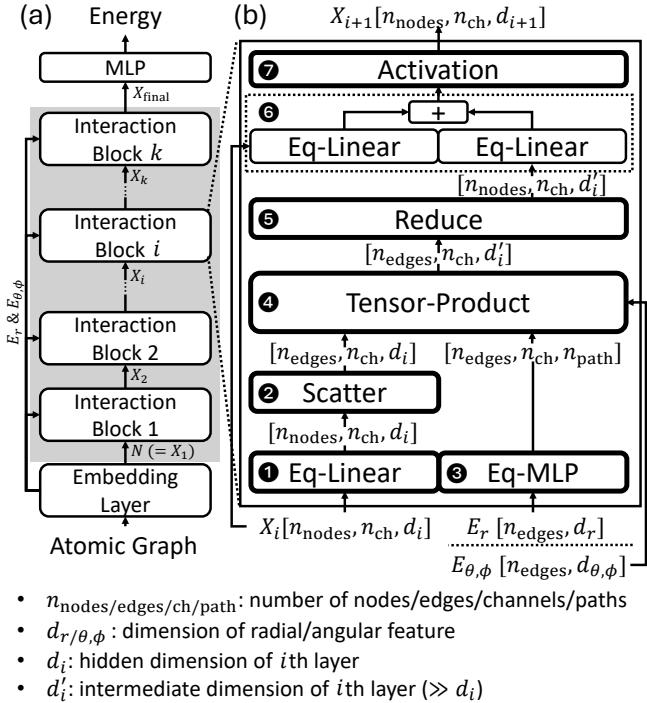
图 3. 张量积层及单个张量积操作概览。

图 3 分解了该操作。单个张量积层涉及为图中的每条边、跨多个通道和“路径”执行许多单独的张量积运算。

一条路径由输入阶数 (\(l_h\) 代表隐藏节点特征，\(l_e\) 代表边特征) 和期望的输出阶数 (\(l_{out}\)) 的组合定义。 计算包括:

  1. 外积 (Outer Product) : 从输入向量创建一个巨大的临时矩阵。
  2. Clebsch-Gordan (CG) 乘法: 将该矩阵乘以 CG 系数——这是源自量子力学、用于强制旋转对称性的常数值。
  3. 缩放 (Scaling) : 应用一个可学习的权重。

这种操作在数学上很优雅，但在计算上却很残酷。随着特征阶数 (\(l_{max}\)) 的增加以捕捉更精细的物理细节，路径的数量和计算规模呈指数级增长。

识别低效之处

FlashTP 论文的作者分析了最先进模型 SevenNet-13i5 的性能，发现张量积层是无可争议的瓶颈。

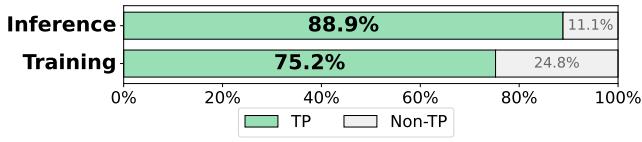
图 4. SevenNet-l3i5 推理和训练中张量积层的占比。

如图 4 所示，这一层消耗了近 89% 的推理时间和 75% 的训练时间 。 如果你想加速 MLIPs，你必须修复张量积。

研究人员确定了三个主要的低效来源:

  1. 内存流量 (带宽墙) : 该操作生成巨大的中间张量 (外积的结果) ，这些张量被写入 GPU 内存，结果只是为了在下一步立即被读回。
  2. 内存峰值 (容量墙) : 张量积层的输出通常比输入大一个数量级。即使随后的层 (Reduce) 会对其进行压缩，GPU 也必须分配足够的内存来保存完整的未压缩输出，导致在大图上出现内存溢出 (OOM) 错误。
  3. 无效计算 (稀疏性问题) : 用于强制对称性的 Clebsch-Gordan 矩阵非常稀疏。大多数值为零。标准矩阵乘法在乘以零上浪费了时间。

让我们看看资源利用率来证实这一点:

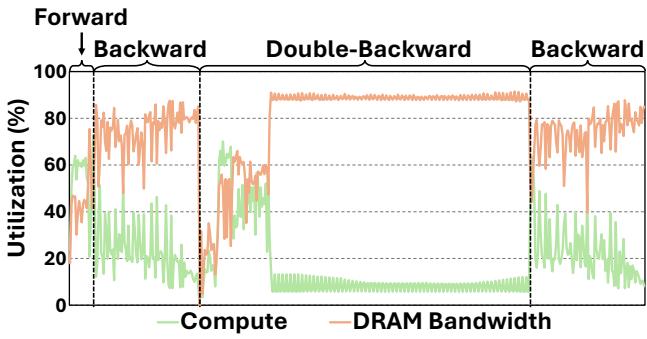
图 6. NVIDIA A100 GPU 上 SevenNet-l3i5 中张量积层的计算和 DRAM 带宽利用率。

图 6 揭示了一个说明性的故事。在反向和双重反向传播期间 (对于训练和力计算至关重要) ，GPU 处于内存受限 (memory bound) 状态 (橙色线很高) ，而计算利用率 (绿色线) 下降。GPU 渴望数据，只能等待缓慢的内存访问，而不是在处理数字。

FlashTP 解决方案

FlashTP 通过三种独特的优化策略解决了这些瓶颈: 算子融合 (Kernel Fusion) 、稀疏感知计算 (Sparsity-Aware Computation) 和路径聚合 (Path-Aggregation) 。

1. 算子融合 (Kernel Fusion)

解决内存带宽问题的第一步是停止将中间数据写入主 GPU 内存 (DRAM) 。

在标准实现 (如 PyTorch 或 e3nn) 中，张量积和随后的“Reduce” (对邻居的贡献求和) 是独立的算子 (kernel) 。张量积将一个巨大的张量写入内存，Reduce 算子再将其读回以进行求和。

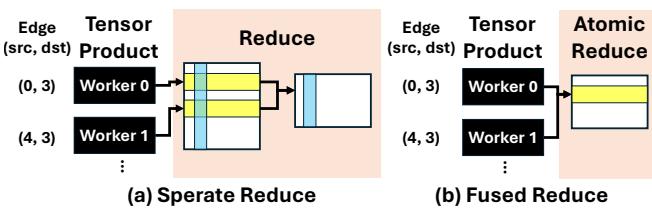
图 7. 张量积层输出阶段的比较。

FlashTP 采用了算子融合 。 如图 7 所示，它将张量积计算与归约 (Reduction) 步骤直接融合。

  • 之前 (a): 每个 worker 计算其结果，将其写入缓冲区。随后，归约步骤读取所有缓冲区并求和。
  • 之后 (b): worker 计算结果并使用原子操作 (atomicAdd) 立即将其添加到内存中的目标累加器中。

这完全消除了存储巨大中间输出张量的需求。这同时解决了内存流量问题和内存峰值问题。

2. 利用稀疏性

Clebsch-Gordan (CG) 系数是由物理学决定的常数。它们告诉我们量子态如何耦合在一起。关键是，它们充满了零。

表 1. 不同 l_max 下 CG 系数矩阵的稀疏性。

如表 1 所示，随着阶数 (\(l_{max}\)) 的增加，稀疏度范围从 71% 到 86% 。 标准的密集矩阵乘法会对所有这些条目执行运算，浪费了大量的计算能力。

FlashTP 实现了针对这种特定结构优化的自定义稀疏矩阵乘法。

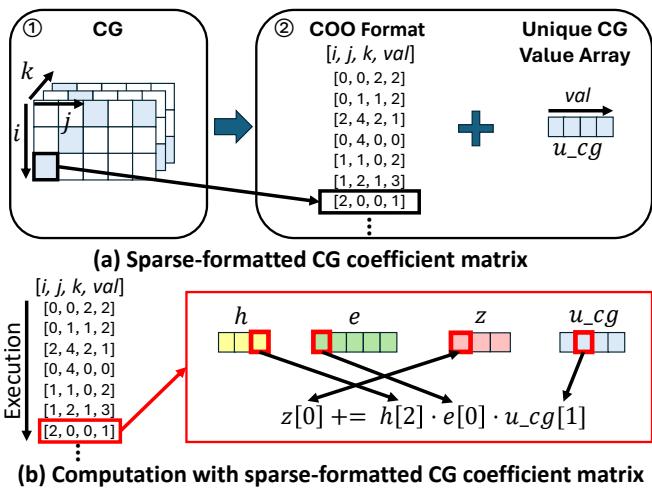
图 8. FlashTP 中稀疏张量积的实现。

图 8 详细介绍了他们的方法:

  1. 存储: 他们使用坐标格式 (COO) 仅存储非零索引 \((i, j, k)\)。
  2. 压缩: 由于许多非零 CG 值是重复的，他们将唯一值存储在一个小的查找表 (u_cg) 中，并在矩阵中仅存储 8 位索引。这大大减少了系数的内存占用。
  3. 执行: 内核仅迭代非零列表，仅在必要时执行计算。

3. 路径聚合 (Path-Aggregation)

在修复了算子融合和稀疏性之后，一个新的瓶颈出现了: 读取输入特征。

回想一下，张量积层由许多“路径”组成。例如，1 阶隐藏特征可能与 1 阶边特征相互作用，产生 0 阶输出、1 阶输出和 2 阶输出。这是三条不同的路径，使用完全相同的输入向量。

在朴素的实现中，GPU 会从内存中三次分别读取输入向量。

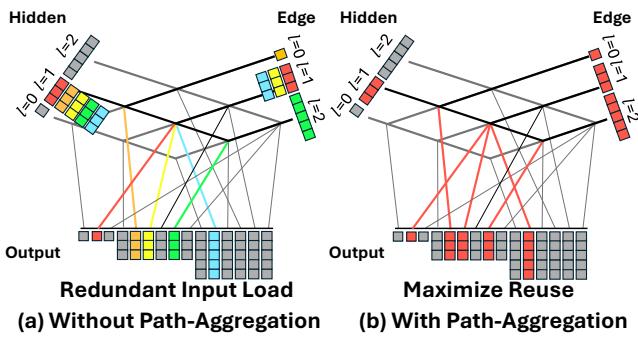
图 9. 路径聚合效果的可视化。

FlashTP 引入了路径聚合 (图 9) 。通过预先分析计算图，FlashTP 将所有共享相同输入组件的路径分组。它将输入数据加载到快速的 GPU 寄存器/共享内存中一次，然后背靠背执行所有依赖路径。

在图 9 所示的示例中，这将隐藏特征的内存读取次数减少了 5 倍，边特征的读取次数减少了 3 倍。

实现与易用性

编写自定义 CUDA 内核很困难，将它们集成到高级 Python 工作流中可能会很混乱。作者将 FlashTP 设计为 e3nn 的即插即用替代品，e3nn 是最流行的等变神经网络库。

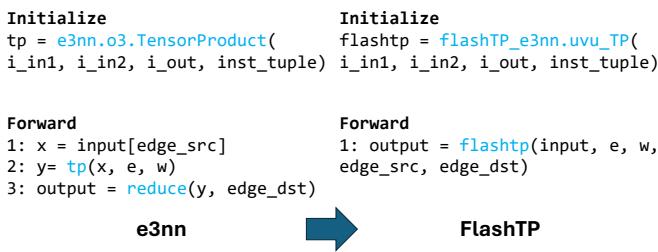
图 10. 将 FlashTP 集成到基于 e3nn 框架的现有实现所需的代码更改。

如图 10 所示，采用 FlashTP 只需要极少的代码更改。接口模仿了 e3nn.o3.TensorProduct 类，保留了模型结构和矩阵排序。这使得研究人员可以在不重写整个代码库的情况下加速现有模型。

实验结果

那么，它有多快？结果全面令人印象深刻。

微基准测试加速比

首先，看看与 e3nn 和 NVIDIA 自家的 cuEquivariance (cuEq) 库相比的原始内核性能:

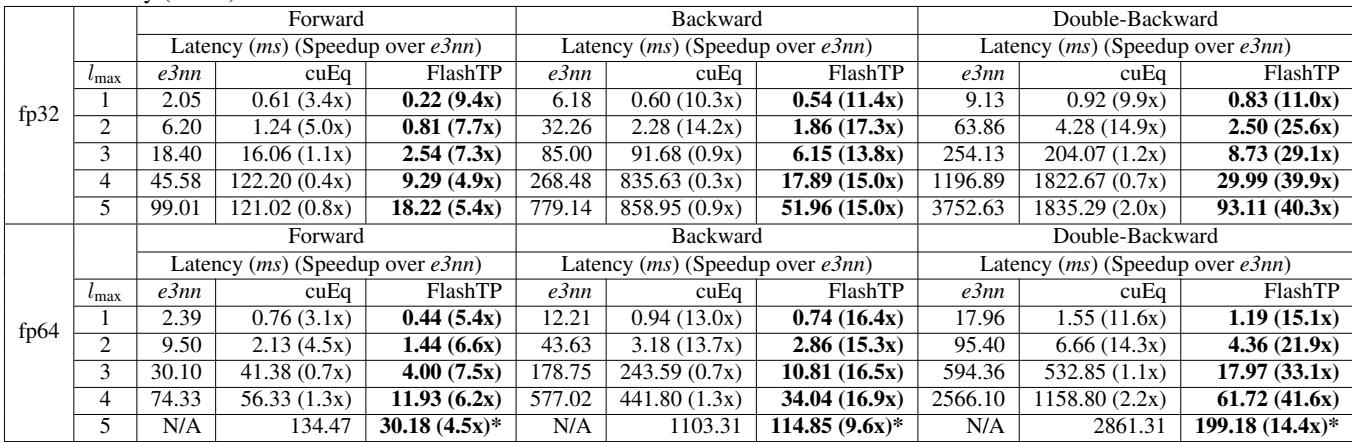
表 2. 不同张量积配置的加速比比较。

表 2 凸显了 FlashTP 的优势。

  • 前向传播: 比 e3nn 快高达 9 倍 。
  • 反向/双重反向传播: 这是 FlashTP 大放异彩的地方，显示出 20 倍到 40 倍的加速。因为反向传播严重受限于内存，算子融合和路径聚合策略在此带来了巨大的红利。
  • 与 NVIDIA cuEq 的比较: 虽然 cuEq 在低阶 (\(l_{max}=1,2\)) 时很快，但它难以扩展。对于 \(l_{max}=5\)，FlashTP 明显更快，而且重要的是，避免了困扰基准线的内存溢出 (OOM) 错误。

贡献最大的是什么？

一项消融实验 (图 11) 分解了这些收益。

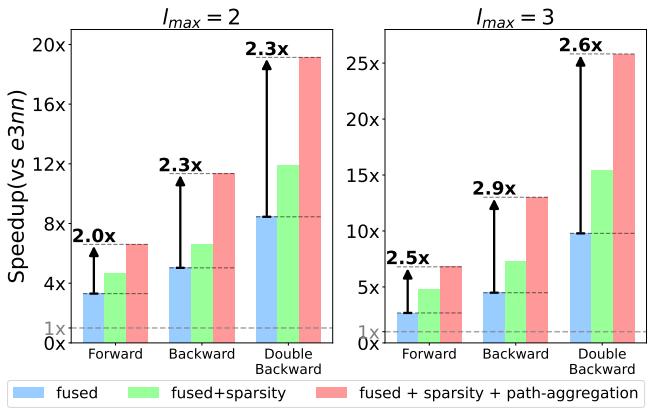
图 11. 三种优化技术的消融研究结果。

  • 蓝色 (Fused) : 仅融合就提供了稳固的 3-10 倍提升。
  • 绿色 (Fused + Sparse) : 增加稀疏性在前向传播中帮助显著，因为相对于内存，那里的计算更重。
  • 红色 (Fused + Sparse + Path) : 路径聚合 (红色条) 提供了最后的飞跃，特别是在双重反向传播 (最右边的集群) 中，将加速比从约 15 倍推高到近 30 倍 。

现实世界的影响: MD 模拟

加速内核很棒，但这能帮助科学家运行更大的模拟吗？

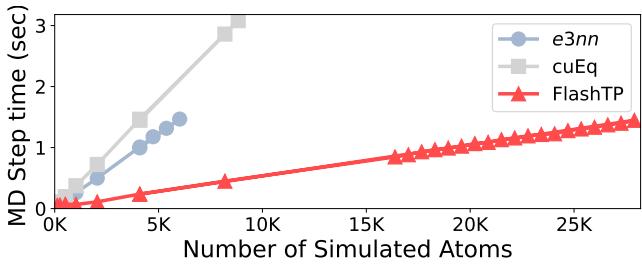
图 12. 不同铜原子数量下的平均 MD 模拟步骤时间比较。

图 12 显示了随着原子数量增加，每一步 MD 所需的时间。

  • e3nn (蓝色) : 撞上内存墙并崩溃 (OOM) ，大约在 6,000 个原子时。
  • cuEq (灰色) : 扩展性稍好，但在约 9,000 个原子时崩溃。
  • FlashTP (红色) : 显示出线性扩展，轻松处理超过 26,000 个原子 。

FlashTP 不仅对于 4,000 个原子的系统快了约 4.2 倍 , 而且还将峰值内存使用量减少了 6.3 倍 , 从而允许模拟以前因太大而无法放入 GPU 的系统。

训练加速

最后，对于训练自己势函数的研究人员来说，FlashTP 大幅缩短了迭代时间。

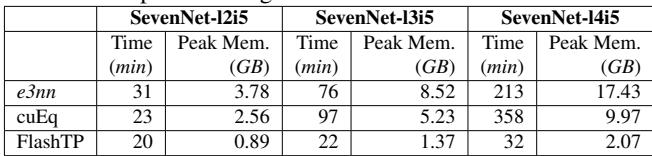
表 3. GPU 上 SevenNet 模型的每 epoch 训练时间。

表 3 显示，使用 FlashTP 训练复杂的 SevenNet-14i5 模型 (\(l_{max}=4\)) 比 e3nn 快 6.7 倍 , 将每 epoch 时间从 213 分钟降至仅 32 分钟。这将为期一周的训练运行变成了单日工作。

结论

FlashTP 代表了等变 MLIPs 的重大飞跃。通过将张量积层视为系统问题而不仅仅是数学问题，作者发现内存移动而非算术运算才是真正的限制。

通过算子融合 , 他们最大限度地减少了内存写入。通过稀疏感知 , 他们消除了无用的数学运算。通过路径聚合 , 他们最大化了数据重用。其结果是一个不仅加速了当前模型，而且扩展了可能性的视野的库——使得更大、更复杂的分子模拟能够在商用硬件上运行。

对于材料科学和机器学习领域的学生和研究人员来说，FlashTP 是一个强大的工具，它消除了使用高精度等变模型的计算负担，可能会加速下一代材料的发现。