引言

在人类的学习方式中，“知道猫是什么”与“知道猫不是什么”之间存在着明显的区别。当你想象一只猫时，你是在识别一组特定的特征——胡须、尖耳朵、尾巴。你并不是通过观察整个宇宙并排除狗、汽车和树木来定义猫的。

然而，传统的机器学习分类通常是后一种工作方式。一个标准的神经网络分类器，当被训练用来区分两个类 (比如类 1 和类 2) 时，通常会将整个特征空间切割成两个区域。数据宇宙中的每一个点都必须属于类 1 或类 2。

这就导致了一个根本性的问题: 空白区域会发生什么？那些看起来既不像猫也不像狗的海量数据区域会怎样？在标准网络中，这些区域被任意分配给了其中一个类，导致对无意义输入的过度自信。

研究论文 《Discovering a Zero (Zero-Vector Class of Machine Learning)》 提出了一个视角的迷人转变。作者建议我们不应再将“类”仅仅视为标签，而应开始将它们视为数学向量空间中的向量 。

通过严格定义这个向量空间，研究人员偶然发现了一个深刻的问题: 如果类是向量，那么零向量 (Zero-Vector) 是什么？在机器学习分类的语境中，什么是“虚无”的数学等价物？

他们找到的答案——Metta类 (Metta-Class) ——提供了一个学习“真实”数据流形的新框架，使神经网络能够说“我不知道”，并允许模块化、持续的学习。

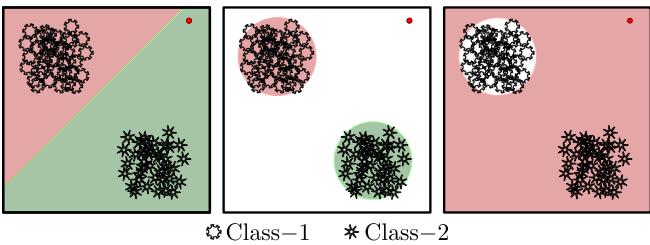
如图 1 所示，标准网络 (最左) 将整个空间二分。这项研究的目标 (中间) 是学习紧凑、准确的区域，以代表数据的真实本质。

1. 背景: Logit 概览

要理解我们如何得到“零向量”，我们首先需要重新定义在神经网络语境中“类”究竟是什么。

当神经网络处理图像时，最后一层会输出称为 logits 的原始数值。这些 logits 通常通过 Softmax 或 Sigmoid 函数传递以获得概率。研究人员建议将 logits 本身视为描述该类的函数。

有效等价集

一个类不是由单一方程定义的。如果你有一个描述数据的概率密度函数 (PDF) \(f(x)\)，你会通过检查 \(f(x)\) 是否高于某个阈值来决定一个点是否属于该类。

但这里有个关键点: 许多不同的数学函数可以导致完全相同的分类决策。如果你用一个常数缩放函数或移动它，只要你相应地调整阈值，决策边界可能保持不变。

作者将有效等价集 (Valid Equivalence Set) (表示为 \([f(x)]\)) 定义为所有能对给定分布的数据进行正确分类的 logit 方程的集合。

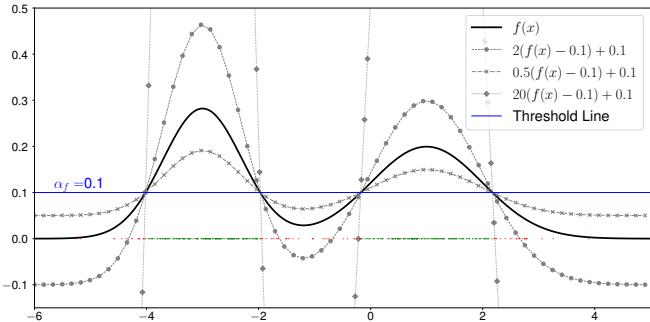
如图 2 所示，多条曲线 (实线、点线、虚线) 都可以相对于阈值线成功地对数据 (峰值) 进行分类。在这个框架中，“类向量”不仅仅是一个函数，而是这一整套有效的函数集合。

2. 核心方法: 构建向量空间

这篇论文的核心是为这些类构建一个向量空间 。 要让一组对象形成向量空间，你需要两个主要操作: 加法和标量乘法 。 作者基于集合论概念定义了这些操作。

2.1 加法即并集

当你把两个类加在一起时会发生什么？直觉上，“类 A + 类 B”应该产生一个包含 A 和 B 的超类。

在数学上，如果 \([f(x)]\) 是类-F 的向量，而 \([g(x)]\) 是类-G 的向量，它们的加法由其概率分布的并集定义。

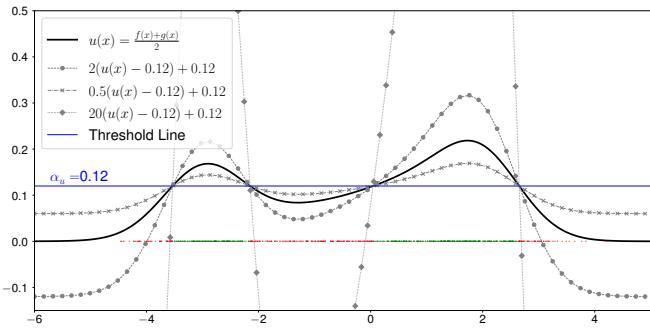
图 4 显示了结合两个类的结果。新函数 \(u(x)\) 捕获了两个原始分布的峰值。

数学定义简洁优雅:

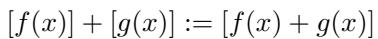
这意味着两个类等价集的向量和是它们和的等价集。

2.2 标量乘法即补集

在这个框架中，标量乘法非常迷人，因为它与集合的补集 (“非”操作) 有关。

如果你将一个类向量乘以负标量 (具体来说是 -1) ，你就反转了该函数。这有效地翻转了决策边界。之前是“正” (类内) 的区域变为“负”，而外部的区域变为内部。

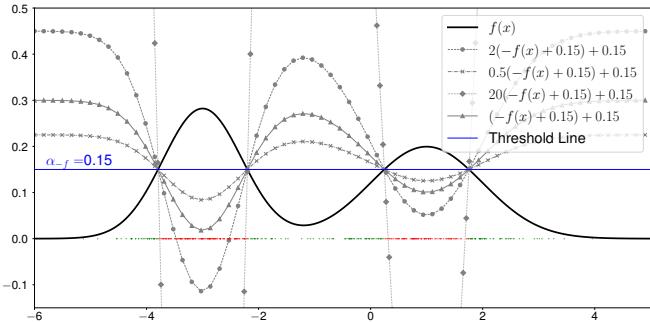
图 5 可视化了这个概念。峰变成了谷。这使得该框架能够处理像“非 类 A”这样的逻辑操作。

2.3 零向量 (Metta类) 的发现

现在我们要谈到那个关键的发现。在任何线性向量空间中，必须存在一个加法单位元——即零向量。对于任何向量 \(v\)，必须存在一个向量 \(0\) 使得:

在我们的类的语境中:

什么样的概率分布在加到另一个分布上时，能保持分类决策边界不变？

作者进行了涉及极限的严格推导。他们定义了零向量 PDF 在体积 \(\mathcal{V}\) 上的归一化常数，当该体积趋向于无穷大时。

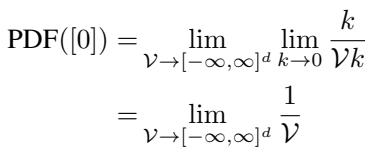
这个推导的结果是深刻的: 零向量的 PDF 是均匀分布。

这为什么讲得通？想象一下你在平原上有一座山 (你的数据类) 。如果你将整个地面高度提升一个恒定量 (加上均匀分布) ，山仍然是山。“这个点是在山上还是不在山上？”的相对判定保持不变，只要你调整你的阈值。

作者将这个零向量类命名为 Metta类 (Metta-Class) 。

实际上 Metta类是什么？

它是噪声。它是一种分布，其中的数据均匀地散布在特征空间的整个有限体积内。

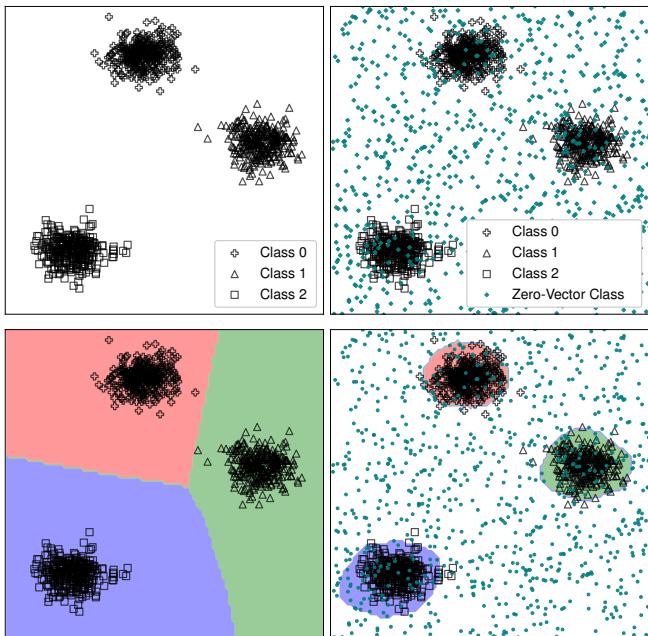
图 6 完美地说明了这一点:

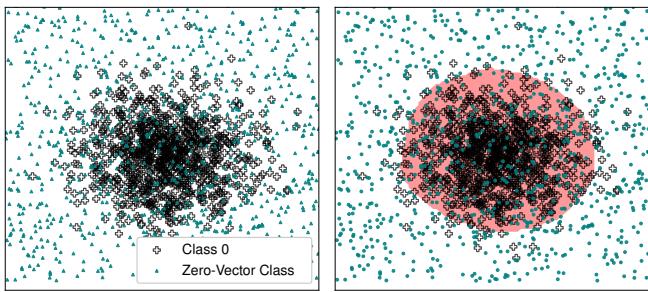
• 左上: 标准数据簇。
• 右上: 数据簇加上 Metta类 (散布在各处的青色点) 。
• 右下: 当网络包含这个“零”类进行训练时，决策边界 (彩色区域) 紧紧包裹着实际数据。空白空间被正确识别为“零” (背景/噪声) 。

3. 零向量的应用

Metta类的发现不仅仅是一个数学趣闻；它解锁了几个强大的应用，解决了深度学习中长期存在的问题。

3.1 清晰学习 (真实流形学习)

标准分类器面临“开放空间风险”——它们自信地将噪声分类为已知类，因为它们的边界延伸到了无穷远。

通过在训练期间包含 Metta类 (均匀噪声) ，我们迫使网络区分“特定类”和“随机噪声”。网络学会了仅在数据实际存在的地方推高该类的 logits。

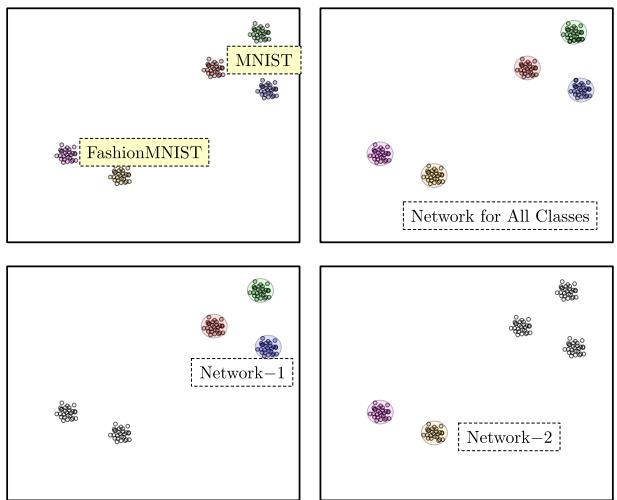
图 13 展示了这种能力。

• 网络-1 和 网络-2 (底部) : 这些网络是在特定数据集 (MNIST 和 FashionMNIST) 加上 Metta类上训练的。注意边界 (粉色和绿色) 是清晰且紧凑的。它们没有占据整个空间。
• 右上: 因为边界是紧凑的，你可以将它们叠加。这实现了模块化。

3.2 一元 (单类) 分类

你能在单个类上训练神经网络吗？通常答案是否定的——你需要一个负类来进行区分。

有了 Metta类，答案是肯定的。你将 Metta类视为“负”类。你训练一个二元分类器: 类 X 对抗 宇宙 (零向量) 。

如图 7 所示，这允许进行一元分类器训练。你可以为“猫”构建一个独立的神经网络，为“狗”构建另一个，为“车”构建再一个，所有这些都是隔离训练的。

3.3 无灾难性遗忘的持续学习

在标准 AI 中，如果你在任务 A 上训练网络，然后在任务 B 上训练它，它会忘记任务 A。这是因为权重被覆盖以最小化 B 的损失，通常会破坏为 A 设定的边界。

零向量框架提供了一个解决方案: 存储库方法 (The Repository Approach) 。 因为每个一元分类器都学习紧凑的边界并将其他所有东西视为“零”，你可以简单地将新的分类器添加到存储库中，而无需重新训练旧的分类器。

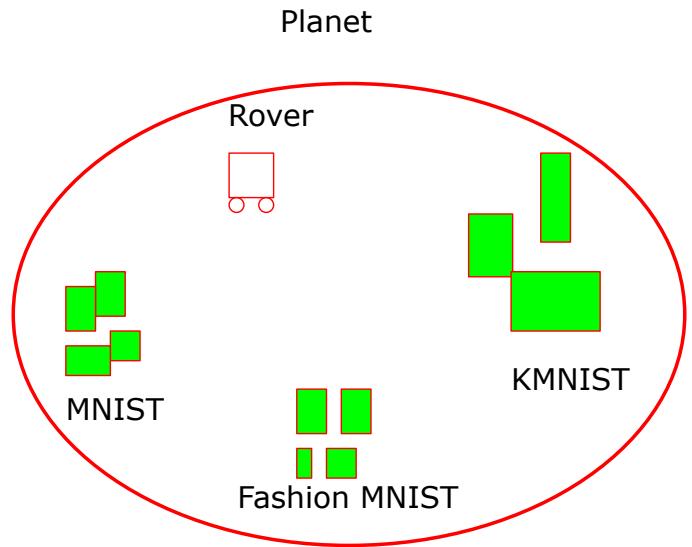
作者使用了星球上的漫游车的比喻 (图 43) 。漫游车按顺序遇到新的数据类型。它为发现的每种新类型训练一个新的“一元网络”。因为这些网络不会争夺空白空间，它们可以共存。

3.4 逻辑集合运算

由于向量空间运算对应于集合运算，我们可以对训练好的神经网络执行逻辑运算。

• 并集 (\(A \cup B\)): logit 向量相加。
• 交集 (\(A \cap B\)): 可以从并集和补集推导出来。
• 补集 (\(A^c\)): 乘以标量 -1。

这使我们能够通过简单地以数学方式组合一元网络的输出来回答复杂的查询，例如“显示属于 A 类 且 不属于 B 类的数据”。

4. 实验与指标

为了证明这种方法的有效性，作者需要新的指标。标准准确率是不够的，因为一个声称占据整个宇宙的分类器在测试集上 (如果测试集只包含类数据) 仍然可能有 100% 的准确率。

4.1 新指标: 占用因子和纯度因子

• 占用因子 (Occupancy Factor): 衡量分类器声称占据了多少“体积”。我们要这个值低 (紧密拟合) 。它是通过测试有多少噪声 (Metta类) 点被错误分类为正类来计算的。

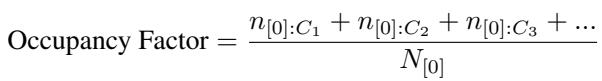
• 纯度因子 (Purity Factor): 衡量声称的区域有多“纯”。在决策边界内，是否大部分是真实数据？

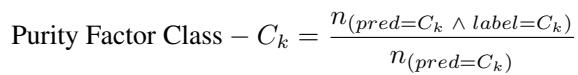
下面的图 15 和 图 16 可视化了为什么这些指标是必要的。

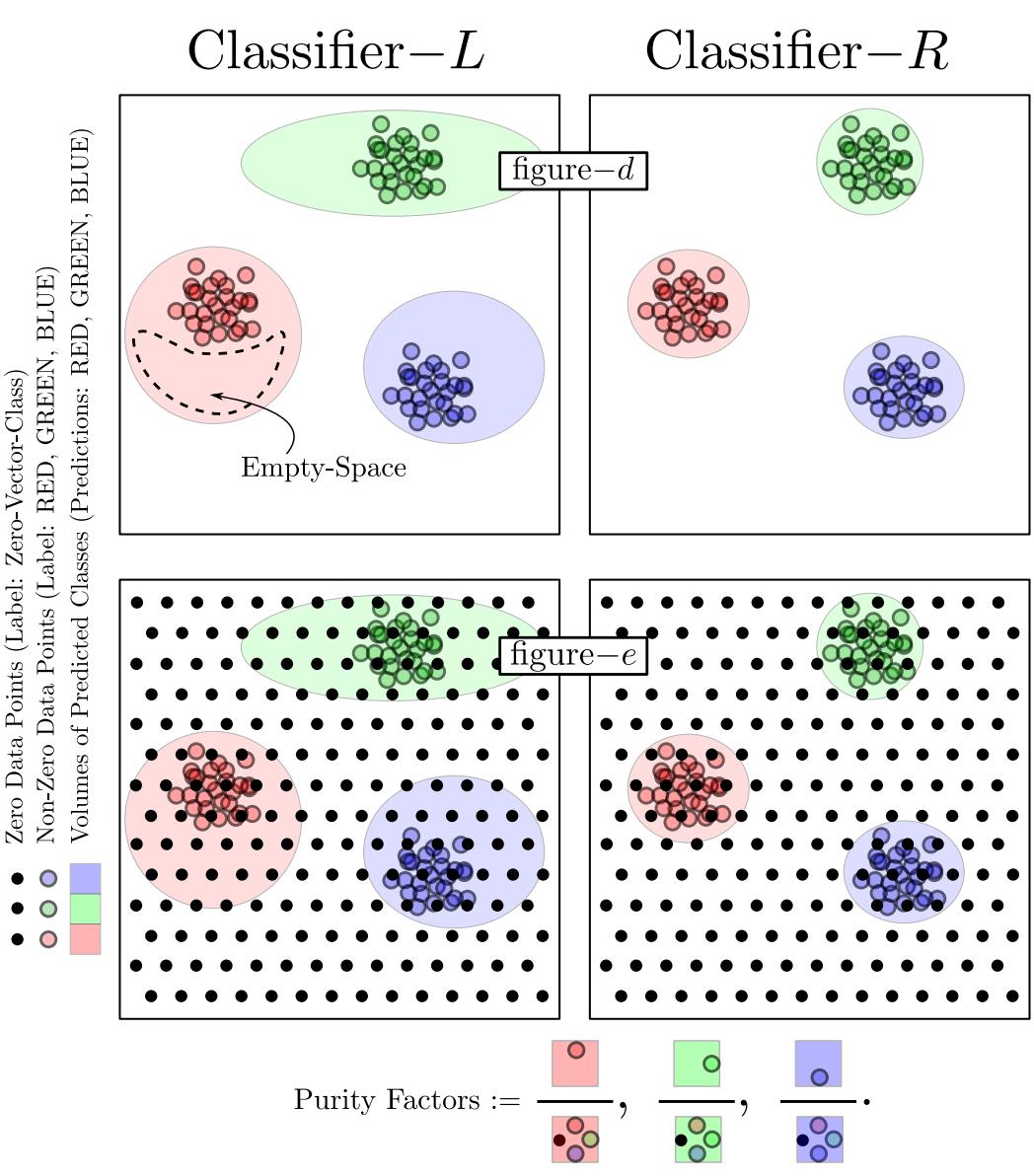
在图 15 中，分类器-L 声称了太多的空间 (高占用) 。分类器-R 更紧凑 (低占用) 。在图 16 中，分类器-L 包含了空白区域 (低纯度) 。分类器-R 紧贴数据 (高纯度) 。

4.2 MNIST 上的结果

研究人员使用 Metta类在 MNIST 数字上训练了一元分类器。

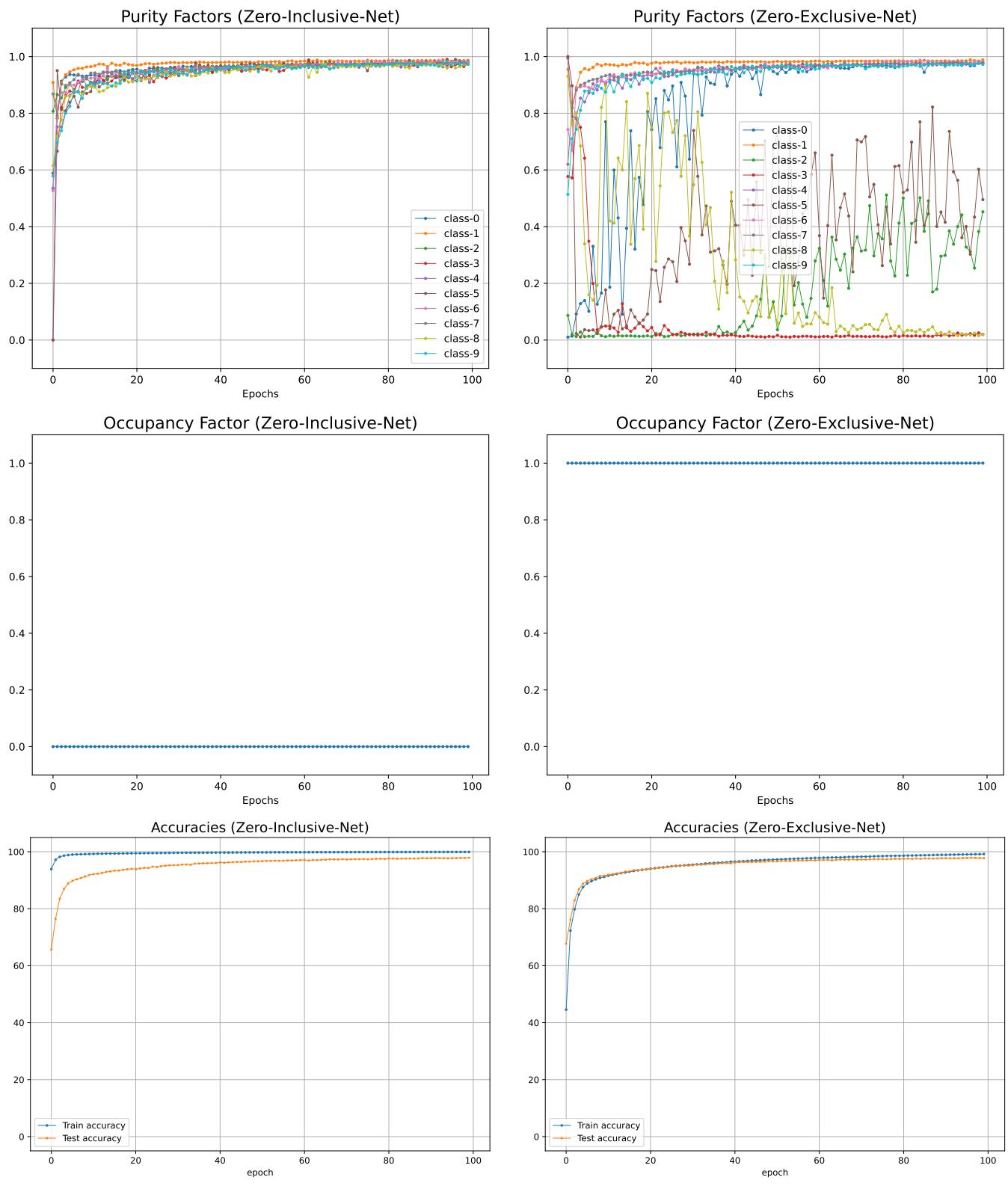
图 18 展示了结果:

• 顶行 (纯度) : 零包含网络 (左) 对所有类都实现了一致的高纯度。标准网络 (右) 则不稳定。
• 中行 (占用) : 零包含网络的占用率接近零 (它只占据必要的空间) 。标准网络的占用率为 1.0 (它占据了整个空间) 。
• 底行 (准确率) : 关键是，测试准确率保持相当。 我们获得了相同的准确率，但边界更紧凑、更有意义。

4.3 生成能力

因为网络学习的是真实的流形 (数据分布的实际形状) 而不仅仅是类之间的墙，所以 logits 的梯度指向类的“中心”。

这允许进行数据生成。通过从随机噪声开始并对类 logit 执行梯度上升，作者生成了新的图像。

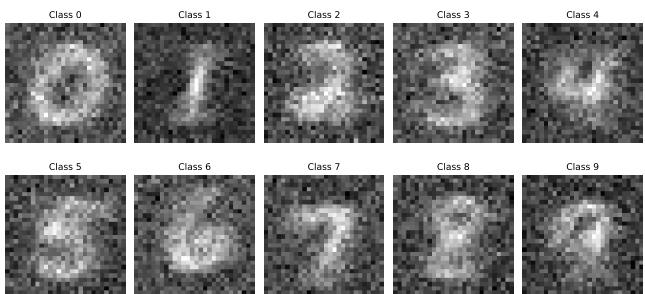
图 9 显示了仅通过跟随针对 Metta类训练的一元分类器的梯度而生成的数字。

5. 结论与启示

论文《Discovering a Zero》架起了抽象线性代数与实用深度学习之间的桥梁。通过将类形式化为向量，作者推导出零向量是均匀噪声 。

这一见解使我们能够:

1. 停止“裂脑”人工智能: 我们可以构建一元分类器的模块化存储库，而不是让一个巨大的网络试图学习所有东西 (并忘记旧东西) 。
2. 学习真实边界: 通过对抗“虚无” (Metta类) 进行训练，我们迫使网络准确地定义“存在”。
3. 结合逻辑与学习: 向量空间允许对学习到的类进行布尔运算。

虽然作者指出，扩展到像 CIFAR-10 这样的高维数据集会带来计算挑战 (需要更大的网络来维持相同的纯度) ，但该理论框架为分类问题提供了一个令人耳目一新的“第一性原理”视角。它表明，要真正理解数据，我们的机器必须首先理解围绕着它的空白空间。

在构建智能系统的探索中，事实证明，发现“零”对机器来说可能与对数学一样重要。