数学通常被视为一门讲究严密逻辑和绝对证明的学科。一个陈述要么为真，要么为假；一个定理要么已证，要么未证。然而，达成证明的过程往往是混乱的，依赖于直觉、可视化和试错。

近年来，出现了一个引人入胜的问题: 人工智能能否充当纯数学的直觉引擎？它能否“构想”出人类数学家忽略的几何构造？

Mundinger 等人最近发表的一篇题为 “Neural Discovery in Mathematics: Do Machines Dream of Colored Planes?” (数学中的神经发现: 机器会梦见彩色平面吗？) 的论文，对这一问题做出了响亮的肯定回答。研究人员解决了 哈德维格-纳尔逊问题 (Hadwiger-Nelson problem) , 这是一个位于离散几何和组合数学交叉领域的著名难题。通过将这个刚性的染色问题转化为流动的、连续的优化任务，他们利用神经网络发现了新颖的数学结构。

在这篇深度解析中，我们将探讨他们如何将一个有 70 年历史的数学问题重新表述为损失函数，他们用来“描绘”平面的架构，以及他们发现的具体、新颖的染色方案——这些方案改进了人类数十年的努力成果。

问题: 为无限染色

要理解这篇论文的贡献，我们需要先了解 哈德维格-纳尔逊 (HN) 问题 。 该问题最早于 1950 年提出，其陈述具有欺骗性的简单:

至少需要多少种颜色来为欧几里得平面 (\(\mathbb{R}^2\)) 染色，使得没有任何两个距离正好为 1 个单位的点拥有相同的颜色？

这个数字被称为 \(\chi(\mathbb{R}^2)\)，即平面的色数。

想象一下拿着一根长度为 1 的刚性棍子。无论你把这根棍子放在无限纸张的哪个位置，它的两端必须落在不同的颜色上。

尽管看似简单，这个问题至今仍未解决。

  • 下界: 我们知道至少需要 5 种颜色 (这一结果直到 2018 年才由 Aubrey de Grey 确立) 。
  • 上界: 我们知道 7 种颜色是足够的 (1950 年通过六边形镶嵌证明) 。

答案是 5、6 或 7。缩小这一差距已被证明极其实际困难，因为该问题以一种复杂的方式混合了 离散选择 (分配不同的颜色) 、连续几何 (具有不可数点的无限平面) 和 硬约束 (单位距离规则) 。

传统的计算方法，如 SAT 求解器，在这里举步维艰，因为它们需要将平面离散化为网格，这会丢失连续几何的细微差别。这正是作者提出的“神经发现”方法的切入点。

核心方法: 软化硬约束

作者的主要创新在于将这个刚性的染色问题重新表述为一个连续的优化任务，使得神经网络可以通过梯度下降来解决。

从离散到概率

在标准的染色中，一个点 \(x\) 被分配特定的颜色 \(c\)。在数学上，这是一个满足以下条件的函数 \(g: \mathbb{R}^2 \rightarrow \{1, \dots, c\}\):

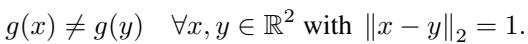
离散单位距离条件。

这个离散函数是不可微的；你无法轻松计算梯度来将点的颜色“推”向正确的方向。为了解决这个问题，研究人员放宽了约束。他们不再分配硬性的颜色，而是为平面上的每个点分配一个涵盖 \(c\) 种颜色的 概率分布 。

他们定义了一个映射 \(p: \mathbb{R}^2 \to \Delta_c\)，其中 \(\Delta_c\) 是 \(c\) 种颜色的概率单纯形。例如，如果我们测试 6 种颜色，网络会为任何给定的坐标 \((x, y)\) 输出一个包含 6 个概率值的向量。

如果点积 \(p(x)^T p(y)\) 很高，意味着点 \(x\) 和点 \(y\) 很有可能是同一种颜色。如果点积为 0，它们绝对是不同的颜色。

几何损失函数

这种方法的核心是损失函数。目标是最小化任何距离为 1 的两点共享颜色的概率。由于检查无限平面中的每一对点是不可能的，他们将优化限制在一个大的有限框 \([-R, R]^2\) 内。

损失函数 \(\mathcal{L}_R(p)\) 定义为一个积分:

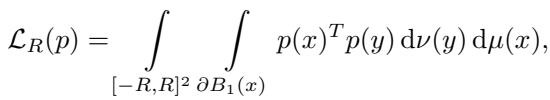
在框和单位圆上积分的连续损失函数。

让我们分解一下这个方程，因为它是整个发现过程的引擎:

  1. \(\int_{[-R, R]^2} ... d\mu(x)\) : 外部积分遍历我们边界框内的每一个“中心”点 \(x\)。
  2. \(\int_{\partial B_1(x)} ... d\nu(y)\) : 内部积分观察以 \(x\) 为圆心、半径为 1 的“球面” (圆) 。这些是所有与 \(x\) 距离正好为 1 个单位的点 \(y\)。
  3. \(p(x)^T p(y)\) : 这测量了“冲突”。它是 \(x\) 和 \(y\) 共享颜色的概率。我们希望这个值为零。

目标很简单: 找到使该损失最小化的概率染色 \(p\)。

最小化目标。

隐式神经表示

为了解决这个问题，作者使用神经网络作为函数逼近器。网络接收 2D 坐标 \((x, y)\) 作为输入，并输出颜色概率向量。这种设置被称为 隐式神经表示 (Implicit Neural Representation) 。

架构是带有 正弦激活函数 的标准多层感知机 (MLP) 。为什么要用正弦波？与 ReLU 不同，正弦激活赋予网络一种“频谱偏差 (spectral bias) ”，这意味着它天然倾向于学习平滑的、周期性的函数。由于许多几何染色 (如网格或蜂巢) 都是周期性的，这种架构非常适合该任务。

通过蒙特卡洛采样进行训练

精确计算损失函数中的双重积分在计算上是不可行的。相反，研究人员使用蒙特卡洛采样来近似梯度。

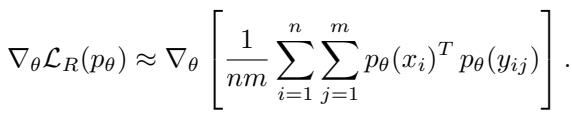
通过蒙特卡洛采样进行梯度近似。

在每个训练步骤中:

  1. 他们在框内采样 \(n\) 个随机点 (\(x_i\)) 。
  2. 对于每个 \(x_i\)，他们在周围的单位圆上采样 \(m\) 个随机点 (\(y_{ij}\)) 。
  3. 他们计算冲突概率。
  4. 他们反向传播误差以更新网络权重 \(\theta\)。

这使得网络能够探索染色空间。最初，染色是随机噪声。经过数千次迭代，网络“构想”出能够最小化单位距离冲突的模式——条纹、波浪和六边形。

案例研究 1: 平面的近乎染色

哈德维格-纳尔逊问题最有趣的变体之一问道: 如果我们只允许使用 \(k\) 种颜色 (其中 \(k < \chi(\mathbb{R}^2)\)) ，为了避免冲突，我们必须留出多少比例的平面不染色？

这就是“近乎染色 (Almost Coloring) ”问题。目标是用有限的调色板尽可能多地为平面染色。

拉格朗日松弛

为了解决这个问题，作者引入了一个“额外”颜色 (我们称之为“垃圾”颜色) 。分配给这种垃圾颜色的点不会触发单位距离冲突，但使用这种颜色会受到惩罚。

他们制定了一个约束优化问题:

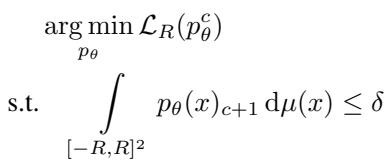
近乎染色的约束优化。

在这里，第 \((c+1)\) 种颜色是垃圾颜色。约束条件确保垃圾颜色的总面积保持在阈值 \(\delta\) 以下。在实践中，他们将其转换为拉格朗日松弛:

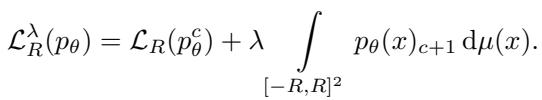
拉格朗日松弛方程。

参数 \(\lambda\) 控制权衡。如果 \(\lambda\) 很高，网络会努力最小化未染色区域。

从神经梦境到形式化证明

这篇论文的一个关键主题是，神经网络的输出不是证明；它是 候选方案 。 网络输出的染色可能肉眼看起来很完美，但包含微小的误差 (0.01% 的冲突) 。

为了将这些“梦境”转化为数学，作者开发了一个自动化流程 (算法 1) 来 形式化 结果。

  1. 初始训练: 训练网络以找到低冲突模式。
  2. 周期性提取: 分析图像以找到重复的“地砖” (一个平行四边形) 。
  3. 重新训练: 训练一个新网络，强制其在该特定地砖上呈周期性。
  4. 离散化: 将连续概率图转换为离散的像素网格。
  5. 冲突解决: 使用离散算法 (最小边覆盖) 清理导致冲突的剩余像素，将它们分配给“垃圾”颜色。

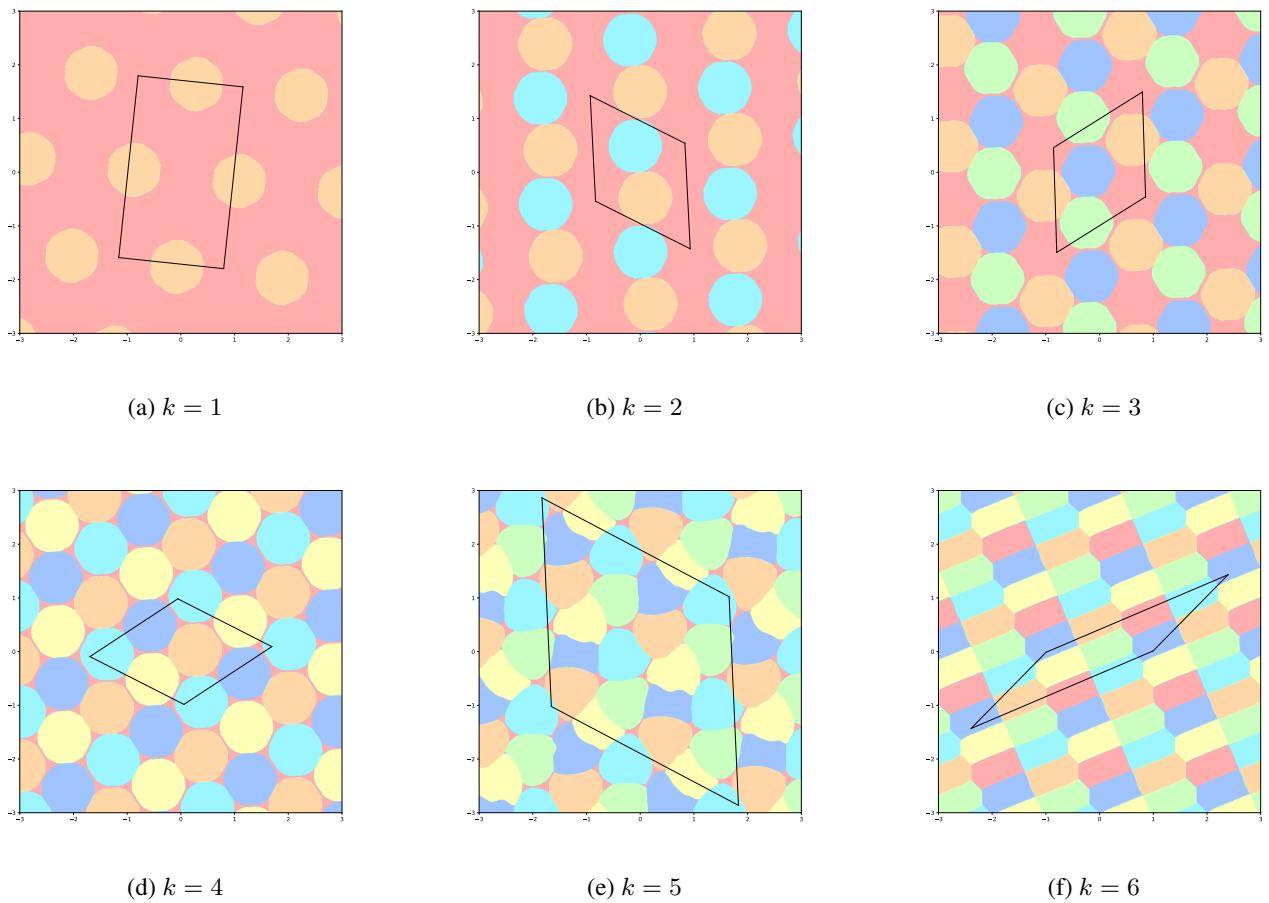
结果令人印象深刻。对于 5 色变体，以前最好的构造留下了大约 4.01% 的平面未染色。神经网络发现了一种只需移除 3.74% 平面的模式。

下面的图 10 展示了随着算法迭代，这些模式的演变过程，阐明了铺满平面的基本平行四边形域 (框) 。

显示平行四边形地砖的近乎染色演变。

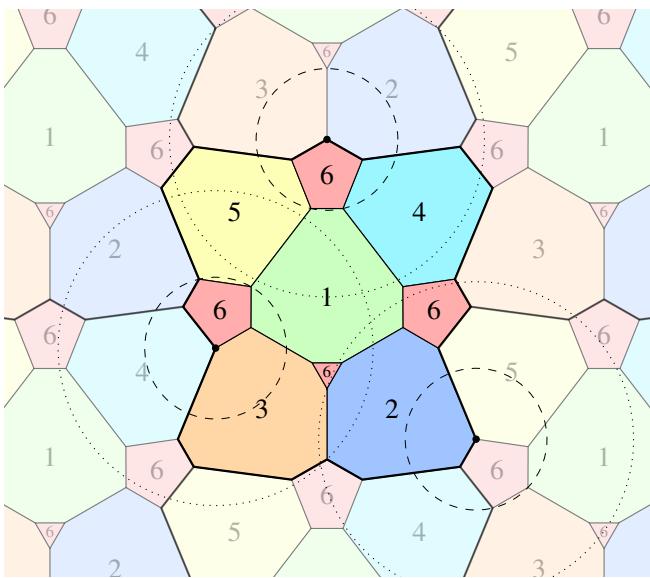
5 种颜色的最终形式化结果是一个复杂而美丽的结构。图 2 展示了这个“近乎 5 染色”。红色区域代表未染色的“垃圾”区域。

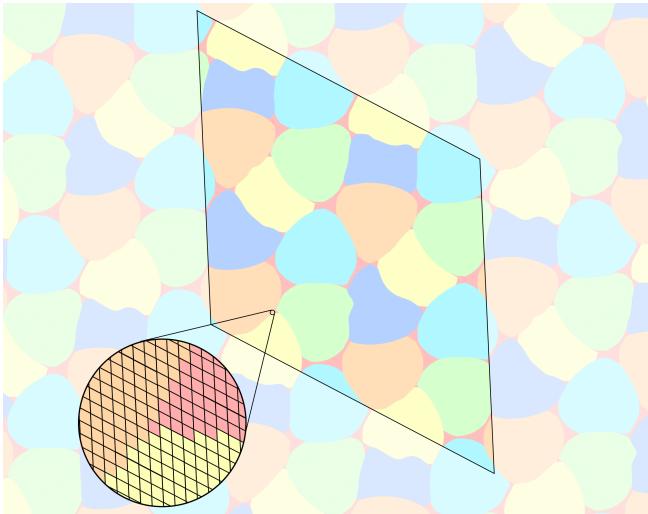
带有红色未染色区域的形式化近乎 5 染色。

注意下方左侧对比图 (图 5) 中的“波状”边界。网络经常产生有机的、流动的形状，因为解空间中存在自由度。

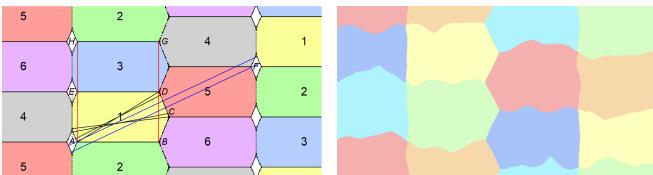
Pritikin/Parts 染色与神经网络波状染色的对比。

案例研究 2: 非对角的发现

该论文最重要的理论贡献涉及一个称为 “非对角 (Off-Diagonal) ”哈德维格-纳尔逊问题 的变体。

在标准问题中，每种颜色都必须避免距离 1。在非对角版本中，不同的颜色避免不同的距离。类型为 \((d_1, d_2, \dots, d_k)\) 的染色意味着颜色 1 避免距离 \(d_1\)，颜色 2 避免距离 \(d_2\)，依此类推。

研究人员寻找类型为 \((1, 1, 1, 1, 1, d)\) 的 6 染色。这意味着 5 种颜色避免单位距离，而第 6 种颜色避免某个距离 \(d\)。

扩展连续统

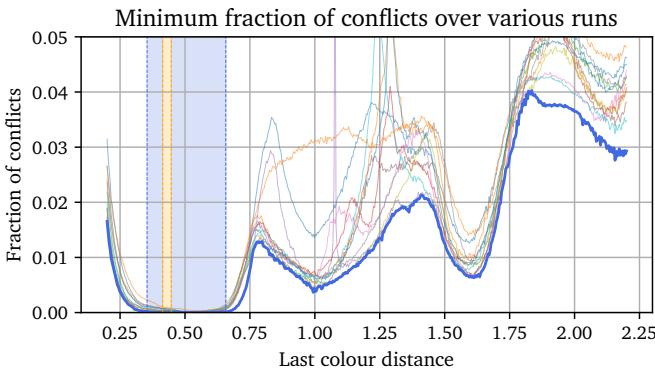
30 多年来，这种染色存在的有效距离 \(d\) 的范围一直停留在特定区间内。研究人员训练他们的网络扫描不同的 \(d\) 值，寻找损失函数降至零的区域。

为了高效地做到这一点，他们将距离 \(d\) 与坐标一起作为 输入 喂给神经网络。这使得单个网络可以一次性学习整个距离连续统的解。

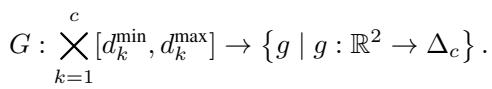
以距离为输入的染色算子定义。

结果是突破性的。他们发现了两种新的、截然不同的 6 染色方案。

第一种染色 (可变 \(d\)) : 他们发现了一族适用于 \(0.354 \leq d \leq 0.553\) 的染色。下图 (图 6) 绘制了冲突率与距离 \(d\) 的关系。蓝色阴影区域代表 AI 发现的 新 解范围，显著扩展了先前已知的橙色区域。

显示新扩展范围内冲突减少的图表。

第二种染色 (固定范围) : 他们还发现了一种特定的模式，适用于 0.418 到 0.657 之间的任何 \(d\)。

这正是“视觉发现”大放异彩的地方。图 1 左侧显示了神经网络的原始输出。它看起来像一扇嘈杂的、柔和的彩色玻璃窗。右侧是通过解释该噪声得出的人类形式化构造。

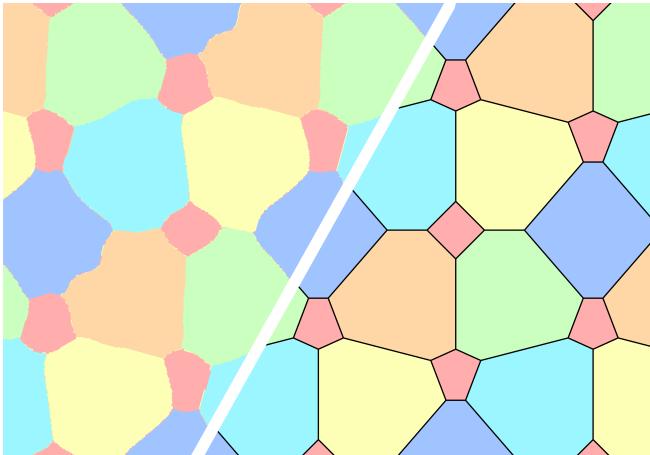
神经网络输出与形式化染色的并排对比。

形式化版本 (下图 图 11) 展示了巧妙的多边形镶嵌。红色 (颜色 6) 被精心放置以避免特定的距离范围，而其他颜色处理单位距离。

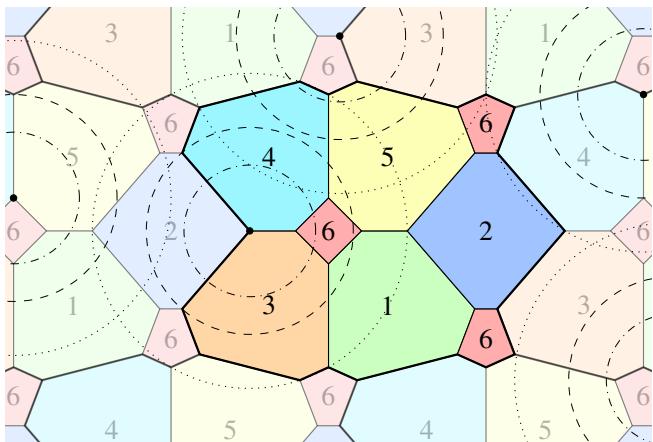
新颖的 6 染色构造的详细图解。

图 3 可视化了特定实例 (\(d=0.45\)) 的约束。红点的间隔使得它们永远不会落在虚线圆 (半径 0.45) 上。

红点避免距离 0.45 的形式化染色。

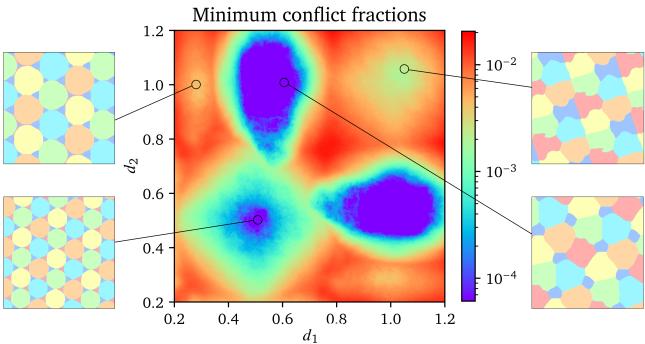
他们还探索了 两种 颜色具有非单位距离 \((1, 1, 1, 1, d_1, d_2)\) 的染色。通过在热图 (图 7) 上绘制冲突极小值，他们确定了稳定性岛屿——即可能存在有效染色的区域。这对数学家来说就像一张藏宝图，指引他们确切地去哪里寻找证明。

两个可变距离的冲突比例热图。

案例研究 3: 避免单色三角形

HN 问题处理的是点对。一个更难的变体问道: 需要多少种颜色来避免特定边长的单色三角形？

具体来说，我们能否为平面染色，使得没有三个构成边长为 \((1, a, b)\) 三角形的点是同一种颜色的？

为了解决这个问题，作者修改了损失函数以观察点的三元组。

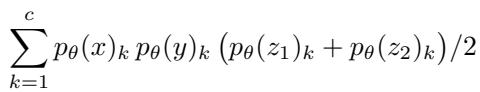
针对三角形三元组修改的损失函数。

在这里，\(z_1\) 和 \(z_2\) 是与点 \(x\) 和 \(y\) 构成特定三角形的点。

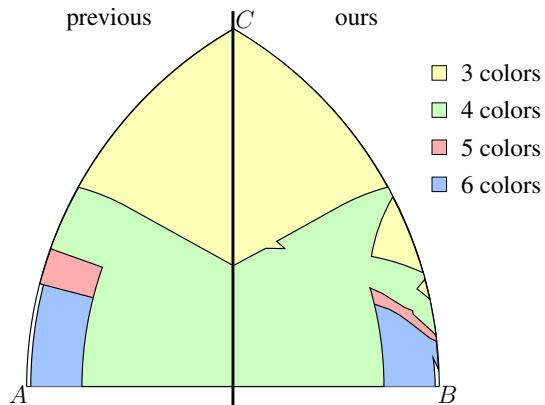
结果对已知界限进行了大幅更新。在下面的图 4 中，左侧图表显示了“之前 (Previous) ”的知识状态。彩色区域代表可以用 3、4、5 或 6 种颜色解决的三角形尺寸 \((a, b)\)。右侧图表显示了“我们 (Ours) ”的结果。

注意 3 色和 4 色 (黄色和绿色) 的区域是如何显著扩大的。AI 发现了人类未针对这些特定三角形形状进行优化的基于条纹的图案和六边形镶嵌。

单色三角形参数空间的比较。

探索更高维度

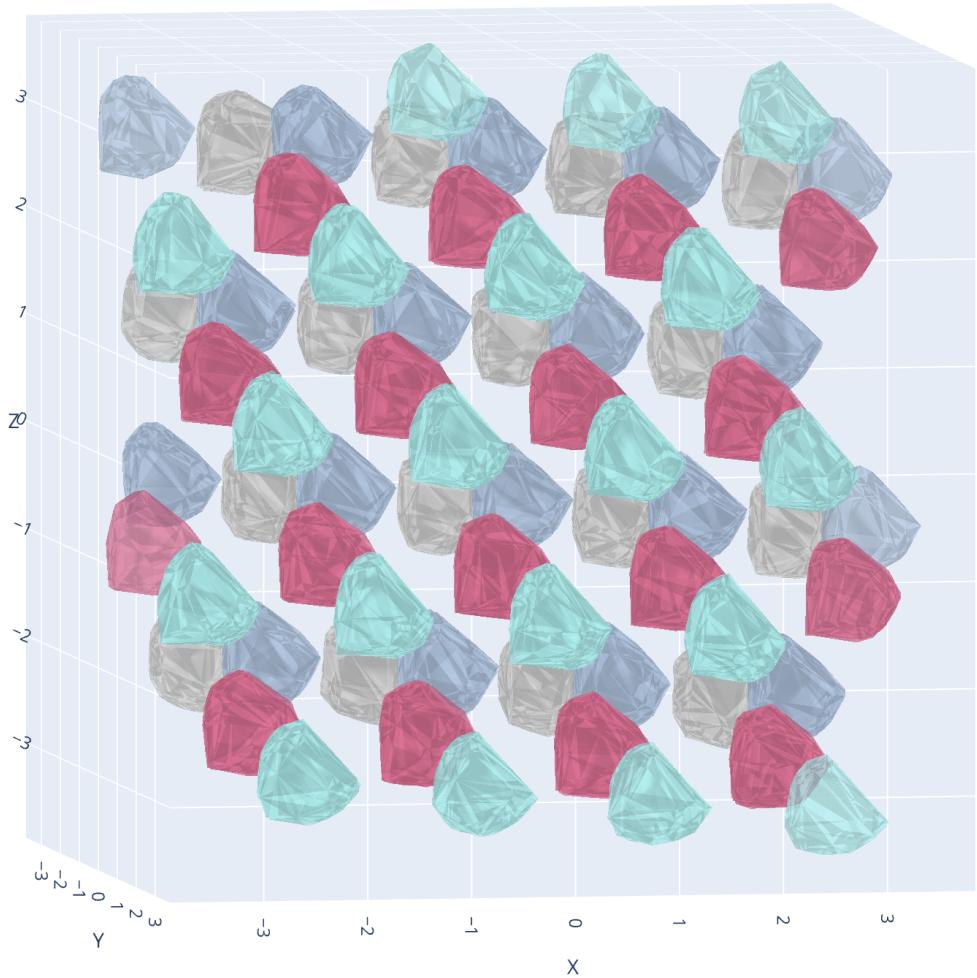
最后，作者将他们的框架带入了 3D 空间 (\(\mathbb{R}^3\)) 。已知“空间的色数”最多为 15。作者的方法成功找到了无冲突的 15 染色。

可视化 3D 染色很困难，但神经网络可以毫不费力地处理额外的维度——这只是另一个输入节点而已。图 15 展示了发现的 3D 染色的一个切片，揭示了类似宝石的多面体结构。

显示宝石结构的 3D 染色可视化。

结论: 数学中 AI 的未来

论文“数学中的神经发现”是对 AI for Science (AI 助力科学) 范式的有力证明。它并没有取代数学家；相反，它增强了他们的能力。

这里建立的工作流程非常强大:

  1. 重述 : 将离散问题转化为可微的损失函数。
  2. 训练 : 训练神经网络找到近似解 (“做梦”阶段) 。
  3. 解释 : 解释视觉模式以推导形式化的数学构造。
  4. 验证 : 使用严密的逻辑验证构造。

作者利用这一点改进了哈德维格-纳尔逊问题的界限，而这些界限已经存在了数十年。神经网络不仅仅是在处理数字；它们充当了显微镜，揭示了连续统中以前人类直觉无法看见的几何结构。随着这些技术的完善，我们可能会发现机器不仅会梦见彩色平面——它们可能会构想出未来的定理。