引言

科学和数据分析中最根本的挑战之一就是区分相关性和因果性。虽然机器学习模型擅长发现模式 (相关性) ，但它们往往难以告诉我们事情发生的原因 (因果性) 。为了弥补这一差距，研究人员依靠有向无环图 (DAGs) 来描绘变量之间的因果关系。

然而，这里有个陷阱。在许多现实场景中，观测数据不足以确定一个唯一的因果图。相反，我们会得到一组同样符合数据的可能图集。这个集合被称为马尔可夫等价类 (Markov Equivalence Class, MEC) 。

了解这个类的大小——即数据有多少种可能的因果解释——至关重要。它告诉我们还存在多少不确定性，并帮助研究人员设计下一组实验以缩小真相范围。但这存在一个计算瓶颈: 计算这些图的数量非常困难。随着变量数量的增加，可能的 DAG 数量呈超指数级爆炸式增长。

2023 年，一种名为团选择 (Clique-Picking, CP) 算法的方法通过允许在多项式时间内对特定类型的图进行计数，取得了突破。但即使是该方法也存在效率低下的问题，经常进行不必要的重复计算。

在这篇文章中，我们将深入探讨 Liu、He 和 Guo 在 2025 年发表的研究论文: “An Improved Clique-Picking Algorithm for Counting Markov Equivalent DAGs via Super Cliques Transfer” (通过超团转移改进的计算马尔可夫等价 DAG 的团选择算法) 。这项工作引入了一种称为“超团转移”的巧妙优化，通过识别图结构可以被“回收利用”而不是从头重建，从而大幅加快了计数过程。

背景: 因果计数问题

在剖析新算法之前，我们需要了解因果发现的背景以及研究人员正在解决的具体问题。

马尔可夫等价类 (MEC) 和 CPDAGs

当我们无法识别唯一的因果 DAG 时，我们使用一个称为完全部分有向无环图 (CPDAG) (或本质图) 的图来表示整个等价 DAG 类。

在 CPDAG 中:

  • 有向边 (\(A \rightarrow B\)) 表示在类中所有图中都固定的因果关系。每个人都同意 \(A\) 导致 \(B\)。
  • 无向边 (\(A - B\)) 表示不确定性。在某些有效图中，\(A\) 导致 \(B\)；在其他图中，\(B\) 导致 \(A\)。

目标是在不产生环或新的条件独立性 (v-结构) 的情况下，计算有多少种方法可以将这些无向边解析为有向边。

分解策略

如果我们可以将图分解，计数问题就会简化。CPDAG 的无向部分形成了无向连通分量 (UCCGs) 。 这些分量是弦图 (任何长度为 4 或更长的环都有捷径的图) 。

有效 DAG 的总数是这些分量大小的乘积。

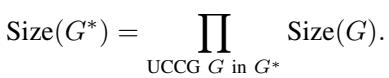
根据分量计算 MEC 大小的公式。

这里，\(Size(G^*)\) 是总数，我们将各个分量 (\(G\)) 的计数相乘。因此，挑战在于高效地计算每个 UCCG 的有效方向。

团选择 (CP) 算法

这就是 2023 年“团选择”算法发挥作用的地方。它利用了一种称为团树 (Clique Tree) 的结构。弦图可以被看作一棵树，其中每个节点是一个极大团 (一个全连接的子图) 。

CP 算法递归地工作:

  1. 它选择一个团作为根。
  2. 它将边从该根向外定向。
  3. 此操作将图分解为更小的未连接分量。
  4. 它解决这些小块的问题。

虽然与指数级搜索相比效率很高，但 CP 算法有一个缺陷。为了获得正确的计数，它必须遍历充当根的每一个可能的极大团。

对于一个具有 \(m\) 个团、顶点 \(V\) 和边 \(E\) 的图，为单个根生成子问题的成本大致与图的大小成正比。由于 CP 算法对每个团都执行此操作，因此复杂度达到 \(\mathcal{O}(m(|V| + |E|))\)。

新论文的洞见: 当你将树的根从团 A 移动到团 B 时，图的绝大部分结构并没有改变。以前的算法在每一步都盲目地重建整个世界。新算法, 超团转移 (Super Cliques Transfer) , 保留了共享结构，只更新必要的部分。

核心方法: 超团与转移

作者提出了一种将复杂度降低到 \(\mathcal{O}(m^2)\) 的方法。这是一个显著的改进，特别是对于边数 \(|E|\) 非常大的稠密图。

为了理解他们是如何实现这一点的，我们需要定义三个概念: 团树、超团和转移操作 。

1. 有根团树

让我们可视化这个数据结构。下图 1(a) 显示了一个图 (UCCG)。图 1(c) 显示了它的团树 。

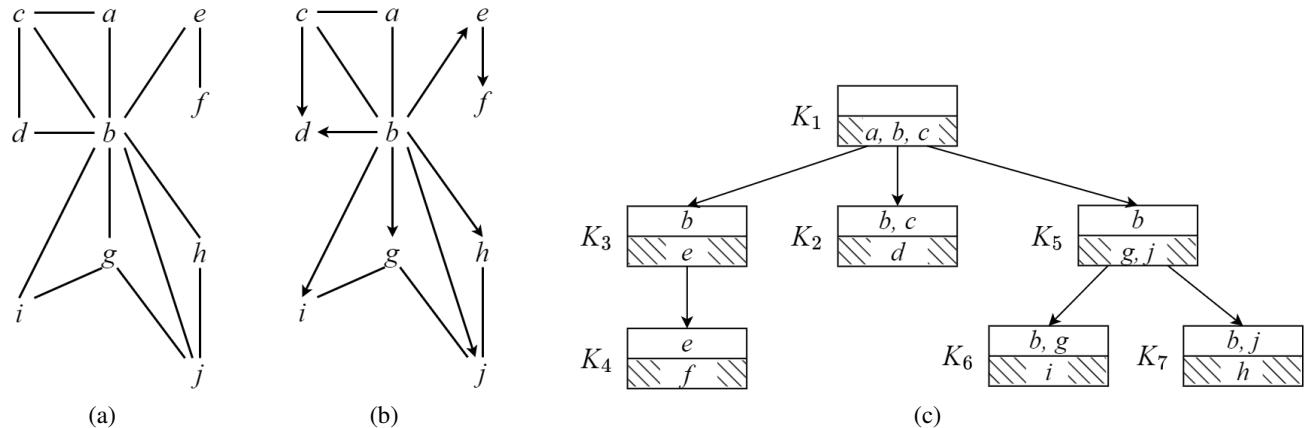
(a) 一个无向图。(b) 以 K1 为根定向的图。(c) 显示极大团之间关系的团树结构。

在图 1(c) 中，树以团 \(K_1 = \{a, b, c\}\) 为根。

  • \(K_1\) 是父节点。
  • \(K_2, K_3, K_5\) 是子节点。
  • 团之间的交集 (例如 \(K_1\) 和 \(K_2\) 之间的 \(\{b, c\}\)) 称为分离集 (separators) 。
  • 团的独特部分 (例如 \(K_2\) 中的 \(\{d\}\)，它不在 \(K_1\) 中) 称为残差集 (residuals) 。

当 \(K_1\) 被选为根时，它强制对图进行定向 (图 1b) 。剩下的无向部分 (如 \(g\) 和 \(j\) 之间的边) 是我们需要解决的子问题。

2. 引入“超团”

作者观察到，当你遍历团树时，某些团组作为一个单元行动。他们将这些单元定义为超团 (Super Cliques) 。

一个超团由一个“团头”及其“团尾”组成。

  • 团头 (Clique Header): 一个团，其分离集不是其父节点分离集的子集。它代表结构上的“断裂”或新分支。
  • 团尾 (Clique Tail): 一个后代团，其分离集是团头分离集的真子集。它本质上“跟随”着团头。

这种分组为什么重要？因为超团内的残差集 (独特的顶点) 形成了我们试图计数的具体无向分量。

作者正式定义超残差 (\(\mathrm{SR}\)) 为属于一个超团的残差集的集合:

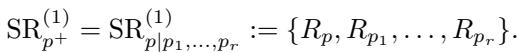
超残差的定义，包含团头及其尾部的残差。

这引出了一个强大的定理。有根树的无向连通分量集 (\(\mathcal{C}_G(K_1)\)) 本质上只是由这些超残差导出的图的集合。

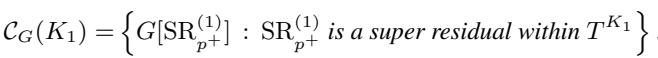
定理说明分量集对应于由超残差导出的图。

简而言之: 如果你能识别树中的超团，你就立即识别了你需要计数的子问题。 你不需要每次都对图顶点运行复杂的搜索算法。

3. 转移操作 (“魔法”步骤)

这是核心创新点。假设我们已经计算了以 \(K_1\) 为根的树的超团。现在我们想知道如果将树的根设为 \(K_5\) 会有什么结果。

在标准方法中，我们会从头开始重建树。而在这种方法中，我们执行转移 。

当我们把根从父节点 \(K_1\) 移动到子节点 \(K_i\) (例如 \(K_5\)) 时，只有它们之间的边反转方向 (\(K_1 \rightarrow K_5\) 变为 \(K_5 \rightarrow K_1\)) 。

  • \(K_5\) 成为新的全局根。
  • \(K_1\) 成为 \(K_5\) 的子节点。
  • 树的其余结构 (\(K_5\) 的兄弟节点，\(K_5\) 的后代) 基本保持不变，尽管它们作为头或尾的状态可能会发生局部变化。

作者提供了一个查找表 (表 1) ，确定了在这个单一的边翻转过程中, 分离集和残差集究竟如何变化。

比较两种树配置下的分离集和残差集的表格。

注意更新是多么简单。对于大多数团，分离集和残差集根本不变。只有参与交换的两个团 (\(K_1\) 和 \(K_i\)) 看到了它们内部集合的更新。

可视化变化

让我们看一个结构变化的具体例子。图 2 显示了从以 \(K_1\) 为根的树 (左) 到以 \(K_5\) 为根的树 (右) 的过渡。

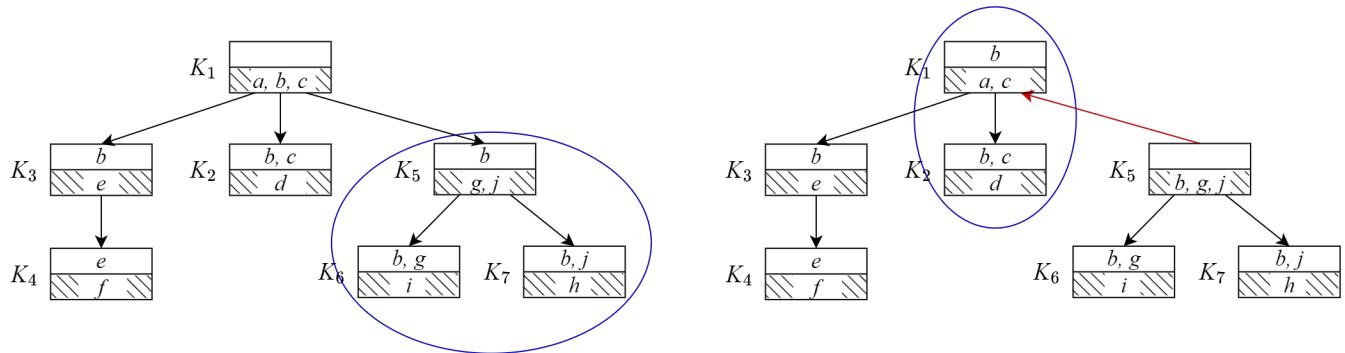
以 K1 与 K5 为根时树结构的比较，展示了超团分组。

在左侧 (\(T^{K_1}\)):

  • \(K_5\) 是 \(K_1\) 的子节点。
  • \(K_5\) 有尾部 \(K_6\) 和 \(K_7\)。
  • 它们形成一个超团 (蓝色圆圈) : \(\{K_5, K_6, K_7\}\)。

在右侧 (\(T^{K_5}\)):

  • 我们让 \(K_5\) 成为根。
  • 与 \(K_6\) 和 \(K_7\) 的关系破裂；\(K_6\) 和 \(K_7\) 成为它们自己独立的超团，因为 \(K_5\) 现在是“老板” (根) ，不再以同样的方式充当它们的头。
  • 然而，看看 \(K_1\)。它现在是 \(K_5\) 的子节点。
  • \(K_2\) 原本是 \(K_1\) 的子节点。它跟随 \(K_1\) 进入新结构。
  • 它们形成一个新的超团: \(\{K_1, K_2\}\)。

该算法 SC-Trans 将此逻辑机械化。它根据分离集简单的子集关系，识别哪些超团分裂开来，哪些合并在一起。

新根的更新后的超残差通常采用这种形式，将旧根的残差与特定的尾部合并:

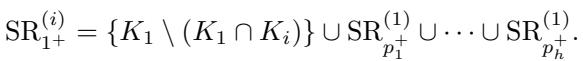
转移后新超残差的公式。

算法工作流

研究人员将此逻辑实现为一个迭代算法。

  1. 初始化: 为第一个团 \(K_1\) 构建团树。找到它的超团。
  2. 迭代: 移动到相邻的团 \(K_2\)。
  3. 转移: 使用上述逻辑即时更新超团和残差，无需触及底层图顶点。
  4. 重复: 遍历整棵树，直到每个团都充当过根。

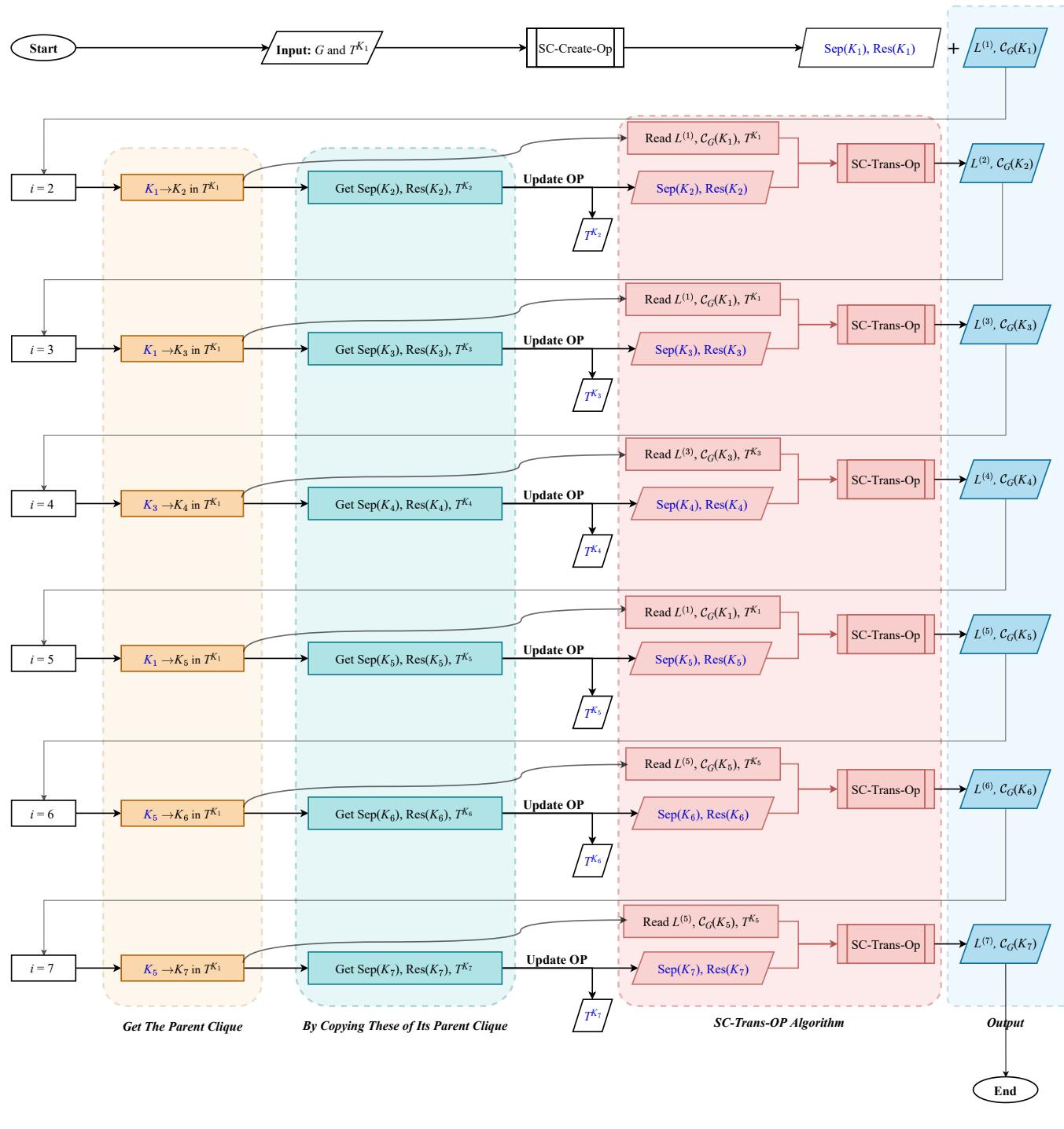
SC-Trans 算法的分步流程图。

这个工作流本质上是一步步地“变形”树结构，将计算结果 (\(\mathcal{C}_G\)) 从邻居传递给邻居。

实验与结果

这种理论上的结构“回收”真的节省时间吗？作者将他们的改进团选择 (ICP) 算法与标准的团选择 (CP) 算法进行了比较。

他们在具有不同顶点数 (\(V\)) 和图密度 (\(r\)) 的弦图上进行了测试。

顶点数量的性能

在图 3(a) 和 3(b) 中，我们可以看到随着顶点数量的增加，运行时间 (对数刻度) 的变化。

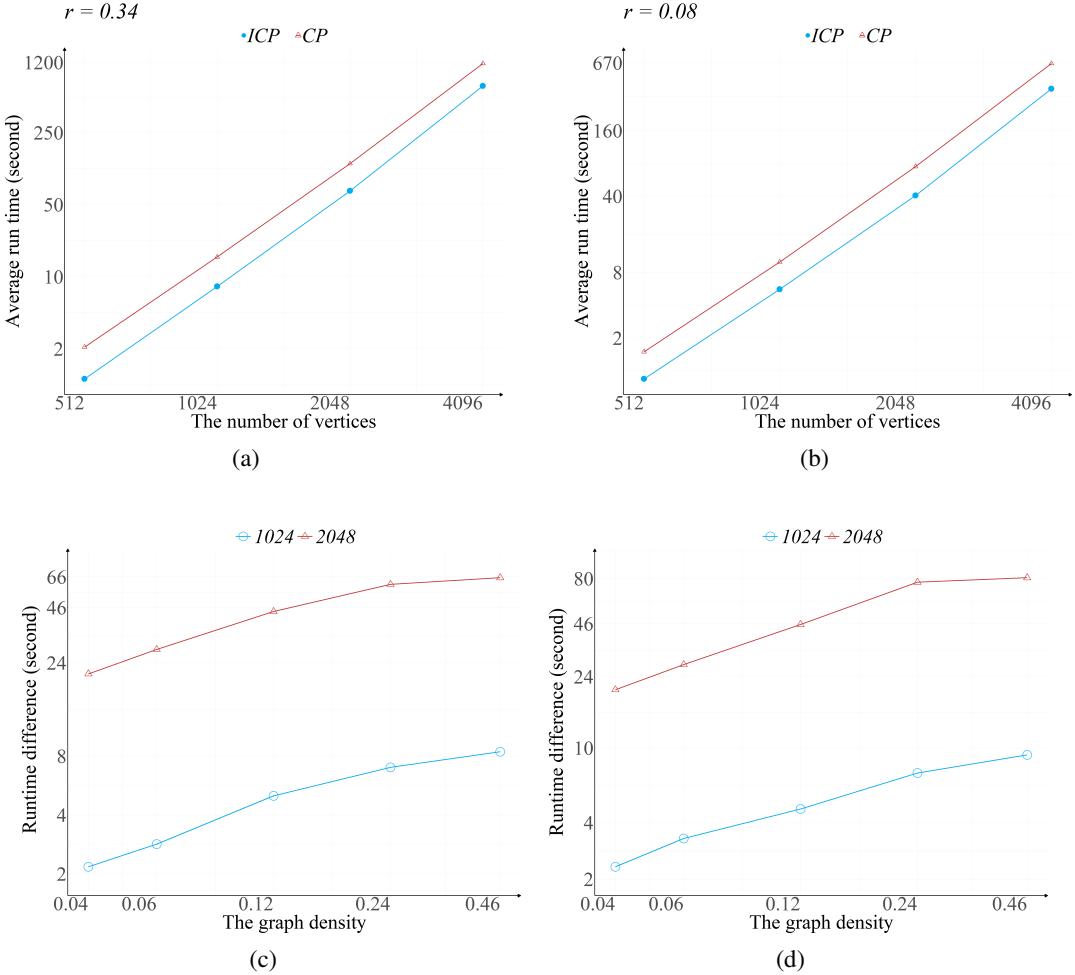
显示 CP 和 ICP 算法之间运行时间比较的图表。

  • 蓝线 (ICP): 新方法。
  • 橙线 (CP): 标准方法。

新方法始终更快。请注意，两个轴都是对数的；这里明显的差距代表了显著的倍数级加速。

密度的影响

图的“密度”原来是一个主要因素。下表比较了随着密度 (\(r\)) 增加，运行时间的差异。

表 3 比较了不同图密度下的运行时间差异。

列 \(T_{CP, 2} / T_{ICP, 2}\) (分量生成步骤的运行时间比率) 特别说明问题。

  • 在低密度 (\(r=0.04\)) 下，新方法快约 5 倍 。
  • 在高密度 (\(r=0.46\)) 下，新方法快约 153 倍到 264 倍 。

为什么？在稠密图中，团的数量 (\(m\)) 很大，但与边相比，顶点的数量 (\(V\)) 可能相对较小。旧算法的复杂度依赖于 \(|V| + |E|\)，这在稠密图中会爆炸。新算法依赖于 \(m^2\)。通过在每一步中消除对顶点/边遍历的依赖，ICP 方法在处理复杂的、相互关联的因果结构方面变得极其优越。

结论与启示

“超团转移”算法代表了图因果分析的一次巧妙进化。通过将视角从处理原始图顶点转移到操作高层树结构 (超团) ，作者成功消除了先前最先进方法中的主要冗余。

关键要点:

  1. 不要重新计算: 在团树中，改变根会显著影响局部结构，但使全局结构基本保持完整。
  2. 超团: 识别这些稳定的团组可以高效地跟踪图分量。
  3. 效率: 该方法将复杂度降低到 \(\mathcal{O}(m^2)\)，使其在稠密图上具有高度的可扩展性。

对于因果推理的学生和研究人员来说，这项工作提醒我们数据结构的重要性。计算马尔可夫等价 DAG 的问题在数学上很繁重，但解决方案来自经典的计算机科学原则: 增量更新总是比完全重新计算更便宜。随着我们继续将因果发现应用于更大、更复杂的数据集 (如基因网络或经济模型) ，像这样的优化将成为使分析变得可行的引擎。