引言

想象一下你正在尝试学习一门复杂的新学科，比如微积分或一门新语言。如果你试图在学习基础知识的同时立即攻克最难的概念，你很可能会感到不知所措并最终失败。相反，人类通过“课程 (curriculum) ”学习的效果最好: 我们先掌握简单的概念，建立信心和理解，然后再去解决难题。

在 AI 科学计算领域，特别是物理信息神经网络 (PINNs) 中，模型通常没有这种奢侈的待遇。它们通常被迫同时学习所有内容——包括简单的平滑区域和复杂的混沌边界。这往往导致模型在关键区域失效。

一篇题为 “CoPINN: Cognitive Physics-Informed Neural Networks” 的新研究论文提出了一个极具吸引力的解决方案。通过模仿人类“由易到难”的认知过程，研究人员创建了一个框架，大幅提高了求解偏微分方程 (PDEs) 的准确性。

在这篇文章中，我们将剖析 CoPINN 的工作原理，为什么传统方法在处理“顽固”数据点时会遇到困难，以及这种新的认知方法如何实现最先进的结果。

问题所在: 不平衡预测

偏微分方程 (PDEs) 是宇宙的数学语言。它们描述了热扩散、流体动力学、波的传播以及量子力学。准确求解它们对于工程和科学至关重要。

物理信息神经网络 (PINNs) 已成为解决此类问题的一种强有力的工具。PINN 不使用网格 (像传统的数值方法那样) ，而是使用神经网络来逼近解，并利用物理定律 (PDE 本身) 作为损失函数中的约束条件。

“顽固”区域

然而，标准 PINN 有一个主要缺陷: 它们平等地对待模拟空间中的每一个点。

实际上，物理问题的解很少是均匀的。有些是“简单”区域，解的变化缓慢；有些是“困难”区域——通常在边界或激波附近——数值变化非常剧烈。当神经网络试图同时最小化所有点的平均误差时，它倾向于优先拟合简单、平滑的区域，因为它们更容易拟合。这就导致了 不平衡预测问题 (Unbalanced Prediction Problem, UPP) 。

模型本质上陷入了一个“懒惰”的局部极小值。它能得到大致的形状，但在复杂的边界处却遭遇灾难性的失败。

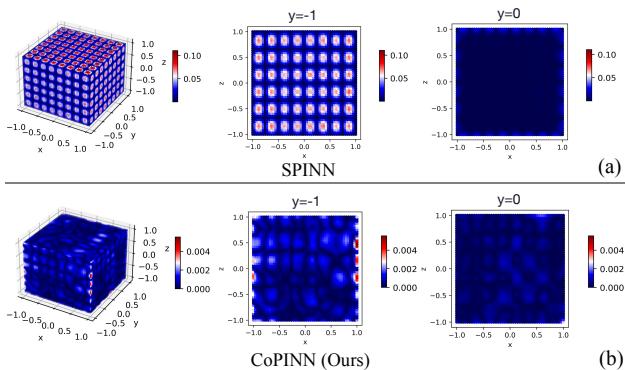
Figure 1. The 2D and 3D visualization of the absolute error between the predicted and exact values. Comparison between SPINN and CoPINN.

如上图 Figure 1 所示，一种名为 SPINN (部分 a) 的最先进方法在物理边界 (\(y = -1\)) 附近表现出巨大的误差 (红点) 。相比之下，本文提出的 CoPINN (部分 b) 在整个域内 (包括困难的边界) 都保持了一致的低误差率。

CoPINN 的解决方案

为了解决 UPP，研究人员推出了 CoPINN 。 该框架整合了三个关键创新:

  1. 可分离学习 (Separable Learning) : 用于高效处理高维数据。
  2. 难度评估 (Difficulty Evaluation) : 一种让网络自我评估问题哪些部分“困难”的方法。
  3. 认知训练调度器 (Cognitive Training Scheduler) : 一种引导学习过程从易到难的机制。

让我们看看整体框架:

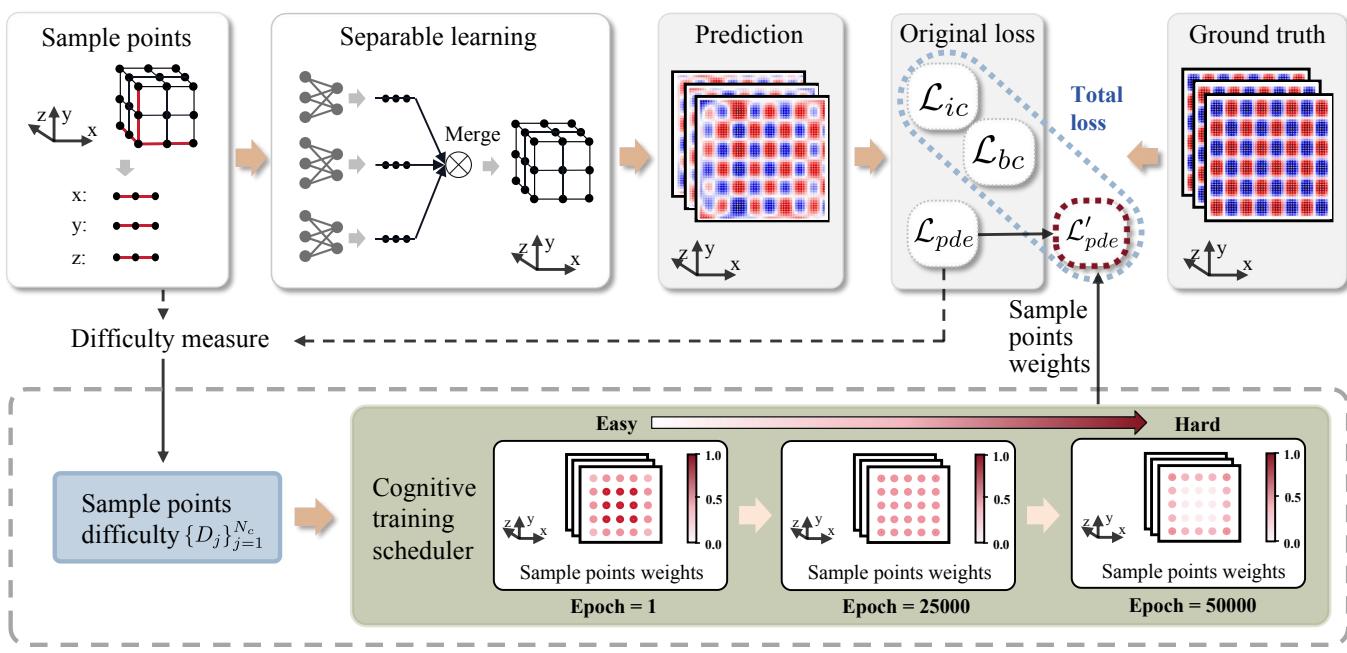
Figure 2. The frameworks of CoPINN. Separable sub-networks encode independent coordinates, followed by aggregation and a cognitive training scheduler.

1. 可分离学习架构

在探讨“认知”层面之前，作者首先解决了计算成本问题。标准 PINN 使用单个多层感知机 (MLP) ，将所有坐标 \((x, y, z, t)\) 作为输入。随着维度的增加，这在计算上变得非常昂贵。

CoPINN 采用了 可分离架构 。 它不使用一个巨大的网络，而是为每个坐标轴使用独立的子网络。

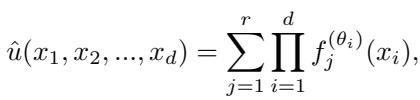
Equation describing the separable prediction function.

如上式所示，预测值 \(\hat{u}\) 是通过乘积和的形式聚合这些较小网络的输出而构建的。这使得模型能够高效地处理输入坐标矩阵，显著减少了高维 PDE 的内存使用和训练时间。

2. 衡量难度

CoPINN 的核心在于区分“简单”和“困难”样本的能力。但是神经网络如何知道什么是困难的呢？

研究人员提出使用 PDE 残差的梯度 作为难度的代理指标。

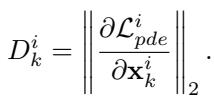
Equation for measuring difficulty based on PDE residual gradients.

这里，\(D_k^i\) 代表第 \(k\) 个样本在第 \(i\) 个 epoch 的难度。

  • 低梯度: 物理损失稳定；该区域可能是平滑的。 (简单)
  • 高梯度: 物理损失变化迅速；这表明该区域存在剧烈转变或复杂边界。 (困难)

通过计算这个动态难度分数，模型可以识别出通常导致标准 PINN 失败的“顽固”区域。

3. 认知训练调度器

这就是“类人”学习发生的地方。作者提出了一个受 自步学习 (Self-Paced Learning, SPL) 启发的调度器。

目标是优化损失函数，其中包括 PDE 约束项 (\(\mathcal{L}_{pde}\))、初始条件项 (\(\mathcal{L}_{ic}\)) 和边界条件项 (\(\mathcal{L}_{bc}\))。

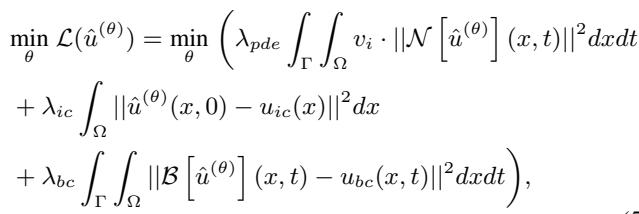
Equation showing the weighted loss function minimization.

注意上式中的 \(v_i\) 项。这是分配给每个样本的动态权重。 认知训练调度器 根据样本的难度 (\(D\)) 随时间调整这些权重 (\(v_i\)) 。

课程策略

训练过程根据 epoch 分为几个阶段:

  1. 早期训练 (热身) : 模型为 简单 样本分配较高的权重 (\(v_e\))，为 困难 样本分配较低的权重 (\(v_h\))。网络建立起对解的总体结构的基本理解。
  2. 中期训练: 权重趋于平衡。
  3. 后期训练: 重心转移。模型为 困难 样本分配更高的权重，迫使网络去优化它之前忽略的顽固边界区域的预测。

这些权重的演变由超参数 \(\beta\) 和当前的 epoch 数决定。

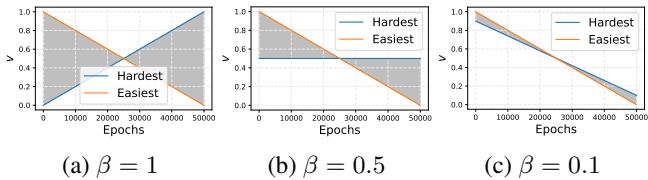
Figure 3. Different beta values in cognitive training scheduler result in a range of changes in weight v.

Figure 3 展示了这种转变。

  • 橙色线 (最简单的样本) 以高权重 (1.0) 开始，随时间下降。
  • 蓝色线 (最难的样本) 以 0 权重开始并上升。
  • 取决于 \(\beta\) 值 (一个超参数) ，交叉点会发生变化。作者发现，逐渐的转变 (如图 c 所示) 通常能防止模型遗忘之前学到的内容。

计算第 \(i\) 个 epoch 中特定样本 \(j\) 的权重的具体公式结合了全局的简单/困难趋势以及该样本的具体难度:

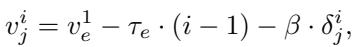
Equation for calculating the weight of a specific sample j at epoch i.

这种动态调整确保模型不会因为过早尝试学习复杂边界而陷入局部极小值。

实验与结果

为了验证 CoPINN，研究人员将其与七个最先进的基准模型 (包括常规 PINN、SPINN 和 Region-Optimized PINN) 在具有挑战性的物理方程上进行了对比测试:

  • 亥姆霍兹方程 (Helmholtz Equation)
  • 扩散方程 (Diffusion Equation)
  • 克莱因-戈尔登方程 (Klein-Gordon Equation, \((2+1)d\) 和 \((3+1)d\))
  • 流体混合问题 (Flow Mixing Problem)

定量优势

结果在统计上非常显著。以下是亥姆霍兹、克莱因-戈尔登和扩散方程的数据表。

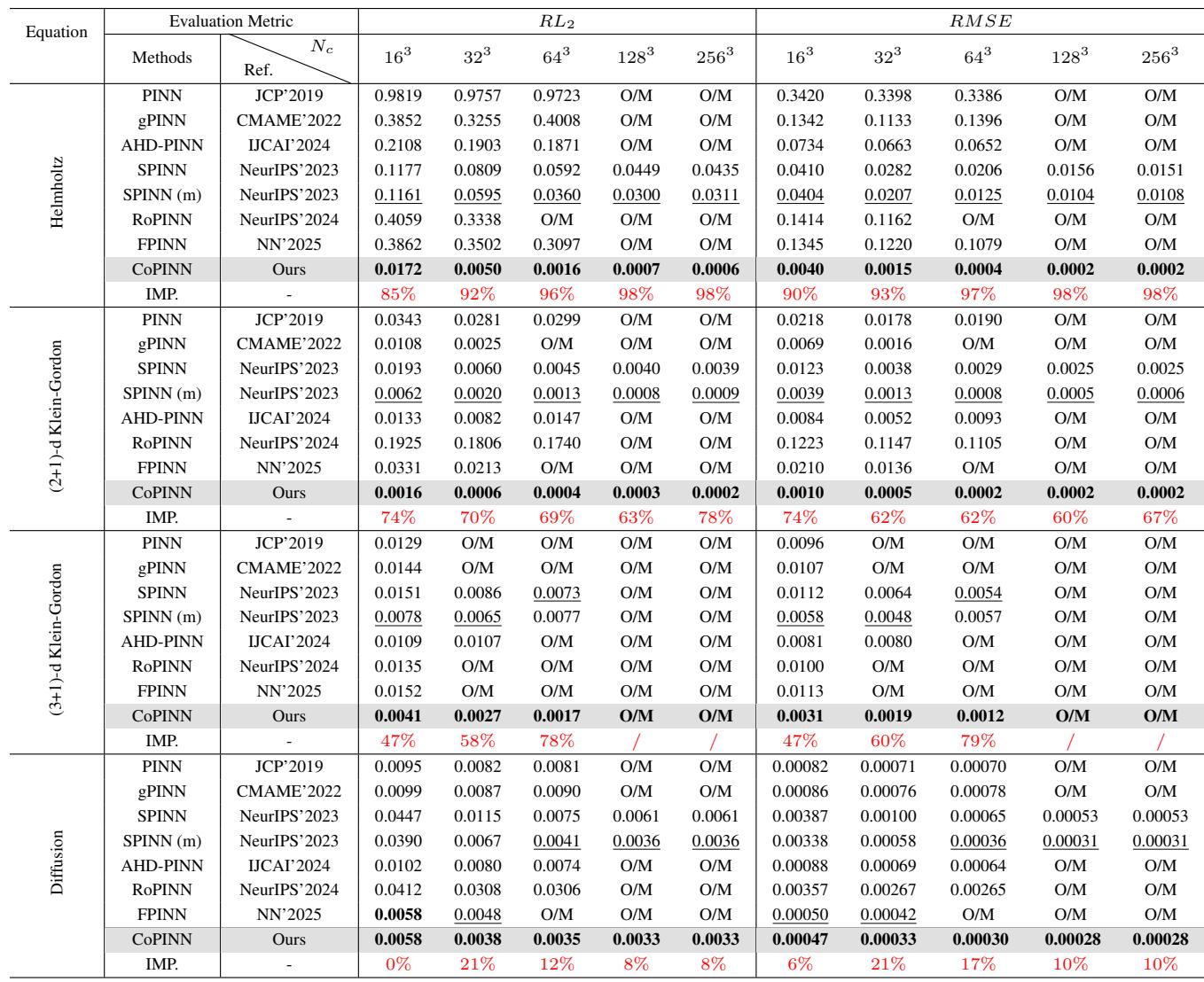
Table 1. Full results of the Helmholtz, (2+1)-d Klein-Gordon and Diffusion equation.

数据的主要结论:

  • 亥姆霍兹方程: 由于其波动的性质，这是一个特别难解的方程。在 \(256^3\) 个配点 (collocation points) 下，CoPINN 实现了 0.0006 的相对 L2 误差 (\(RL_2\)) 。排名第二的方法 (SPINN-m) 得分为 0.0311。这是精度的巨大提升。
  • 一致性: CoPINN 在几乎所有数据集和分辨率下都取得了最佳性能。
  • 可扩展性: 虽然许多方法在高分辨率 (\(128^3\) 和 \(256^3\)) 下因内存不足 (O/M) 而运行失败，但 CoPINN 的可分离架构使其能够成功训练。

可视化分析

数字固然重要，但可视化流场能展示改进发生的具体位置。

下方的 Figure 4 展示了亥姆霍兹数据集上的对比。请仔细观察“绝对误差 (Absolute Error) ”一栏。

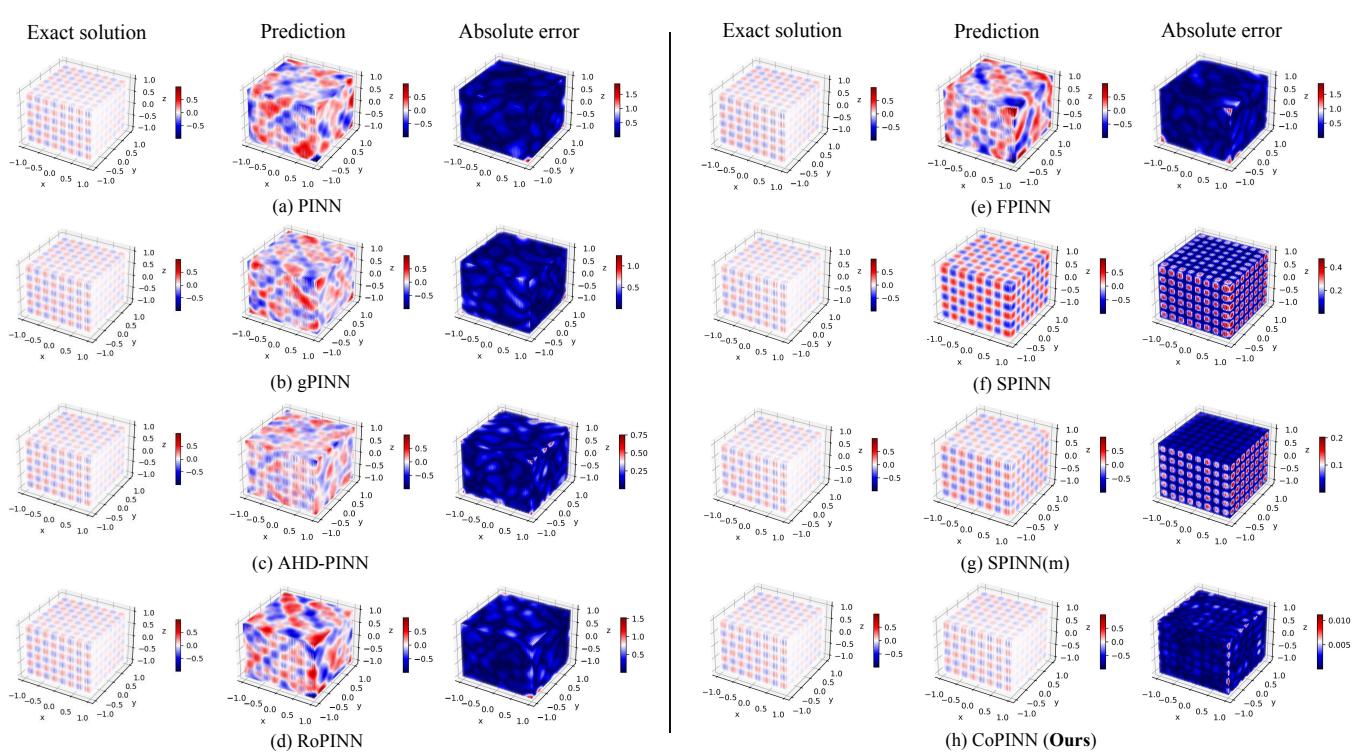
Figure 4. Prediction results of CoPINN and the seven baselines on the Helmholtz dataset.

  • 行 (a) PINN: 误差图呈鲜艳的红/蓝色，表明与精确解有巨大偏差。
  • 行 (f) SPINN: 好一些，但仍显示出显著的误差结构。
  • 行 (h) CoPINN: 误差图几乎是空白的 (深蓝色) ，表明预测结果与精确解几乎完全一致。

我们在 (2+1)-d 克莱因-戈尔登 数据集上也看到了类似的结果:

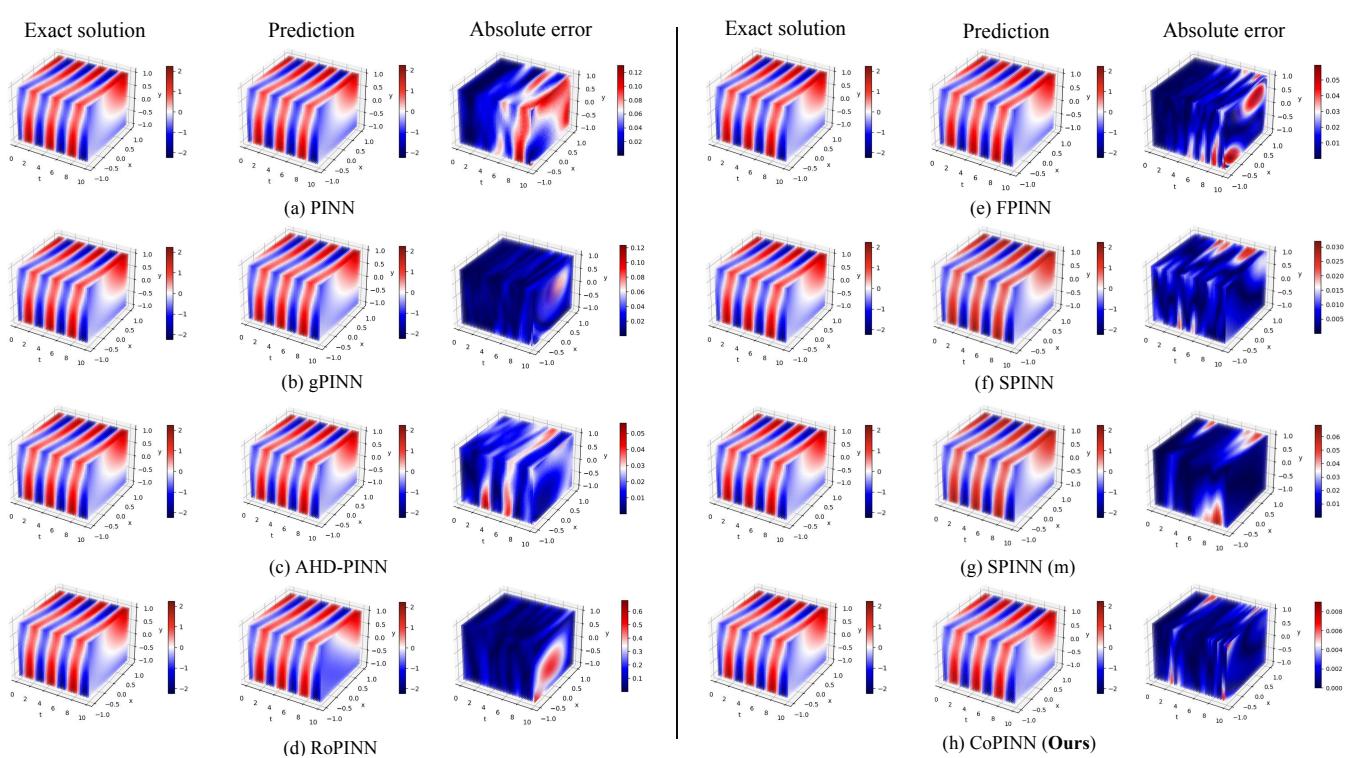
Figure 5. Prediction results on the (2+1)-d Klein-Gordon dataset.

同样，CoPINN (行 h) 有效地消除了困扰其他方法的误差 (如行 b 中的 gPINN) ，特别是在解发生震荡的区域稳定了学习过程。

收敛稳定性

人们可能会担心动态改变样本权重会导致训练不稳定。然而，误差分析显示情况恰恰相反。

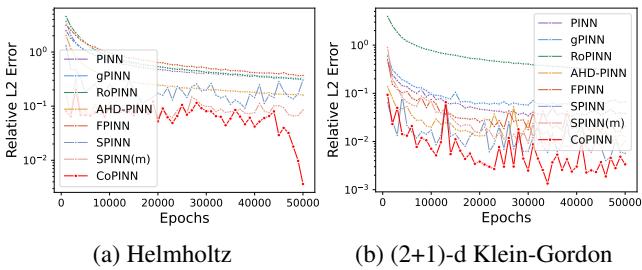
Figure 7. Variation curve of Relative L2 Error with the increase of epoch.

在 Figure 7 中，CoPINN 的误差曲线 (红色) 呈现可靠的下降趋势。虽然随着权重的变化会有微小的波动 (这在课程学习中是预期的) ，但最终的收敛点显著低于所有竞争对手。

结论

“不平衡预测问题”长期以来一直是物理信息神经网络准确性的隐形杀手。通过对复杂的边界湍流和平滑的内部流动一视同仁，传统模型往往在精度最关键的地方失效。

CoPINN 成功解决了这个问题，它借鉴了人类教学法: 先爬后走，先走后跑。

通过将高效的可分离架构与智能提升难度的认知调度器相结合，CoPINN 实现了:

  1. 更高的精度: 在某些情况下将误差降低了几个数量级。
  2. 鲁棒性: 正确求解顽固的边界区域。
  3. 效率: 在不耗尽内存的情况下处理高分辨率的 3D 和 4D 问题。

这项研究强调，在深度学习中，模型如何学习与它学习什么同样重要。随着我们将 AI 应用于日益复杂的科学模拟，像自步学习这样的“认知”策略很可能会成为鲁棒物理求解器的标准要求。