在深度学习的世界里，我们要么视参数为实现目的的手段。我们训练它们，保存它们，然后运行推理。但并非所有参数都是生而平等的。神经网络中的某些权重是至关重要的“承重柱”；而另一些则像是装饰性的修边，即使移除或修改也不会导致结构坍塌。

确定哪些参数最重要属于参数敏感性 (parameter sensitivity) 的范畴，而衡量这一指标的“黄金标准”工具是Fisher 信息矩阵 (Fisher Information Matrix, FIM) 。 Fisher 对角线告诉我们，如果扰动特定参数，模型的输出分布会发生多大变化。这对于模型融合 (Model Merging) 、网络剪枝 (Network Pruning) 和持续学习 (Continual Learning) 等先进技术至关重要。

这里存在一个问题: 计算 Fisher 的代价非常昂贵。它通常需要对训练数据进行单独的一轮遍历，计算每个样本的梯度，对它们进行平方，然后求和。对于大型语言模型 (LLM) ，这种开销可能是令人望而却步的。

但是，如果你不需要计算它呢？如果 Fisher 的一个近似值已经存在于你的 GPU 显存中，只是隐藏在显眼之处呢？

在论文 “Fishers for Free? Approximating the Fisher Information Matrix by Recycling the Squared Gradient Accumulator” 中，研究人员 YuXin Li、Felix Dangel、Derek Tam 和 Colin Raffel 提出了一种称为 “Squisher” 的方法。他们证明，自适应优化器 (如 Adam) 维护的平方梯度累加器可以被回收利用，以零额外成本近似 Fisher 对角线。

重要性的代价

要理解为什么 Squisher 是如此有用的发现，我们首先需要了解“昂贵”的做法。

Fisher 信息矩阵 (FIM)

Fisher 信息矩阵捕捉了损失概貌 (loss landscape) 的曲率。简单来说，如果损失概貌在某个参数周围非常陡峭，那么该参数就“很重要” (微小的变化会导致巨大的误差) 。如果概貌是平坦的，则该参数不太重要。

形式上，对于具有参数 \(\theta\)、输入 \(x\) 和标签 \(y\) 的神经网络，我们考察对数似然的梯度。标准 FIM 定义为梯度的期望协方差:

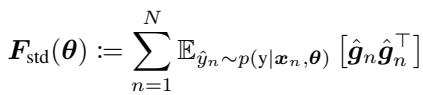
这里，\(\hat{g}_n\) 表示使用从模型自身分布中采样的标签计算出的梯度。

经验 Fisher (The Empirical Fisher)

在实践中，从模型分布中采样是很繁琐的。研究人员经常使用经验 Fisher , 它使用的是数据集提供的真实标签，而不是模型的预测分布:

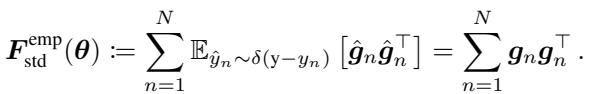
由于对于深度网络来说存储完整的矩阵 (大小为 \(P \times P\)，其中 \(P\) 是参数数量) 是不可能的，我们几乎只使用对角 Fisher 。 这将计算简化为每个样本梯度的平方和:

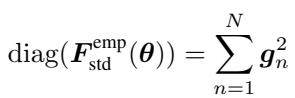
瓶颈

仔细看上面的公式。要计算它，你需要访问训练数据。你需要对 \(N\) 个样本执行前向和后向传播。至关重要的是，你需要在求和之前对每个样本的梯度进行平方。大多数深度学习框架都是针对*批次 (batch) *进行优化的，即在你看到梯度之前就已经对其取了平均。获取每个样本的平方梯度通常需要低效的循环或像 BackPACK 这样的专用库。

这种计算上的摩擦阻碍了许多从业者使用强大的基于 Fisher 的技术。

Squisher 登场

这篇论文的作者做出了一个敏锐的观察: 现代训练不仅仅使用原始的随机梯度下降 (SGD) 。我们使用的是像 Adam、AdamW 或 RMSProp 这样的自适应优化器。

这些优化器的工作原理是为每个参数单独调整学习率。为了做到这一点，它们会跟踪梯度的“二阶矩”——本质上是平方梯度的移动平均值。

在 Adam 中，这个累加器表示为 \(v^{(t)}\)，在每一步 \(t\) 进行更新:

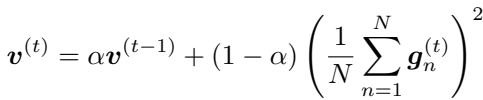
这里，\(g_n\) 是当前批次中的梯度。括号中的项是批次的平均梯度。

直觉上的跨越

作者问了一个简单的问题: Adam 的 \(v^{(t)}\) 是 Fisher 对角线的近似值吗?

乍一看，它们看起来很相似。两者都涉及平方梯度。

1. Fisher: 平方梯度的总和 (\(\sum g^2\))。
2. Adam: 批次梯度平方的移动平均 (\(\text{Avg}(\dots (\sum g)^2 \dots)\))。

然而，这里存在明显的数学差异。Fisher 是对平方求和；Adam 是对 (批次的) 和求平方。在统计学中，和的平方通常不等于平方的和。

为了弥合这一差距，作者利用了联合经验 Fisher (Joint Empirical Fisher) 的概念。如果我们不将每个数据点视为独立的随机变量，而是将整个数据集 (或批次) 视为一个联合分布，数学公式就会发生变化。联合经验 Fisher 实际上是由聚合梯度的外积定义的:

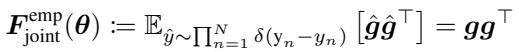
而它的对角线仅仅是求和后的梯度的平方:

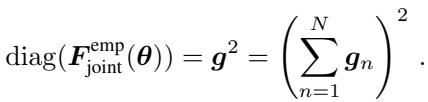
这揭示了理论上的联系。Adam 中的平方梯度累加器 (\(v^{(t)}\)) 本质上是在跟踪联合经验 Fisher 的移动平均值 (按批次大小缩放) 。

Squisher 的配方

所提出的方法被称为 “Squisher” (Squared gradient accumulator as Fisher，即作为 Fisher 的平方梯度累加器) ，非常简单。你不需要运行复杂的训练后流程来计算 Fisher，只需获取 Adam 已经为你计算好的优化器状态。

你可以通过回收利用 \(v^{(t)}\) 来近似 Fisher 对角线:

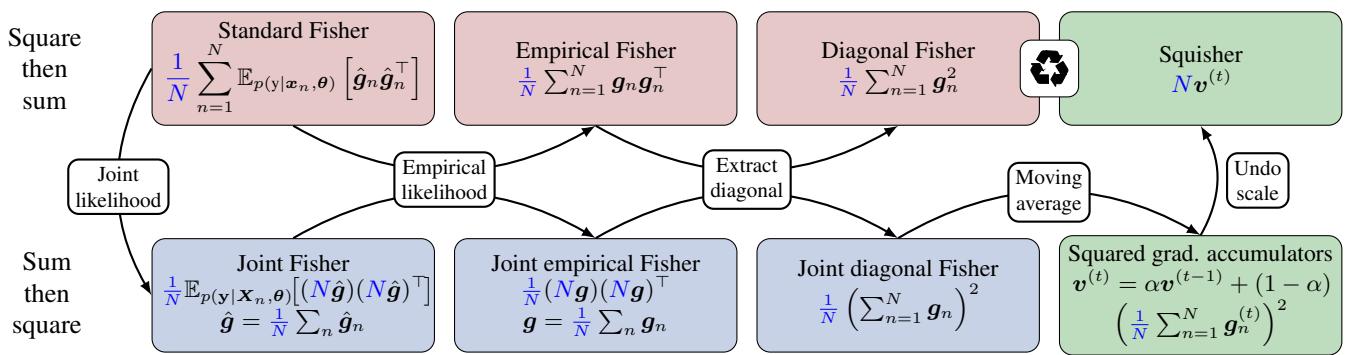
如图 1 所示，Squisher 充当了一条捷径。我们不再走“先平方再求和” (标准 Fisher) 的计算路径，而是接受 Adam 中固有的“先求和再平方”路径。

在比例上需要做一个小的调整。标准 Fisher 随数据点数量 \(N\) 缩放。因此，为了匹配标准 Fisher 的量级，我们可以缩放优化器状态:

在许多应用中 (如对参数进行排序以进行剪枝) ，绝对比例并不重要，重要的是相对顺序。在这些情况下，你可以直接使用 \(v^{(t)}\)。

它真的有效吗？

理论上很方便，但在实践中，用一个“粗糙”的移动平均值 (Squisher) 来代替严格的统计指标 (Fisher) 真的有效吗？作者在通常使用 Fisher 对角线的五个不同应用中对此进行了测试。

结果惊人地一致: Squisher 的表现与 Fisher 相当，且两者都显著优于基线。

让我们看看具体的实验。

1. 模型融合 (Model Merging)

模型融合涉及在不重新训练的情况下将两个不同的微调模型组合成一个。一种流行的技术, Fisher 融合 , 采用参数的加权平均值。如果模型 A 对特定参数具有较高的 Fisher 值 (意味着它很重要) ，而模型 B 的值较低，则融合后的模型将保持更接近模型 A 的值。

研究人员在针对各种文本数据集微调的 T5 模型上测试了这一点。

如图 2 的第一个面板所示，Squisher (橙色) 在这种设置下的表现实际上略好于标准 Fisher (蓝色) 。两者都远优于简单的平均 (Linear) 。由于融合依赖于相对重要性，这种近似方法完全站得住脚。

2. 基于不确定性的梯度匹配 (UBGM)

UBGM 是一种更高级的融合技术，试图对齐多个模型的梯度更新。它严重依赖 Fisher 矩阵来确定更新的方向。

UBGM 的更新规则很复杂，依赖于 Fisher 之和的逆矩阵:

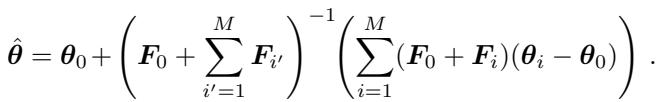
尽管如此复杂，用 Squisher 累加器替换 Fisher 矩阵 \(F_i\) 产生了几乎相同的准确率 (RoBERTa 模型上为 94.00% vs 93.99%) 。

3. 网络剪枝 (Network Pruning)

剪枝旨在移除参数以使网络更小、更快。逻辑很简单: 移除对损失影响最小的参数。Fisher 对角线为这种“显著性 (saliency) ”提供了一个度量标准。

使用 Fisher 的剪枝标准是:

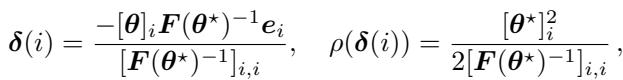
作者在 CIFAR-100 上对 VGG-13 网络进行了剪枝。即使移除了 75% 的参数，基于 Squisher 的剪枝仍然与昂贵的 Fisher 计算具有竞争力，并且远好于随机剪枝。

4. FISH 掩码 (FISH Mask)

与剪枝类似，“稀疏训练”涉及仅训练参数的一个子集。 FISH 掩码技术根据 Fisher 对角线选择要训练的参数。

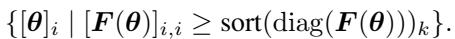
在 GLUE 基准上微调 BERT 的实验中，Squisher 几乎完全匹配 Fisher (准确率在 0.1% 以内) 。这证实了 Squisher 对参数重要性的排序与真实的 Fisher 几乎完全相同。

5. 任务嵌入 (Task Embeddings / Task2Vec)

我们可以使用在该任务上训练的模型的 Fisher 信息将整个“任务”嵌入到向量空间中。这有助于预测哪些任务是相似的 (例如，“问答”是否类似于“阅读理解”？) 。

任务之间的距离使用其 Fisher 矩阵的余弦相似度来衡量:

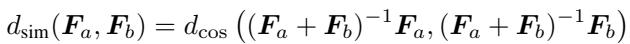
使用 Squisher 进行这些嵌入实际上在预测任务可迁移性方面产生了比标准 Fisher 更好的结果。这表明 Adam 的移动平均特性可能比静态的训练后计算捕捉到了更多关于训练轨迹的鲁棒信息。

6. 持续学习 (EWC)

最后，弹性权重巩固 (Elastic Weight Consolidation, EWC) 防止模型在学习新任务时“遗忘”旧任务。它通过惩罚对前一个任务很重要的参数的变化来实现这一点。

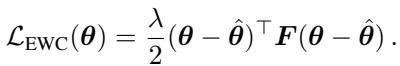
在这个方程中，\(F\) 充当惩罚权重。这是量级至关重要的一个设置。如果 Squisher 的值太小，正则化就会太弱；如果太大，模型就无法学习新任务。

作者发现，通过将缩放因子 \(N\) (数据集大小) 应用于 Squisher，他们在 Split-MNIST 和 CIFAR-100 基准测试中实现了与标准 EWC 相当的性能。

“免费”的优势

性能结果令人信服，但 Squisher 真正的卖点是效率。

计算 Fisher 是一个独立的、训练后的阶段。它需要加载模型、加载数据集并执行繁重的计算。然而，Squisher 是训练的副产品。如果你保存了优化器状态 (例如，PyTorch 中的 optimizer.state_dict()) ，你就拥有了 Squisher。

时间上的差异是巨大的:

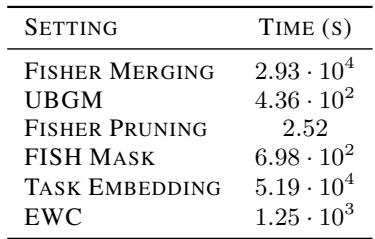
如表 1 所示，为模型融合计算 Fisher 花费了近 30,000 秒 (超过 8 小时) 。 Squisher 实际上花费了 0 秒 。 对于计算资源有限的研究人员，或者需要快速迭代的应用来说，这是一个颠覆性的改变。

细微差别与局限性

它是一个完美的替代品吗？并不总是。作者进行了消融研究 (表 2) 以了解其局限性。

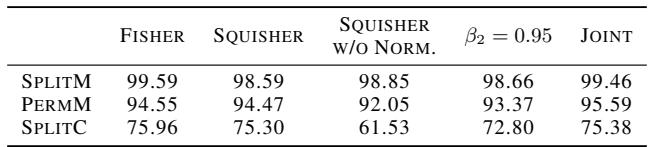
1. 缩放对 EWC 至关重要: 正如“Squisher w/o Norm”一栏所示，在正则化强度取决于 Fisher 绝对值的持续学习设置中，如果不对累加器进行 \(N\) 倍缩放，性能会严重下降。
2. 移动平均: Fisher 是整个数据集的总和。Adam 是指数移动平均 (EMA) 。如果 EMA 衰减率 (\(\beta_2\)) 太高或太低，近似值可能会发生漂移。然而，标准的 Adam 设置 (\(\beta_2=0.999\)) 效果良好。
3. 训练时长: 为了使 Squisher 准确，模型需要充分收敛，以便移动平均值稳定下来。在训练的早期阶段，Squisher 可能会有噪声。

结论

“Squisher”代表了效率的胜利。它提醒我们，我们努力计算的复杂统计数据——如 Fisher 信息矩阵——往往反映在我们已经使用的启发式工具中，比如 Adam。

通过认识到平方梯度累加器与联合经验 Fisher 之间的数学联系，作者解锁了一种几乎免费执行高级模型融合、剪枝和分析的方法。

给学生的关键要点:

• 不要删除你的优化器状态: 它们包含了关于损失地形几何形状的宝贵信息。
• 近似是强大的: Fisher 的理论定义是严格的，但在深度学习中，像 Squisher 这样“足够好”的代理通常会产生相同的下游结果。
• Fisher 是多才多艺的: 从融合 LLM 到防止灾难性遗忘，知道哪些参数重要是 ML 工具箱中最有用的工具之一。现在，它也是最容易获取的工具之一。

所以，下次当你完成模型训练时，不要只保存权重。保留 Squisher——你可能会免费获得你的 Fisher 信息。