引言

在探索智能 (无论是人工智能还是生物智能) 的过程中，我们通常依赖一个基本假设: 如果两个系统以相同的方式执行相同的任务，那么它们处理信息的方式也一定相似。如果一个深度神经网络 (DNN) 以与人类相同的准确率和错误模式对图像进行分类，我们会倾向于认为该网络的内部“神经编码”与人类大脑是一致的。

但如果这个假设从根本上就是错的呢？

Braun、Grant 和 Saxe 发表的一篇题为 “Not all solutions are created equal” (并非所有解生而平等) 的迷人研究论文挑战了这一基石。研究人员深入研究了神经网络的数学原理，证明了一个令人震惊的事实: 功能和表征是可分离的 (dissociable) 。

你可以拥有两个行为完全相同 (输入相同，输出相同) 的网络，但它们使用的是完全不同的内部表征。反之，你也可能拥有内部结构相似但执行功能不同的网络。神经网络的这种“罗生门效应”表明，窥探“黑盒”内部比我们要想象的棘手得多。

在这篇文章中，我们将剖析这篇论文。我们将探索“解流形 (solution manifold) ”——即解决任务的权重组合的无限景观——并发现为什么有些解是“任务特定 (task-specific) ”的 (反映数据结构) ，而另一些则是“任务无关 (task-agnostic) ”的 (可能在权重中隐藏了一只看不见的大象) 。

可识别性问题

要理解这篇论文的贡献，我们首先需要理解可识别性 (identifiability) 的概念。在统计学和工程学中，如果一个系统的内部参数可以通过其行为被唯一确定，那么该系统就是可识别的。

现代神经网络在很大程度上是不可识别的 。 因为它们是过参数化的 (拥有的神经元远多于解决任务所严格需要的) ，所以存在许多不同的权重和偏置组合可以产生完全相同的输入-输出映射。

这对神经科学和 AI 的可解释性构成了巨大的挑战。如果我们通过记录神经活动 (表征) 来推断大脑区域的功能，或者如果我们分析 Transformer 模型的隐藏层来理解它是如何“思考”的，不可识别性问题表明我们的发现可能是任意的。我们可能只是在分析解的一个特定版本，而不是解的本质。

完美的实验室: 深度线性网络

为了在数学上解决这个问题，作者转向了深度线性网络 (Deep Linear Networks, DLNs) 。 虽然现代 AI 使用非线性激活函数 (如 ReLU 或 Sigmoid) ，但 DLN 使用线性变换。

\[ \hat { \mathbf { y } } _ { n } = \mathbf { W } _ { 2 } \mathbf { W } _ { 1 } \mathbf { x } _ { n } , \]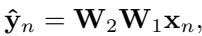

尽管很简单，DLN 与非线性网络具有重要的共同属性:

1. 它们具有非凸损失景观 (学习过程很复杂) 。
2. 它们具有形成内部表征的隐藏层。
3. 它们在分析上是易于处理的——我们可以通过精确的数学推导来求解，而不仅仅是猜测。

研究人员分析了一个训练用于最小化均方误差 (MSE) 的两层线性网络。

\[ \mathcal { L } _ { \mathrm { M S E } } = \frac { 1 } { 2 P } \sum _ { n = 1 } ^ { P } | | \hat { \mathbf { y } } _ { n } - \mathbf { y } _ { n } | | _ { 2 } ^ { 2 } \]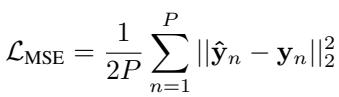

解流形

当我们训练网络时，我们是在寻找误差最小化的点。在过参数化网络中，这并不是一个单一的点 (全局最小值) ；它是一个由最优点组成的连通山谷，称为解流形 (Solution Manifold) 。

想象一个被群山环绕的平坦谷底。这片谷底上的每一点都能实现零误差 (或最小误差) 。你可以在这个谷底走动，改变你的坐标 (权重) ，而无需往上爬 (增加误差) 。

作者在图 1 中演示了这种“随机游走”。

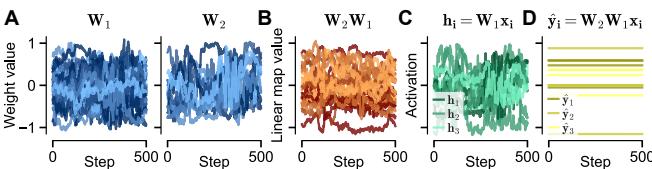
注意上图中的面板 (D) : 网络输出 (黄线) 从未改变。然而，看看 (A) 和 (B) : 权重矩阵正在发生显著漂移。最重要的是，看看 (C) : 隐藏层表征正在发生变化。

这证明了表征漂移 (representation drift) 可以在功能没有任何变化的情况下发生。一个神经系统可以有效地完全“重新连接”自己，同时保持其行为稳定。

绘制景观: 四种类型的解

如果存在无限的解，它们都是一样的吗？该论文将解流形分类为四个不同的区域，从最灵活到最受约束。这种分类是论文的理论核心。

解的结构取决于网络如何处理数据的不同子空间:

1. 相关输入 (Relevant Inputs) : 解决任务实际需要的信息。
2. 无关输入 (Irrelevant Inputs) : 输入中无法预测输出的特征 (噪声或干扰项) 。
3. 零空间 (Null Space) : 在训练数据中从未出现的输入方向。

让我们详细分析图 2 中展示的四种类型:

1. 一般线性解 (General Linear Solution, GLS)

这是解的“狂野西部”。它只要求两个权重矩阵的乘积 (\(W_2 W_1\)) 能正确地将输入映射到输出。

• 约束: 几乎没有。
• 行为: 输入权重 (\(W_1\)) 可以将无关噪声投射到隐藏层中，只要输出权重 (\(W_2\)) 将其“抵消”即可。
• 表征: 高度任意。隐藏层可以看起来像任何东西。

2. 最小二乘解 (Least-Squares Solution, LSS)

这种解最小化了功能范数。

• 约束: 它不对“幽灵”输入 (不存在的输入) 做出反应。
• 行为: 它仍然处理存在于训练数据中的无关特征。
• 表征: 仍然高度灵活且任务无关 (Task-Agnostic) 。

3. 最小表征范数解 (Minimum Representation-Norm Solution, MRNS)

这种解最小化了隐藏层活动的能量 (范数) 。

• 约束: 严格。它在第一层立即过滤掉所有无关信息。
• 行为: 隐藏层仅包含解决任务严格所需的信息。
• 表征: 唯一 (旋转意义下) 且任务特定 (Task-Specific) 。

4. 最小权重范数解 (Minimum Weight-Norm Solution, MWNS)

这最小化了权重本身的大小 (通常通过权重衰减正则化实现) 。

• 约束: 平衡。它在输入层和输出层之间平均分配“工作”。
• 表征: 唯一且任务特定 。

房间里的大象: 隐藏表征

这正是数学转化为惊人概念发现的地方。因为 GLS 和 LSS (灵活的解) 是任务无关的，它们的内部表征不必看起来像任务本身。事实上，它们可以是你想要的任何样子。

为了证明这一点，作者设计了一个“语义层级”任务 (分类植物、动物、物体等项目) 。然后，他们在数学上强制一个 GLS 网络完美地解决该任务，但加了一个特定的约束: 让隐藏层活动看起来像一头大象。

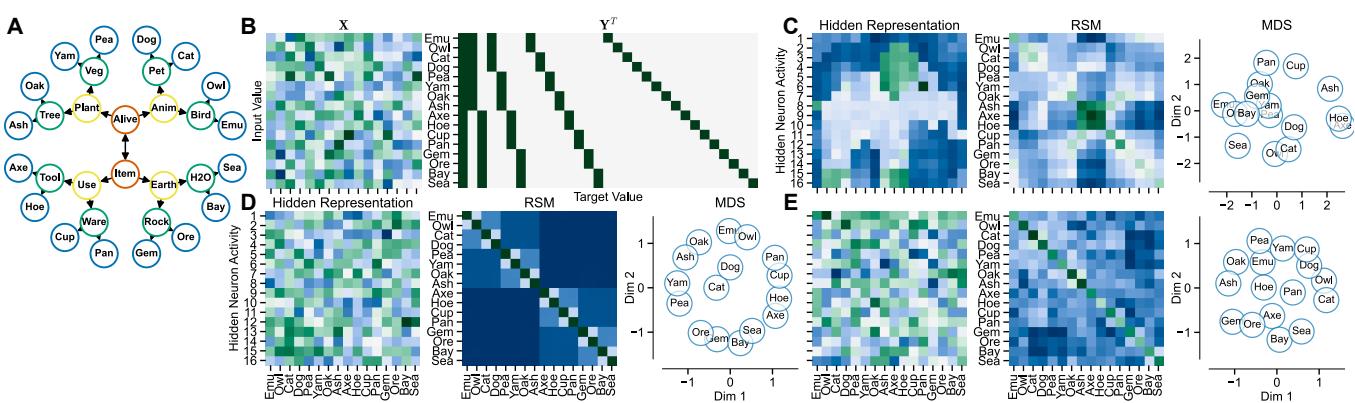
请看图 3 :

• C 行 (GLS): 隐藏表征 (左图) 实际上形成了一头大象的形状。中间的表征相似性矩阵 (RSM) 看起来像一个网格——它没有与任务相关的结构。然而，这个网络完美地解决了任务。
• D 行 (MRNS): 隐藏表征在肉眼看来是随机的，但 RSM 揭示了一个块状的层级结构。网络有效地在其大脑中将相似的概念 (动物与动物，植物与植物) 进行了“分组”。
• E 行 (MWNS): 与 MRNS 类似，显示出强烈的任务相关结构。

结论: 如果你分析一个网络 (或大脑) 并发现一个混乱或怪异的表征，这并不意味着系统没有工作。反之，你可以拥有两个解决相同问题的系统，其中一个按层级组织数据 (任务特定) ，而另一个将数据组织成大象的形状 (任务无关) 。

对神经科学和 AI 评估的启示

这种分离对于我们如何比较人工网络和生物大脑具有巨大的启示。两种常用的技术是线性可预测性 (Linear Predictivity) (我能不能根据一个网络的活动预测另一个网络的活动？) 和表征相似性分析 (RSA) (两个网络是否都认为“狗”和“猫”是相似的？) 。

作者进行了模拟，看看这些指标在不同类型的解中表现如何。

线性可预测性 (图 4A)

• 结果: 你可以很容易地从一个任务无关的表征预测出一个任务特定的表征 (因为无关表征拥有额外的自由度) 。
• 问题: 你通常无法从一个任务特定的表征预测出一个任务无关的表征。
• 结论: 低可预测性可能并不意味着功能上的差异；它可能只是意味着一个网络比另一个更“懒惰” (GLS) 并携带了更多无用信息。

RSA 相关性 (图 4B)

• 结果: 当比较任务无关的解 (GLS/LSS) 时，RSA 相关性剧烈波动 (波浪线) 。
• 结论: 如果你使用 RSA 来比较两个未被约束为高效 (任务特定) 的网络，你的结果本质上是随机的。你是在测量“大象”，而不是功能。

漂移的表征 (图 4C)

• 结果: 如果一个系统沿着解流形漂移 (随机游走) ，一个在时刻 0 训练的解码器将在时刻 100 失效，即使网络的行为并没有改变。
• 结论: 大脑中的“表征漂移”可能不是学习或遗忘；它可能只是在等效解流形上的随机游走。

驱动系统的因素是什么？噪声的作用

如果存在无限的解，为什么生物大脑 (以及许多人工网络) 似乎会收敛到结构化的、任务特定的表征上？为什么我们在视觉皮层中看不到“大象形状”的表征？

作者测试了三个假设:

1. 泛化 (Generalization) : 也许任务特定的表征能更好地泛化到新数据？

• 发现: 否。论文在分析上证明了泛化误差并不约束表征必须是任务特定的。

2. 输入噪声 (Input Noise) : 也许系统需要对嘈杂的感官数据具有鲁棒性？

• 发现: 否。对输入噪声的鲁棒性导致了 LSS (最小二乘解) 。正如我们所见，LSS 是任务无关的。它清理了输出，但允许混乱的内部表征。

3. 参数噪声 (Parameter Noise) : 也许系统需要对突触抖动 (噪声权重) 具有鲁棒性？

• 发现: 是。

作者推导了参数噪声下的预期损失:

\[ \begin{array} { r l r } { { \frac { 1 } { 2 P } \sum _ { n = 1 } ^ { P } | | ( \Omega _ { 2 } + \Xi _ { 2 } ) ( \Omega _ { 1 } + \Xi _ { 1 } ) ( \mathbf { x } _ { n } + \pmb { \xi } _ { \mathbf { x } _ { n } } ) - \mathbf { y } _ { n } | | _ { 2 } ^ { 2 } } } \\ & { } & \\ & { } & { = \frac { \sigma _ { \mathbf { x } } ^ { 2 } } { 2 } \big ( | | \Omega _ { 2 } \Omega _ { 1 } | | _ { F } ^ { 2 } + | | \Omega _ { 2 } | | _ { F } ^ { 2 } + | | \Omega _ { 1 } | | _ { F } ^ { 2 } \big ) \qquad ( 2 9 . } \\ & { } & \\ & { } & { \qquad + \frac { 1 } { 2 P } \big ( | | \Omega _ { 2 } | | _ { F } ^ { 2 } + | | \Omega _ { 1 } \mathbf { X } | | _ { F } ^ { 2 } \big ) + c , } \end{array} \]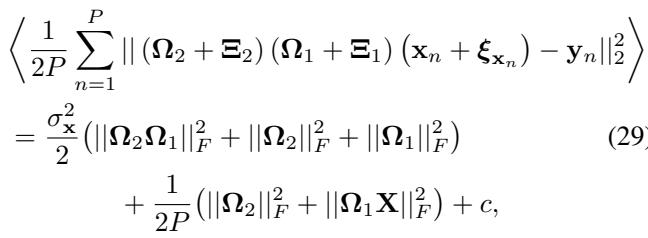

该方程表明，为了最小化参数噪声下的误差，网络必须最小化权重的范数 (\(\|\Omega\|_F^2\)) 和隐藏活动的范数 (\(\|\Omega_1 X\|_F^2\))。

结论: 对突触噪声具有鲁棒性的系统 (或经过重度正则化的人工网络) 会被迫进入 MRNS/MWNS 机制。它们必须丢弃无关信息。这种压力使表征与任务结构保持一致。

超越线性: 非线性网络

最后，有人可能会问: “这适用于使用 ReLU 和卷积的现代深度学习吗？”

作者表明，虽然非线性网络更难进行分析求解，但逻辑是成立的。他们在 MNIST (数字识别) 上训练了一个标准的 ReLU 网络，然后使用“保持功能的变换”在不改变预测的情况下扭曲隐藏层。

如图 5 所示，他们可以采用一个标准的 MNIST 网络 (面板 A) ，并在其隐藏表征中有效地“注入”一头大象 (面板 B) ，而不改变任何分类结果。

然而，就像线性情况一样，“扩展” (混乱) 的网络对参数噪声高度敏感 (面板 E，蓝/粉线) ，而最小化的、任务训练的网络 (黑线) 则具有鲁棒性。

总结与最终思考

这篇论文提供了一个严谨的数学警告，反对将网络做什么与网络如何思考混为一谈。

1. 分离: 网络的功能并不决定其内部表征。存在无限的变体。
2. 陷阱: 任务无关的解 (GLS) 可以在权重中隐藏任意信息 (如大象) ，从而使标准的比较工具 (RSA) 变得不可靠。
3. 约束: 对参数噪声的鲁棒性 (突触稳定性) 是迫使表征与任务结构一致的关键约束。

对于机器学习和神经科学的学生来说，这表明“表征学习”不仅仅是关于解决任务。它是关于在面对内部噪声时高效地解决任务。没有这个约束，机器中的幽灵可能看起来像任何东西。

---