引言

想象一下，试图预测一个复杂系统的运动，比如一组由弹簧连接的钟摆，或者在一个盒子中四处弹跳的带电粒子。在物理学和工程学中，这些被称为耦合动力系统 (Coupled Dynamical Systems) 。 为了对它们进行建模，我们不能仅仅孤立地观察一个物体；我们必须考虑到每个组件如何随时间与其他所有组件相互作用。

多年来，科学家们使用手工推导的微分方程来解决这些问题。但最近，深度学习已然入局。具体来说，一种被称为图常微分方程 (Graph Ordinary Differential Equations, GraphODE) 的框架显示出了巨大的潜力。通过结合图神经网络 (GNNs) 来模拟相互作用，并利用 ODE 求解器来模拟时间，这些网络理论上可以直接从数据中学习“物理定律”。

但这里有个陷阱。

大多数现有的 GraphODE 模型都在“作弊”。它们往往没有学习通用的物理定律 (如牛顿定律或库仑定律) ，而是记住了训练数据中的特定上下文。如果你在一个具有特定材料属性或相互作用强度的系统上训练它们，当你在这个条件稍有不同的系统上测试它们时，它们就会彻底失败。

在这篇文章中，我们将深入探讨一篇题为 “Rethink GraphODE Generalization within Coupled Dynamical System” (反思耦合动力系统中的 GraphODE 泛化) 的论文。研究人员提出了一个新的框架，称为 GREAT (具有解耦和正则化的可泛化 GraphODE) 。他们用因果视角审视这个问题，准确地指出了 为什么 当前的模型无法泛化，并提供了一个复杂的数学解决方案来修复它。

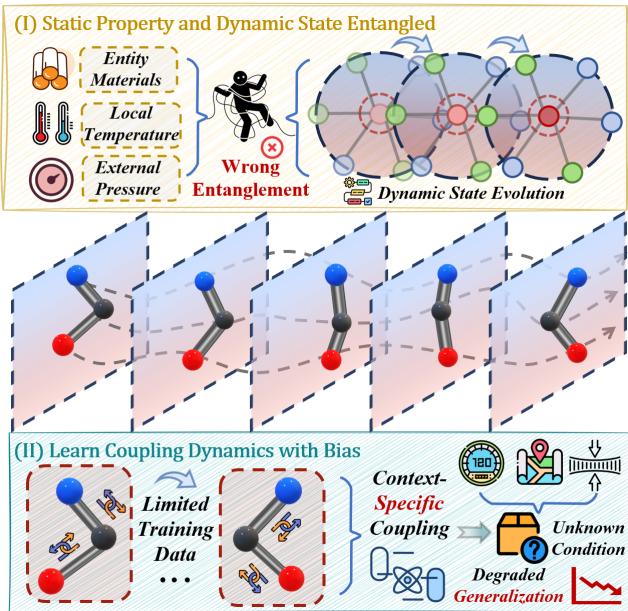
问题图示，展示了静态属性和上下文特定的耦合如何导致偏差。

如上方的 图 1 所示，核心问题有两个方面:

  1. 纠缠 (Entanglement) : 模型混淆了静态属性 (如质量或材料) 与动态状态 (如速度) 。
  2. 虚假耦合 (Spurious Coupling) : 模型过拟合了训练集中的特定相互作用模式，而不是学习相互作用的底层规则。

让我们来看看 GREAT 是如何解决这个问题的。

背景: GraphODE 框架

要理解这个解决方案，我们首先需要了解基准模型。耦合动力系统本质上是一个随时间变化的图。节点代表实体 (如粒子) ，边代表相互作用 (如力) 。

在标准的神经 ODE (Neural ODE) 中，节点状态 \(h_i(t)\) 的演变由一个函数 \(g_\theta\) (一个神经网络) 控制。该网络观察节点的当前状态及其邻居的状态:

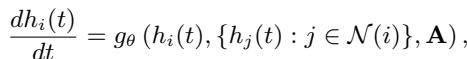
h_i(t) 导数的方程。

这里，\(\mathcal{N}(i)\) 代表节点 \(i\) 的邻居，\(\mathbf{A}\) 是定义图结构的邻接矩阵。为了求出系统在未来任意时间 \(t\) 的状态，我们需要从初始状态 \(h_i(t_0)\) 开始对这个微分方程进行积分:

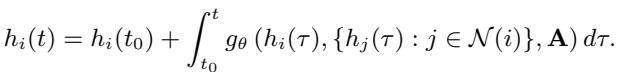
神经 ODE 的积分形式。

初始状态本身通常由一个编码器网络学习，该网络观察一小段历史观测数据:

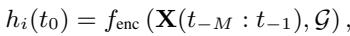
编码器函数方程。

最后，通过最小化预测轨迹与实际地面真值 (ground truth) 轨迹之间的差异来训练模型:

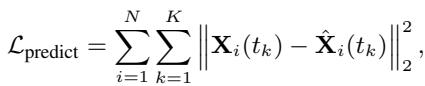
测量预测误差的损失函数。

虽然这种设置对于“分布内 (in-distribution) ”数据 (即看起来与训练集完全相同的数据) 效果很好，但当物理参数发生变化时，它就会崩溃。研究人员认为，这种崩溃的发生是因为模型缺乏对系统的因果理解。

一个因果视角

作者引入了结构因果模型 (Structural Causal Model, SCM) 来分析该系统。SCM 允许我们画出一个图表，展示变量之间如何相互影响，并识别出误导模型的“后门路径 (backdoor paths) ”—即虚假相关性。

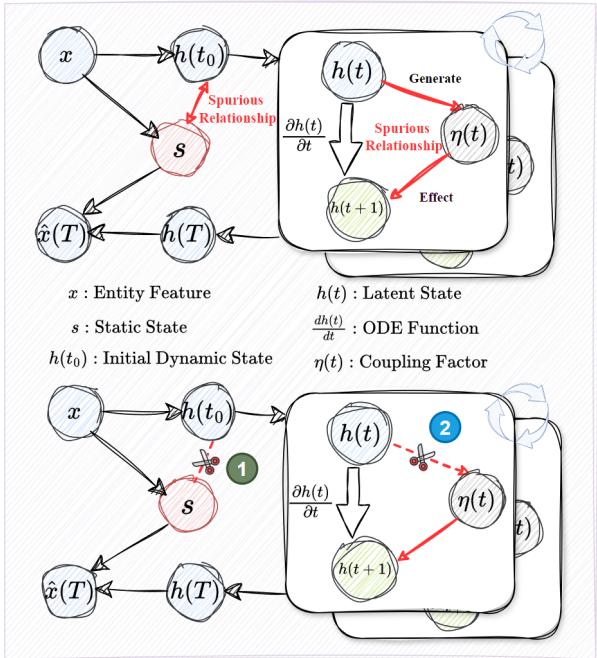
结构因果模型图，展示了实体特征、静态状态和动态状态之间的关系。

图 2 强调了标准 GraphODE 中的两个关键缺陷:

  1. 静态混淆因子 (The Static Confounder, \(x \to s \to h(t)\)) : 输入特征 \(x\) 包含静态信息 (例如质量) 和动态信息 (例如速度) 。静态信息 \(s\) 应该只影响 初始 设置。然而，标准编码器将 \(s\) 混入到了动态状态演变 \(h(t) \to h(t+1)\) 中。如果模型依赖静态“捷径”来预测运动，当这些静态属性改变时，模型就会失败。
  2. 耦合混淆因子 (The Coupling Confounder, \(h(t) \to \eta(t) \to h(t+1)\)) : 耦合因子 \(\eta(t)\) 代表相互作用的强度。在训练中，特定状态可能纯粹出于偶然或上下文原因与特定耦合强度相关联。模型学习到了这种偏差，而不是通用的相互作用定律。

为了构建一个 可泛化的 GraphODE (Generalizable GraphODE) , 作者提出了一个新的控制方程，其中显式包含了耦合因子 \(\eta_{i,j}(t)\):

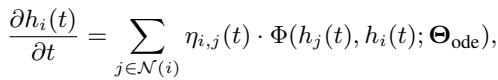
带有耦合因子的可泛化 GraphODE 方程。

在这里，目标是学习 \(\Theta_{ode}\) (物理定律) ，使其无论在什么具体上下文中都成立。

GREAT 方法

GREAT 框架 (Generalizable GraphODE with disentanglement and regularization) 使用两个独特的模块来解决这两个因果缺陷。

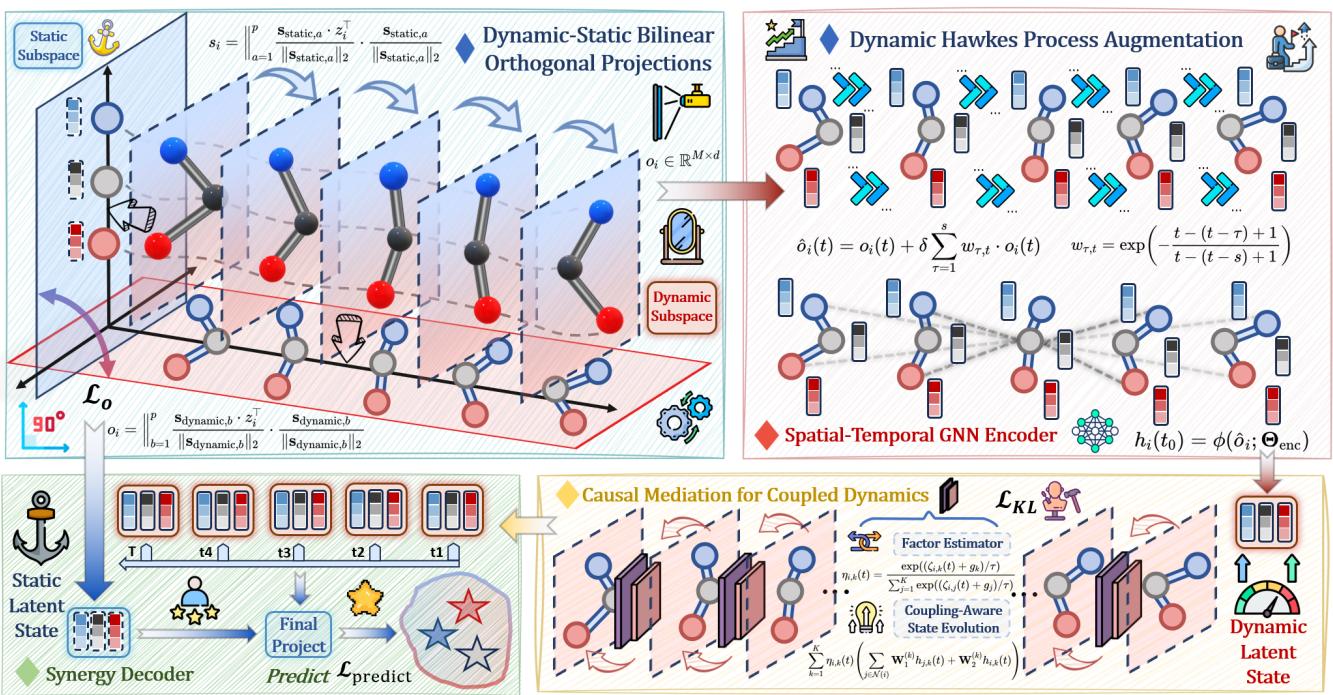
GREAT 框架的详细架构。

如架构图( 图 3 )所示，工作流程分为:

  1. DyStaED (左上) : 解耦静态和动态状态。
  2. CMCD (右下) : 因果中介以修复耦合偏差。

让我们逐一拆解。

1. 动态-静态平衡解耦器 (DyStaED)

第一步是确保“物体是什么”不会与“物体在做什么”混淆。编码器生成一个潜在状态 \(z_i\)。作者的目标是将其分解为两个正交的分量: 动态部分 \(o_i\) 和静态部分 \(s_i\)。

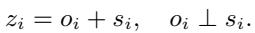
z 分解为 o 和 s。

正交子空间投影

为了在数学上实现这种分离，模型学习两个特定的子空间 (坐标系) : 一个用于静态特征，另一个用于动态特征。

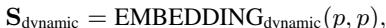
静态子空间嵌入方程。 动态子空间嵌入方程。

模型将潜在状态 \(z_i\) 投影到这些子空间上。这就像是在 3D 空间中取一个向量，并将其分离为 X 轴分量和 Y 轴分量。

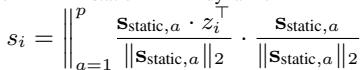
静态分量 \(s_i\) 通过将 \(z_i\) 投影到静态基向量上来计算: 静态分量的投影方程。

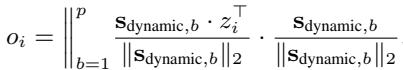
同样，动态分量 \(o_i\) 使用动态基向量求得: 动态分量的投影方程。

为了确保这两个分量真正不同且不共享信息，作者施加了一个 正交性损失 (Orthogonality Loss) 。 这强制静态和动态子空间相互垂直 (余弦相似度为 0) 。

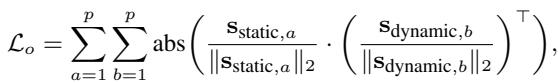
正交性损失函数。

动态霍克斯过程增强 (Dynamic Hawkes Process Augmentation)

仅仅分离状态是不够的。物理系统具有“惯性”或历史——过去的状态会影响现在。为了捕捉这种自激特性，作者使用 霍克斯过程 (Hawkes Process) 来增强动态状态。这种机制允许当前的动态状态受到其历史加权和的影响。

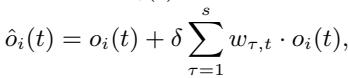
霍克斯过程增强方程。

权重随时间衰减，这意味着最近的历史比久远的历史更重要:

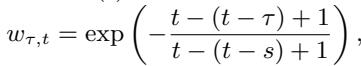
权重衰减方程。

这产生了一个鲁棒的初始状态 \(h_i(t_0)\)，它包含丰富的动态信息，但不含静态属性。

2. 耦合动力学的因果中介 (CMCD)

现在我们有了一个干净的动态状态，我们需要解决第二个问题: 有偏差的耦合。我们希望模型基于 通用规则 来学习物体如何相互作用，而不是基于训练数据的特定上下文。

用因果术语来说，我们要执行一次 干预 (intervention) 。 我们要问: “如果我们设定初始状态，移除虚假耦合相关性的影响，系统会发生什么？”

在数学上，研究人员希望估计给定初始状态干预 \(do(h_i(t_0))\) 下的轨迹概率。这很难，因为“真实的”耦合因子 \(\eta\) 是不可观测的 (潜在的) 。

变分推断

作者使用变分推断来解决这个问题。他们将耦合因子 \(\eta_i(t)\) 视为一个潜变量。他们推导出一个训练目标 (证据下界或 ELBO) ，试图在正则化耦合因子的同时重建轨迹。

核心思想是用一个更简单的分布 \(q\) 来近似真实的耦合分布。推导出的损失函数包含一个 KL 散度 (KL Divergence) 项:

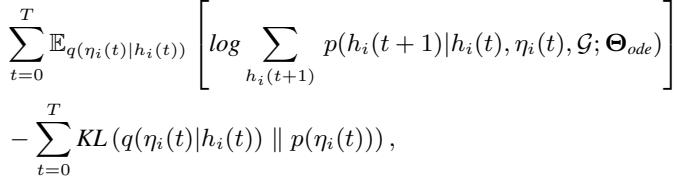
展示带有 KL 散度的 ELBO 推导方程。

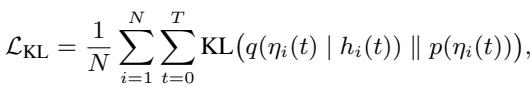
KL 散度损失项。

这个 KL 项强制学习到的耦合分布 \(q(\eta_i(t) | h_i(t))\) 接近一个“上下文无关”的先验分布 \(p(\eta_i(t))\)。本质上，它防止模型将耦合逻辑过拟合到特定的训练场景中。

因子估计器与演化

但是我们如何实际获得耦合因子 \(\eta\) 的值呢？模型使用 Gumbel-Softmax 方法从动态状态中估计它。这允许模型采样离散的耦合“模式”，同时保持可微性 (这样我们就可以用反向传播来训练它) 。

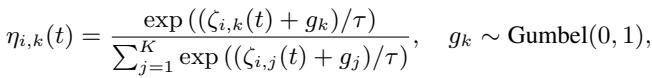
耦合因子的 Gumbel-Softmax 方程。

最后，为了允许复杂的周期性行为 (如弹簧振荡) ，动态状态被分解为三角函数子状态 (正弦和余弦分量) 。

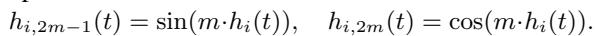
三角函数基分解。

求解器积分的最终微分方程如下所示:

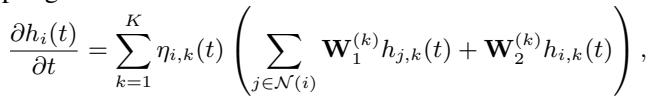
最终状态演化方程。

在这里，状态演化是相互作用的加权和，并由学习到的因果耦合因子 \(\eta_{i,k}(t)\) 进行调节。

总损失函数

模型使用组合损失函数进行端到端训练:

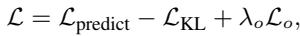
总损失函数方程。

这结合了:

  1. 预测准确性 (\(\mathcal{L}_{predict}\)): 轨迹是否与现实相符？
  2. 因果正则化 (\(\mathcal{L}_{KL}\)): 耦合逻辑是否无偏？
  3. 解耦 (\(\mathcal{L}_{o}\)): 静态和动态状态是否已分离？

实验与结果

作者在三个基于物理的数据集上测试了 GREAT:

  1. SPRING: 由弹簧连接的质量块 (胡克定律) 。
  2. CHARGED: 通过库仑力相互作用的带电粒子。
  3. PENDULUM: 连接的钟摆链。

他们评估了两种设置:

  • 分布内 (ID): 测试数据与训练数据具有相同的参数范围。
  • 分布外 (OOD): 测试数据具有不同的参数 (例如，更重的质量、更强的电荷、不同的初始速度) ，以测试泛化能力。

性能比较

下方的 表 1 展示了结果 (RMSE 是均方根误差，越低越好) 。

比较 GREAT 与其他方法的表格。

关键结论:

  • 主导地位: GREAT 在几乎所有类别中都取得了最佳性能 (粗体) 。
  • OOD 泛化: 在分布外 (Out-of-Distribution) 列中，GREAT 与其他模型 (如 LG-ODE 或 TREAT) 之间的差距巨大。这证明了因果解耦使模型比标准方法能更好地适应新的物理环境。

轨迹可视化

数字虽好，但眼见为实。 图 4 可视化了 SPRING 数据集 (OOD 设置) 中粒子的预测路径。

轨迹可视化比较。

  • 地面真值 (左): 实际路径。
  • GREAT (左数第二): 几乎与地面真值完美重叠。
  • 竞争对手 (右): 注意 TREAT 和 LG-ODE 如何显着偏离真实路径。它们在训练期间“学到了”错误的物理知识，无法适应 OOD 参数。

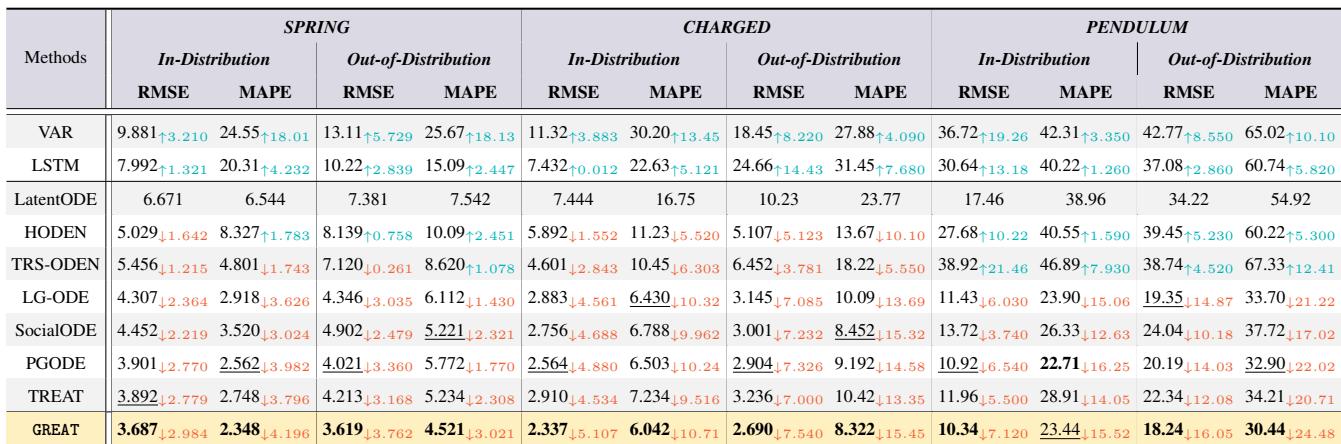
组件重要吗？ (消融研究)

作者还检查了是否解耦器 (DyStaED) 和因果中介 (CMCD) 都是必要的。

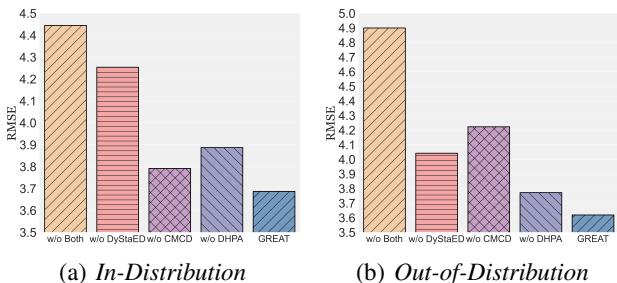
消融研究柱状图。

图 5 显示，移除任一组件都会增加误差 (RMSE) 。

  • w/o DyStaED: 移除静态/动态分离会损害性能。
  • w/o CMCD: 移除因果耦合正则化造成的损害更大，尤其是在 OOD 设置中。
  • w/o Both: 误差飙升。

长期预测

最后，他们测试了模型对未来较长时间的预测能力。

预测长度分析图。

图 6 显示，随着预测范围 (X 轴) 的增加，所有模型的误差都会上升 (这在混沌理论中是预期的) 。然而，与其他模型相比，GREAT (红线) 保持了低得多的误差率，表现出卓越的稳定性。

结论

GREAT 论文代表了将深度学习与科学建模相结合的重要一步。通过将学习过程视为因果推断问题，而不仅仅是曲线拟合，作者成功构建了一个不仅能记忆数据，还能开始理解底层机制的模型。

两个关键创新——用于将“物体是什么”与“物体如何运动”分离开的 DyStaED , 以及用于学习无偏相互作用规则的 CMCD——使得该模型能够以传统 GraphODE 无法做到的方式泛化到新环境。

对于“AI for Science (科学智能) ”领域的学生和研究人员来说，这强调了一个至关重要的教训: 在对物理世界进行建模时，仅靠架构是不够的。我们必须仔细考虑变量的因果结构，以确保我们的模型学习的是自然法则，而不仅仅是我们数据集中的偏差。