像 GPT-4 这样的大语言模型 (LLM) 重新定义了人工智能的边界。它们能够生成代码、撰写文章,并以近乎人类的流畅度解释概念。然而,尽管它们功能强大,其内部工作机制仍然在很大程度上是个谜。这些模型内部包含数十亿个参数,构成了错综复杂的连接网络——复杂到我们常常将其称作“黑箱”。我们可以观察输入和输出,但无法理解中间的推理过程。
缺乏透明性不仅是一个学术问题;它更是一个关乎安全、信任与对齐的现实挑战。如果无法理解模型为何选择某一特定输出,就无法在关键情境中预测或验证其行为。
机制可解释性领域旨在破解这一谜题。它试图对神经网络进行逆向工程,追踪产生特定行为的内部“回路”。在 OpenAI 的论文 《权重稀疏的 Transformer 具有可解释的回路》 中,研究者为这一挑战提出了全新的思路: 他们没有去剖析一个密集模型,而是直接构建一个从设计层面上可解释的 Transformer——在训练过程中强制其大部分权重为零。
通过强制稀疏,最终得到的模型变得极其简洁,内部计算被分解为清晰且可被人类理解的算法。由此诞生的神经回路可以被精确地映射、描述和验证。
问题所在: 叠加 (Superposition)
在介绍方法之前,我们需要理解神经网络可解释性中的一个主要障碍: 叠加 (superposition) 。
想象你拥有一个很小的衣柜 (模型的神经元) 和庞大的衣物集合 (模型要表示的概念) 。为了把所有东西都塞进去,你不得不将多套衣服挤进同一个格子。某个神经元可能同时响应“红色”、“危险”和“句子结尾”。这种多个特征共享同一个神经元的纠缠现象,就是叠加。
在密集模型中,叠加现象极其普遍。这也是为什么“这个神经元检测引号开头”这样的解释常常只对了一部分——同一个神经元可能还代表完全无关的概念。这种多义性行为让模型的内部变得混乱难解。
机制可解释性的挑战在于解开这些重叠。要提高清晰度,就意味着要找到让模型独立表示单个概念的方法。
洞见: 用稀疏性强制实现简单性
作者提出了一种激进的简化方式: 允许模型具有巨大的容量,但禁止它使用其中的大部分。
他们训练了权重稀疏的 Transformer , 其中几乎所有连接——约每 1000 个中有 999 个——都被设置为零。这一约束促使神经元专门化。每个神经元只能连接到少数其他神经元,从而保证了紧凑且解耦的计算。结果是模型内部的回路更易于分离和解释。
该方法的工作流程包括两个主要阶段:
训练权重稀疏的 Transformer: 模型从零开始在 Python 代码数据集上进行预训练,并通过对权重施加 \( L_0 \) 范数惩罚来强制严格的稀疏性约束。
剪枝以发现可解释的回路: 训练完成后,研究人员识别出执行特定任务 (例如闭合字符串或预测列表末尾) 所需的最小节点子集——即回路。回路之外的节点会被消融,即将其激活值设置为训练分布中的恒定均值。
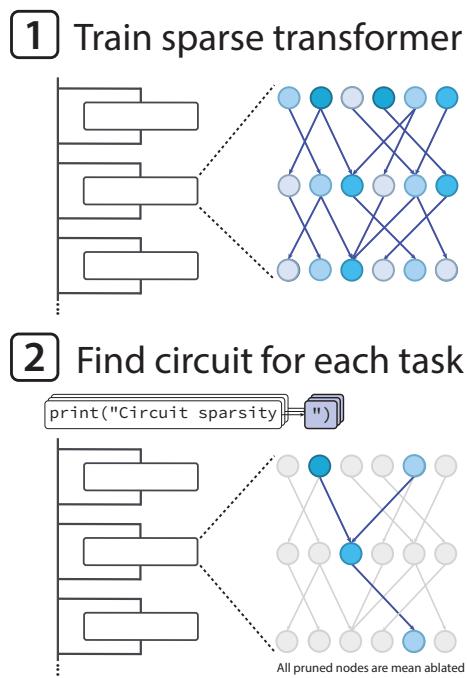
图 1. 研究工作流程: 先训练稀疏 Transformer,再对其剪枝,以分离出用于特定任务的可解释回路。
这一过程隔离出了既必要又充分的网络组件。回路越小,可解释性越高。
结果: 更简单的回路,更深刻的洞见
稀疏模型学习紧凑回路
为了量化评估可解释性,研究人员在 20 个小型 Python 编程任务上分别训练了稀疏与密集 Transformer——每个任务都要求离散推理能力 (例如决定使用 ] 还是 ]] 来闭合括号) 。他们对模型进行剪枝以达到同样的性能,并统计所得回路的规模。
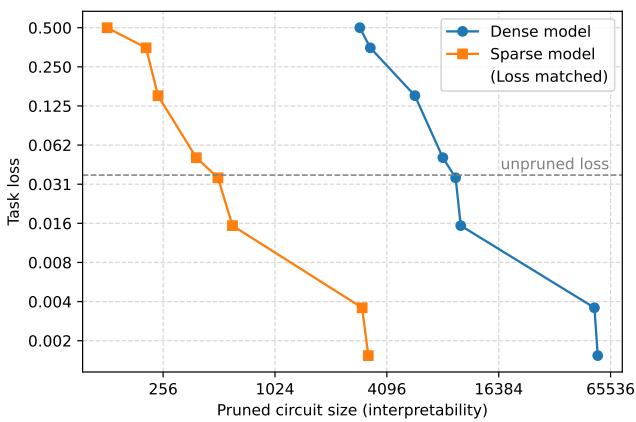
图 2. 稀疏模型产生的回路要小得多——在同等性能下约小 16 倍——展现出更清晰的内部组织。
稀疏模型以约16 倍更小的回路规模实现了与密集模型相似的准确率。这证明权重稀疏训练促使模型以解耦、局部的方式分配信息。
扩展可解释性与能力的边界
当然,强制稀疏会限制模型的总体能力。然而,图 3 展示了一条令人鼓舞的权衡曲线: 随着模型在保持非零参数数量不变的前提下变大,其能力与可解释性均提升。换句话说, 更大的稀疏模型可以同时更强大且更易理解 。
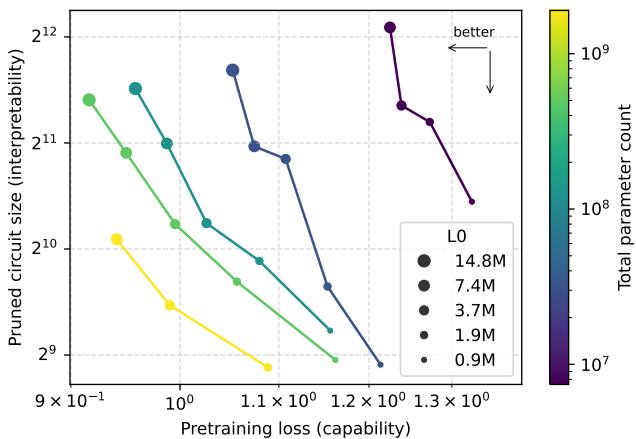
图 3. 在稀疏性约束下扩大总参数量可同时提升能力与可解释性——将帕累托前沿推向左下方。
这种扩展行为说明,可解释性在未来或许不必以牺牲性能为代价。
深入回路: 理解学到的算法
由于这些回路十分紧凑,研究者得以手动追踪其计算过程——以人类水平进行逆向工程。以下三个例子尤为突出。
回路 1: 模型如何闭合字符串
任务: 给定 Python 代码中的一个开引号 (' 或 ") ,预测匹配的闭合引号。
该回路仅包含 12 个节点和 9 条边,分为两个概念阶段:
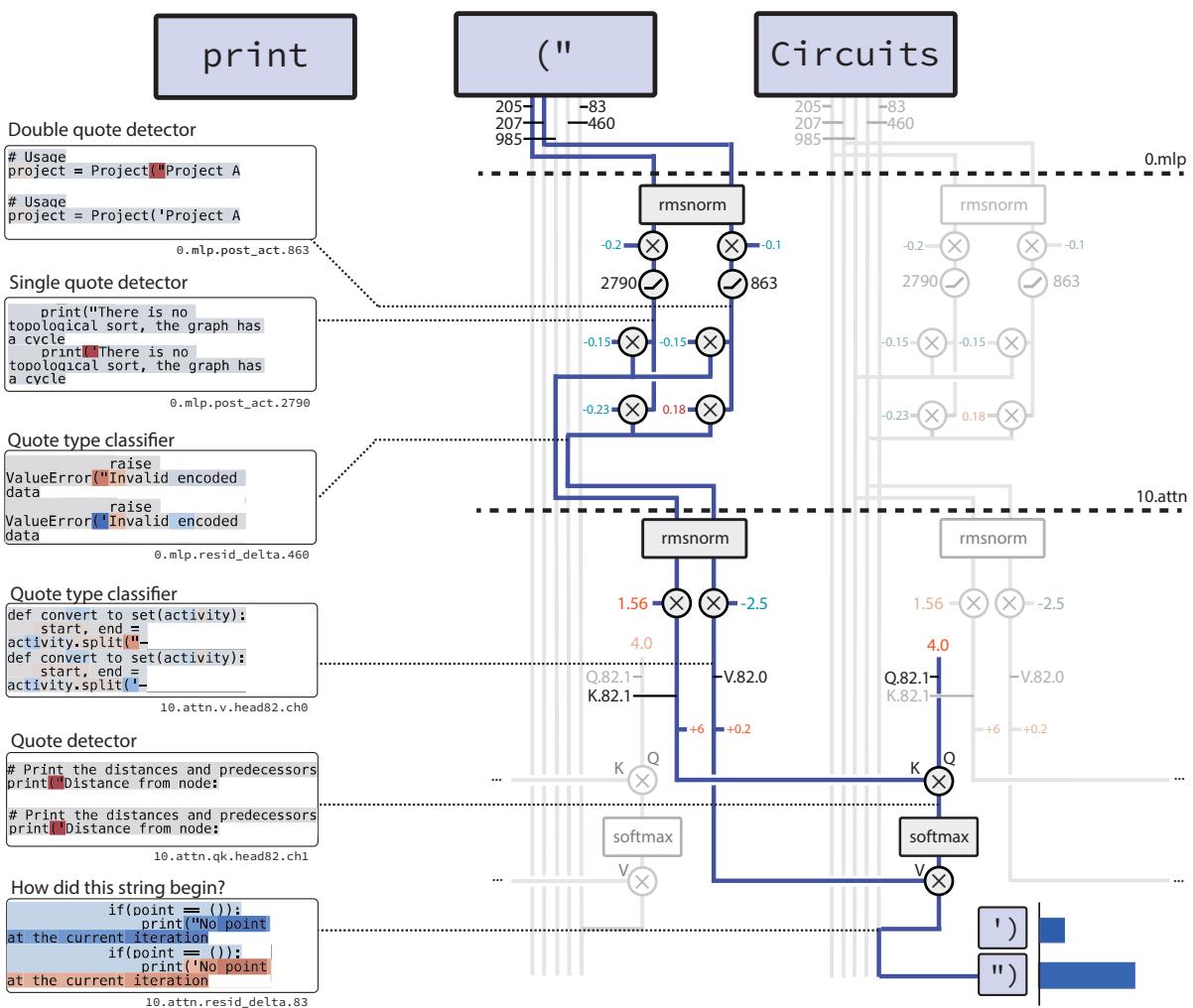
图 4. 闭合字符串回路: 两个神经元检测并分类引号,一个注意力头将正确引号类型向前复制。
- 检测: 第一个 MLP 层将词元嵌入转换为两个专门信号:
- 一个引号检测器神经元,响应任意引号标记;
- 一个引号类型分类器,对于双引号为正,对于单引号为负。
- 复制: 随后,一个注意力头利用这些信号生成正确的闭合引号。检测器作为键 (key) ,指示注意力头聚焦的词元;分类器作为值 (value) ,编码引号类型。输出直接对应正确的闭合符号。
这种精确而逐步的行为,与人类为闭合字符串字面量所写算法几乎完全一致。
回路 2: 计算嵌套列表
任务: 根据嵌套深度判断应使用 ] 还是 ]]。
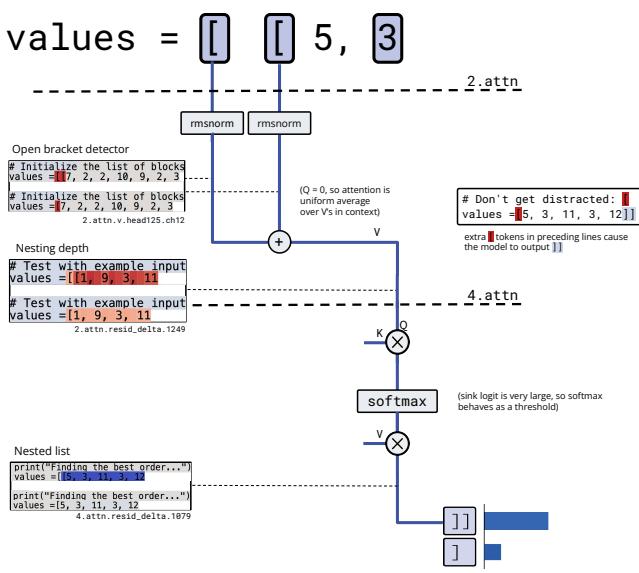
图 5. 括号计数回路: 检测开括号,对其表示进行平均以编码嵌套深度,并进行阈值处理以决定使用
]或]]。
该回路分为三个阶段运行:
检测: 当模型看到
[时,一个注意力值通道作为“开括号检测器”激活。通过平均计数: 下一个注意力头的查询与键几乎是恒定的,从而有效地对上下文中的“开括号检测信号”取平均值,并将平均激活写入残差流——即嵌套深度的表示。
阈值判定: 另一个头读取嵌套深度信号并应用 softmax 阈值: 深度嵌套激活高则输出
]],浅层激活低则输出]。
理解该算法后,研究者能够预测并制造对应的对抗性失败。长序列会稀释平均激活,降低嵌套深度,导致模型错误地输出单个闭括号。
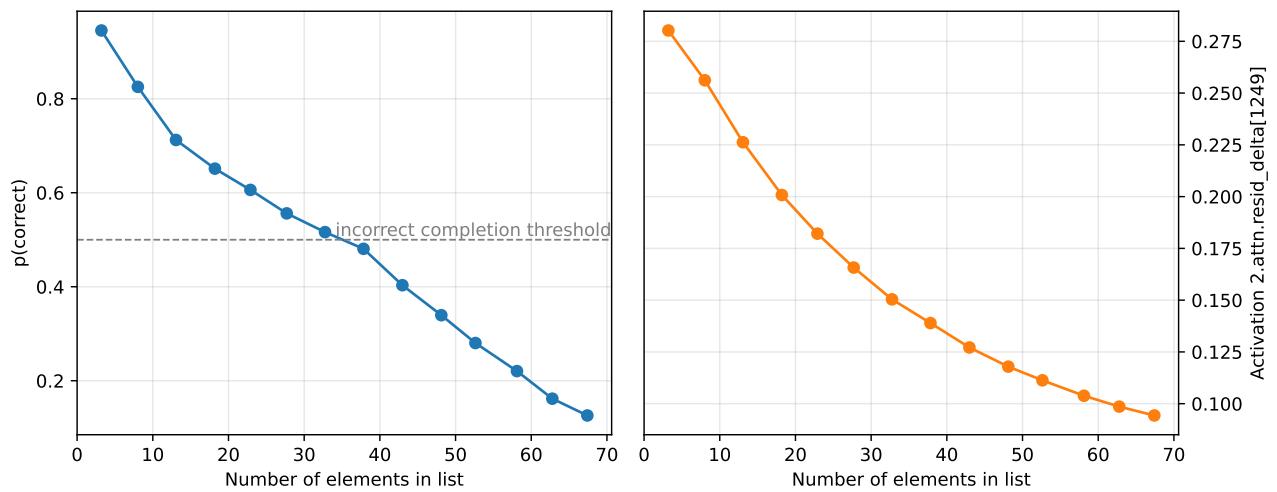
图 8. 随着列表变长,“上下文稀释”削弱了嵌套深度信号并降低准确率——证明了基于回路理解的预测能力。
回路 3: 追踪变量类型
任务: 判断一个变量是被初始化为 set() 还是字符串,以选择 .add 或 +=。

图 6. 变量类型追踪回路: 一个两跳算法跨词元复制类型信息并在稍后检索。
该回路使用两个注意力头,实现一个简单的信息查找算法:
- 第一跳: 第一个头将变量名 (
current) 复制到其初始化 (set()) 上下文,有效地用该名称“标记”类型。 - 第二跳: 当模型再次遇到
current时,第二个头从set()中检索标记信息并将其前向传递,从而实现正确的方法补全。
这样的复杂符号追踪行为竟能自然地从稀疏计算中涌现。
连接稀疏模型与密集模型
虽然稀疏模型更易于理解,但其训练成本高且效率较低。一个关键问题是: 这些洞见能否帮助我们理解现有的密集模型?
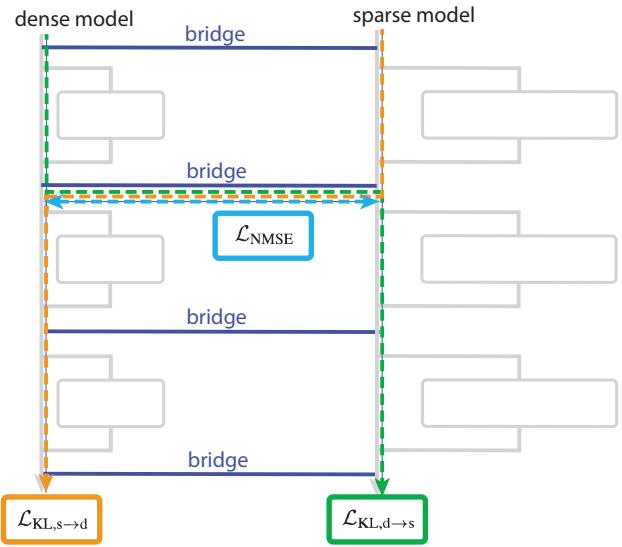
图 7. 桥接层连接密集模型与稀疏模型的对应层,校准内部激活,实现可解释性的迁移。
为此,研究人员引入了桥接 (bridges) ——在密集模型与稀疏模型对应层之间训练的线性映射。这些桥梁使两种模型的激活值可以互相转换,有效地实现了密集表示与可解释表示的配对。
通过这种机制,对稀疏模型中可解释通道的扰动可以投射到密集模型中,从而以可预测的方式引导其行为。
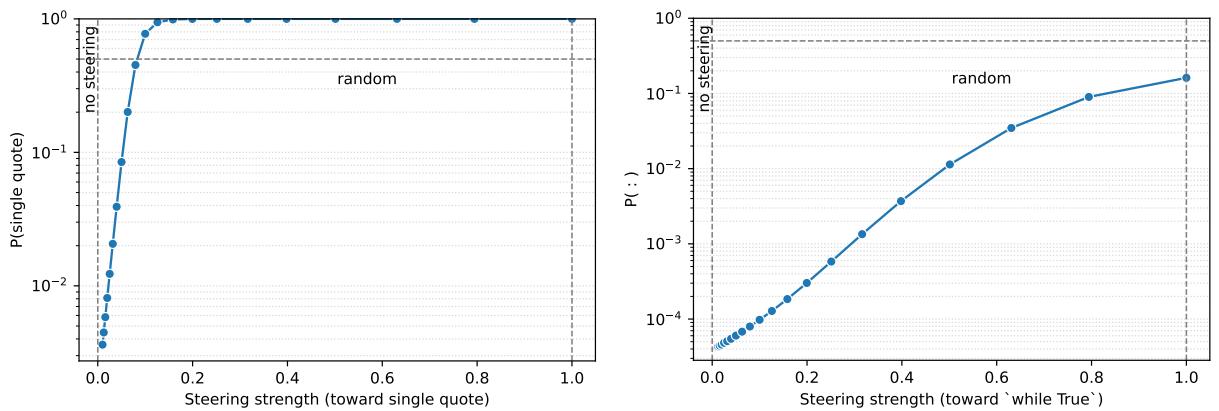
图 9. 通过稀疏-密集桥接的受控编辑展示了可解释激活如何引导密集模型的输出。
例如,在稀疏模型中操控“引号类型分类器”神经元并将其投射到密集模型后,会增加密集模型输出单引号的概率。这表明两种架构间存在潜在对齐——这是解读密集网络的第一步。
展望未来: 迈向透明智能
这项研究在让人工智能系统变得可理解的道路上迈出了重要一步。通过训练权重稀疏模型,研究者创造了推理过程可在单个连接层面被完整追踪的 Transformer。他们为语言任务展示了清晰、机械的算法——传统模型中几乎难以实现。
但该方法仍然计算昂贵。稀疏模型需要比密集模型更多的训练资源,因此暂不现实于大规模应用。未来的进展可能来自两个方向:
扩展“模型生物”: 构建规模逐步增大的稀疏模型——可解释的“模型生物”,规模至 GPT-3 级——有望揭示不同架构间共享的普遍回路模式。
聚焦关键任务: 使用桥接的稀疏模型研究小范围高风险领域——如前沿模型中的真实性与安全相关行为——可在不完全重新训练的前提下获得实用洞见。
最终,稀疏回路的意义不仅在于可解释性提升,更在于实现自动化的理解 。 通过构建内部语言清晰且结构化的模型,我们为未来人工智能能够自我推理奠定了基础。
通过这类研究,我们距离“AI 不再是黑箱,而是玻璃箱”的愿景又近了一步——一个强大而透明、高效且可解释、既有能力又负责任的智能世界。
