当你问一位教授一个简单的问题，比如“2 + 2 等于几？”，你期望得到一个简单的回答: “4”。但如果你问，“神经网络是如何学习的？”，你则期望得到一个详细的、分步骤的解释。

如果教授为了回答“2 + 2”而讲了二十分钟的数论课，你会感到困惑。反之，如果他们只用一个词来回答深度学习的问题，你将一无所获。

大语言模型 (LLM) 也面临着同样的问题。目前的提示 (Prompting) 技术，如思维链 (Chain-of-Thought, CoT) ，倾向于采用“一刀切”的方法。它们要么迫使模型在处理难题时过于简单，要么在处理简单问题时过于复杂。

在这篇文章中，我们将深入探讨一篇引人入胜的论文**“Adaptation-of-Thought: Learning Question Difficulty Improves Large Language Models for Reasoning” (思维适应: 学习问题难度以提升大语言模型的推理能力)** 。 研究人员提出了一种新方法 ADoT , 教导 LLM 评估问题的难度，并据此调整其推理过程。

推理中的“恰到好处”难题

为了让 LLM 在推理任务 (如数学应用题或常识逻辑) 中发挥最佳性能，研究人员使用提示工程 。 一种流行的方法是“少样本思维链 (Few-Shot Chain-of-Thought) ”，即在询问目标问题之前，给模型提供几个示例 (演示) ，包含问题及其分步解答。

然而，这里存在一个错配问题。

  • 简单的提示: 如果提示中的示例太简单，LLM 就不会触发解决复杂微积分或逻辑谜题所需的深度推理。
  • 复杂的提示: 如果示例非常详细且复杂 (就像 PHP 或 Complex-CoT 等方法中使用的那样) ，LLM 可能会过度思考简单的问题。它可能会产生不存在的步骤 (幻觉) ，或者迷失在自己的冗长描述中。

研究人员在 AQUA 数据集 (代数问题) 上分析了这一现象。请看下面的分类细目:

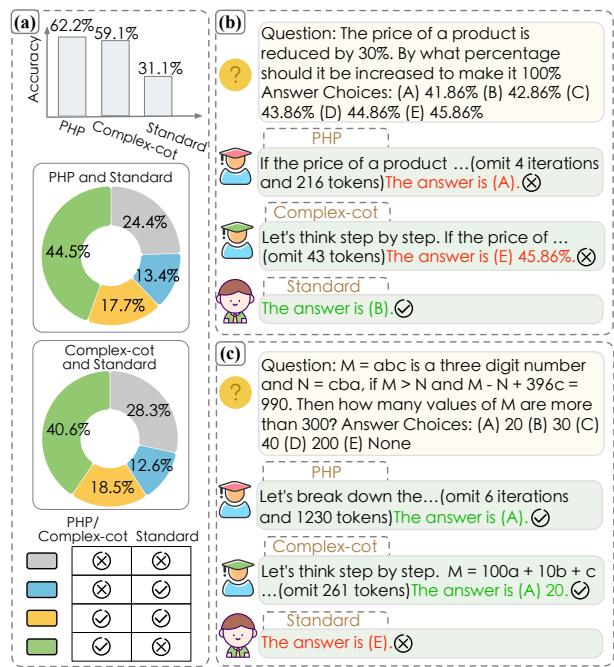
图 1: AQUA 数据集上不同基于 LLM 的推理方法的结果。

在 图 1 (a) 中，你可以看到虽然复杂方法 (如 PHP) 总体表现良好，但有一部分 (13.4% 和 12.6%) 是 Standard (标准/简单) 方法能答对，而复杂方法却失败了的情况。

图 1 (b) 展示了原因: 对于一个简单的百分比问题，复杂模型 (PHP 和 Complex-CoT) 过度分析并弄错了。标准模型则直接给出了答案。相反，在 图 1 (c) 中，难题难住了标准模型，因为它的推理不足，而复杂模型则成功了。

我们需要一种能自适应的方法。我们需要 思维适应 (Adaptation-of-Thought, ADoT) 。

解决方案: 思维适应 (ADoT)

ADoT 的核心思想是动态调整提示的复杂度，以匹配问题的难度。

该方法遵循三个阶段的流程:

  1. 测量问题的难度。
  2. 构建一个包含不同难度级别的演示库。
  3. 检索与当前问题难度相匹配的具体演示。

这是系统的高层架构:

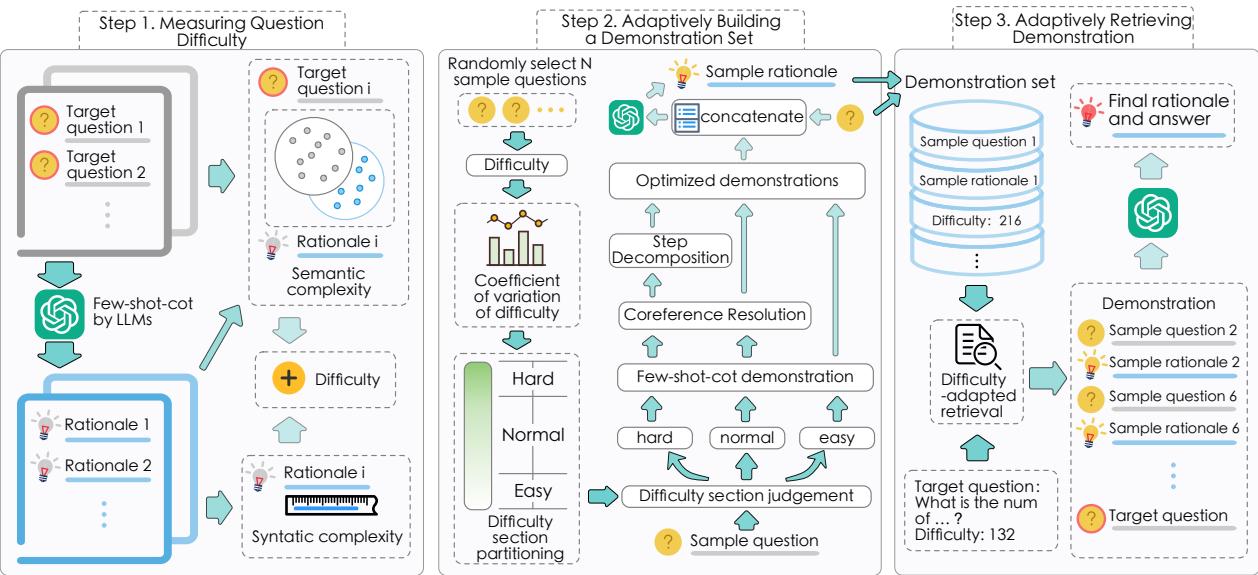
图 2: 我们要提出的 ADoT 方法概览。

让我们分解这三个步骤来理解其机制。

步骤 1: 测量问题难度

如何科学地测量一个问题有多“难”？作者认为，难度不仅仅关于问题文本，还关于解决它所需的推理过程 (rationale) 。

他们使用两个指标来量化难度: 句法复杂性和语义复杂性 。

1. 句法复杂性 (Syntactic Complexity) 这衡量了形式的复杂程度。通常，推理链越长，表明问题越难。他们简单地通过推理过程 (\(r_i\)) 的长度来测量这一点:

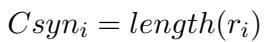
句法复杂性公式

2. 语义复杂性 (Semantic Complexity) 这衡量了知识鸿沟。如果解决方案需要引入大量问题本身未包含的外部知识或概念，那么这个问题就是“难”的。他们通过计算推理过程中出现的、但未在问题 (\(q_i\)) 中出现的非重复“语义词” (名词、动词等) 的数量来计算这一点:

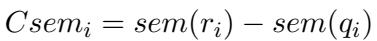
语义复杂性公式

3. 综合难度 (Comprehensive Difficulty) 总难度分数 (\(d_i\)) 是这两个指标的总和。这给出了一个代表解决问题所需努力程度的单一数值。

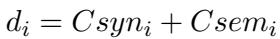
综合难度公式

步骤 2: 自适应地构建演示集

现在系统知道如何测量难度了，它需要一个示例库来展示给 LLM。你不能只使用随机示例；你需要高质量的示例，范围从“简单”到“困难”。

研究人员选取一组样本问题，并根据步骤 1 中计算的难度分数对它们进行分类。为了确定简单、正常和困难的阈值，他们使用变异系数 (coefficient of variation, \(v\)) 来观察难度分数的分布情况:

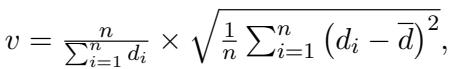
变异系数公式

基于这种分布，他们将问题分为三类。但他们并没有止步于此。他们优化了解决方案的文本，使其成为 LLM 更好的教学工具。

  • 对于“简单”问题: 他们保留标准的思维链演示。
  • 对于“正常”问题: 他们应用指代消解 (Coreference Resolution) 。 这将代词 (他、她、它) 替换为它们实际指代的名词。这减少了歧义，使 LLM 更容易跟随逻辑。
  • 对于“困难”问题: 他们同时应用指代消解和步骤分解 (Step Decomposition) 。

什么是步骤分解? 难题通常包含让模型困惑的逻辑“跳跃”。步骤分解将单一的复杂推理步骤分解为更小的、显式的桥梁。

表 1: 步骤分解案例。

如 表 1 所示，添加一个中间步骤 (在代入之前显式计算 \(b\)) 使逻辑变得无可辩驳。通过给 LLM 喂送这些“超级清晰”的困难示例，模型学会了在面对难题时一丝不苟。

步骤 3: 自适应地检索演示

我们现在有了目标问题的难度分数和一个优化的示例库 (简单、正常、困难) 。拼图的最后一块是检索机制。

当一个新问题进来时，系统会预测其难度。然后，它从库中检索 \(M\) 个与目标问题具有最接近难度分数的演示。

如果问题很难，提示中就会充满复杂的、经过步骤分解的推理示例。如果问题很简单，提示则包含简明、直接的推理。这解决了引言中指出的错配问题。

实验结果

ADoT 真的有效吗？研究人员在涵盖算术、符号和常识推理的 10 个数据集上，将其与 13 个基线方法 (包括 Zero-Shot, Auto-CoT 和 PHP) 进行了测试。

不同难度级别下的表现

最有说服力的结果是 ADoT 与基线方法在不同难度区间的表现对比。

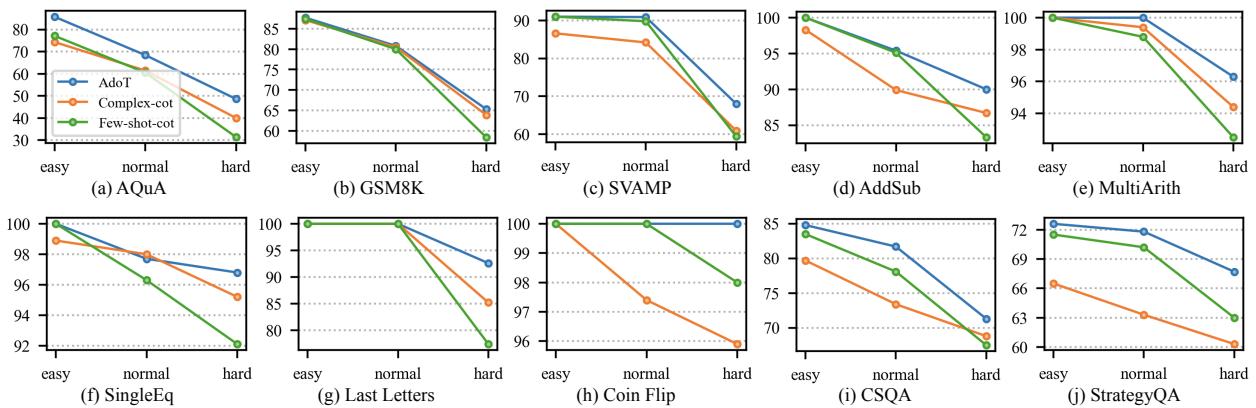
图 3: 不同难度部分的准确率 (%)。

在 图 3 中，请看蓝线 (ADoT) 。

  • 简单问题: ADoT 的表现几乎与简单方法 (Few-shot-cot，绿线) 一样好或更好，避免了“过度思考”的陷阱。
  • 困难问题: ADoT 匹配或击败了复杂方法 (Complex-cot，橙线) ，提供了必要的深度。
  • 稳定性: 与随难度剧烈波动的基线不同，ADoT 非常稳定。

自适应检索的重要性

批评者可能会问: “匹配难度真的重要吗？如果我们只是随机挑选示例会怎样？”作者通过将他们的难度适应 (Difficulty-adapted) 方法与难度反转 (Difficulty-reversed) 方法 (给难题提供简单示例，反之亦然) 以及随机 (Random) 方法进行比较来测试这一点。

图 4: 不同检索方法的准确率 (%)。

图 4 中的结果非常明显。蓝色柱状图 (难度适应) 始终最高。橙色柱状图 (难度反转) 通常最低。这实证表明，问题难度与提示复杂度之间的错配是 LLM 推理错误的主要原因。

消融实验: 哪些组件是关键？

研究人员还将模型拆解，看看哪些部分在驱动成功。

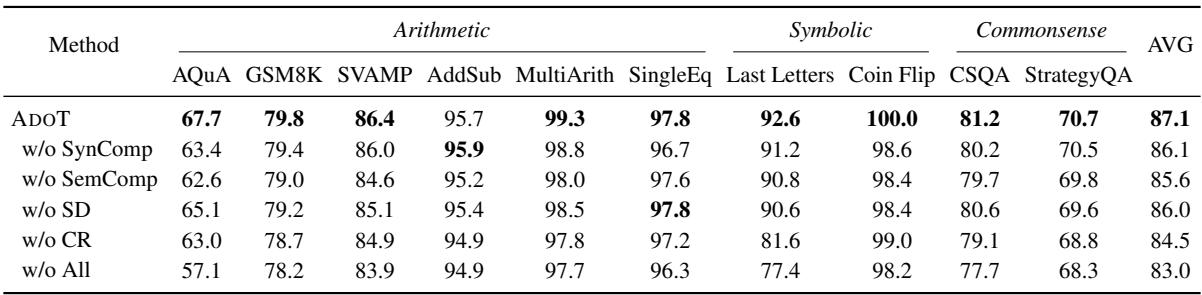
表 3: 消融实验结果。

  • w/o SynComp / SemComp (去除句法/语义复杂性) : 去除句法或语义复杂性度量都会导致性能下降。有趣的是，去除语义复杂性 (知识) 比去除句法复杂性 (长度) 带来的损害更大，这表明模型知道什么比它写了多少稍微重要一些。
  • w/o SD / CR (去除步骤分解/指代消解) : 去除步骤分解 (SD) 和指代消解 (CR) 也会损害性能。这证实了优化示例的质量 (不仅仅是选择它们) 是至关重要的。

案例研究: 眼见为实

最后，让我们看看实际的文本输出，观察 ADoT 与其他方法相比的行为。

图 6: 案例研究结果。粗体: 句法复杂性。下划线: 语义复杂性。

在 图 6 中:

  • 简单问题 (上) : 复杂模型 (PHP) 尝试迭代 4 次并写了 208 个 token，最终得到了错误的答案 (A)。标准模型仅用 16 个 token 就正确回答了 (B)。 ADoT 正确地将其识别为简单问题，使用简短的推理路径 (17 个 token) ，并答对了 (B)。
  • 困难问题 (下) : 标准模型几乎没有尝试 (0 个推理 token) 并失败了。复杂模型 (PHP) 写了一大段文字 (304 个 token) 并答对了。 ADoT 将其识别为困难问题，生成了详细的推理过程 (76 个 token) ，也得到了正确答案 (A)。

结论

“Adaptation-of-Thought” 这篇论文凸显了 LLM 研究的成熟。我们正在从试图寻找解决所有问题的“一个万能提示词”，转向对不同输入进行区别对待的自适应系统 。

通过通过句法和语义复杂性量化难度，并动态调整提供给模型的示例，ADoT 取得了最先进的结果。它提醒我们，在人工智能领域，就像在教学中一样，最好的解释是那些与学生——以及问题——完美契合的解释。