大语言模型 (LLM) 在生成代码、总结历史甚至创作诗歌方面展现出了惊人的能力。然而，当涉及严谨的数学推理——特别是形式化定理证明时，它们往往会碰壁。在形式化数学的世界里，“差不多对”就等于“全错”。一个证明必须在逻辑上无懈可击，步骤分明，并且可以被计算机程序验证。

当标准的 LLM 试图通过直觉猜测下一步来解决这些问题 (这个过程称为正向链/前向推理) 时，人类数学家通常采用不同的工作方式。他们会盯着目标问自己: “为了让这个目标成立，我首先需要证明什么？”这就是所谓的反向链 (Backward Chaining) 或逆向推理 。

在这篇文章中，我们将深入探讨 BC-Prover , 这是由阿里巴巴集团和鹏城实验室的研究人员提出的一个新框架。该论文介绍了一种方法，结合了 LLM 的创造力与结构化的逆向推理策略，用以解决 Lean 编程语言中复杂的数学证明问题。

挑战: 交互式定理证明

交互式定理证明 (Interactive Theorem Proving, ITP) 就像是数学家的电子游戏。你会得到一个初始状态 (假设) 和一个最终 BOSS (需要证明的定理) 。你必须发出指令，称为策略 (tactics) , 来转换状态，直到 BOSS 被击败 (目标被证明) 。

这种环境通常涉及一个证明辅助工具，如 Lean 或 Isabelle 。 这些辅助工具是非常严格的编译器，会拒绝任何不遵循逻辑规则的步骤。

“仅正向推理”的问题

大多数现有的 AI 证明器依赖于正向链 (Forward Chaining) 。 它们观察当前的假设并预测下一个逻辑步骤，希望最终能偶然碰上目标。

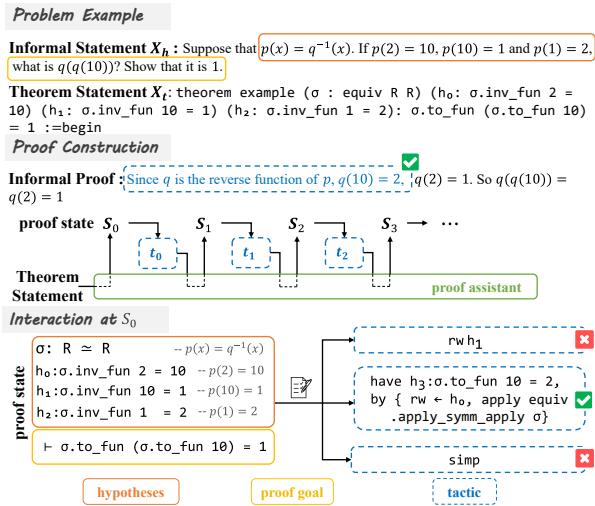
图 1: 问题示例。该图展示了一个非形式化的陈述和证明，随后是在状态 S0 下的形式化交互。它说明了像 ‘rw’ 和 ‘simp’ 这样的正向策略是如何失败的，而反向的 ‘have’ 策略却成功了。

如图 1 所示，证明器从一个非形式化的陈述开始，将其转化为形式化定理。在“Interaction at \(S_0\)” (在 \(S_0\) 处的交互) 部分，我们可以看到它的挣扎。目标是证明函数 \(\sigma\) 的一个特定值。

  • 证明器尝试使用假设 \(h_1\) 进行 rw (重写) 。 失败。
  • 它尝试 simp (简化) 。 失败。
  • 然而，一种反向策略奏效了。通过观察目标，证明器意识到它首先需要证明一个子目标 (\(h_3\)) 。这对应于非形式化证明中的彩色句子: “由于 q 是 p 的反函数……”

标准的 LLM 经常会迷失方向，因为可能的正向步骤搜索空间是无限的。如果没有计划，它们就会漫无目的地游荡。

BC-Prover 登场: 一个策略性框架

作者提出了 BC-Prover , 这是一个不仅猜测下一步，而且会规划路线的框架。它优先考虑伪步骤 (pseudo steps) ——即证明的中间、结构化草图——并使用它们来指导严谨的形式化证明过程。

架构

BC-Prover 的工作流程主要分为两个阶段: 伪步骤生成和证明构造 。

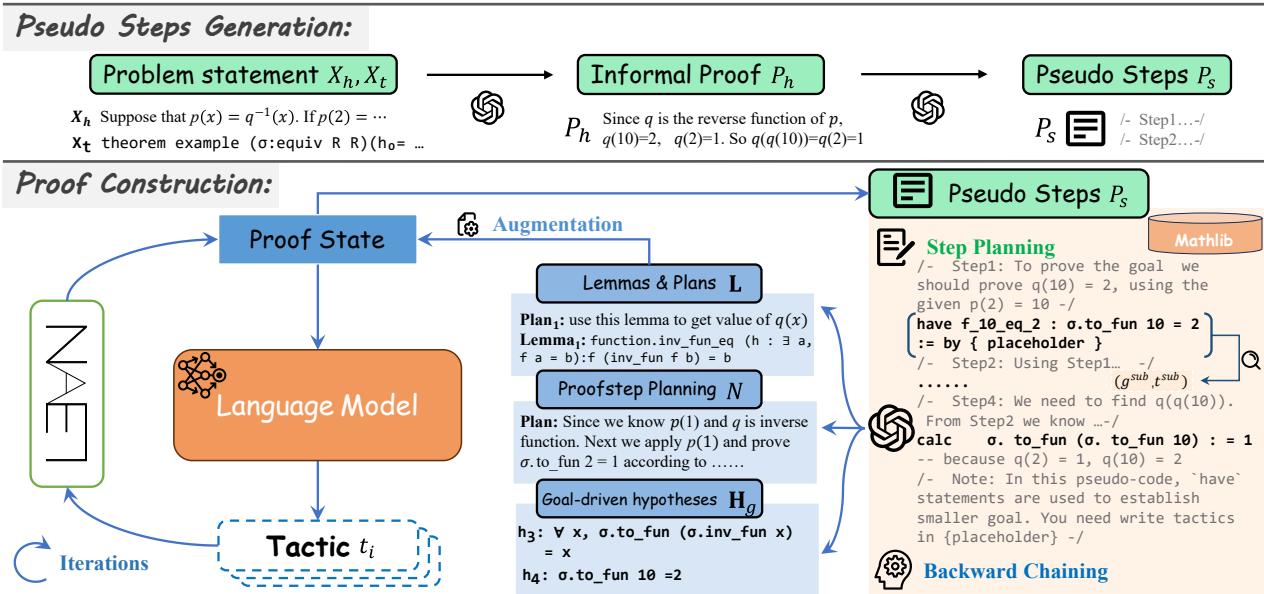
图 2: BC-Prover 概览。顶部展示了从问题陈述生成伪步骤的过程。底部展示了涉及反向链、步骤规划和策略生成的迭代证明构造循环。

如图 2 所示，该过程首先获取问题陈述 (\(X_h, X_t\)) 并生成非形式化证明。然后将其细化为伪步骤 (\(P_s\)) ——即证明应该如何进行的高级算法。

一旦伪步骤准备就绪，与 Lean 证明辅助工具的实际交互就开始了。这不仅仅是一个简单的循环；它涉及三个复杂的组件:

  1. 反向链 (Backward Chaining) : 将目标分解为子目标。
  2. 步骤规划 (Step Planning) : 决定究竟如何实施下一步。
  3. 策略生成 (Tactic Generation) : 编写实际的 Lean 代码。

让我们分解这些组件背后的数学和逻辑。

1. 伪步骤生成 (Pseudo Steps Generation)

在编写代码之前，程序员通常会写伪代码。同样，BC-Prover 首先将数学问题转化为非形式化证明 (\(P_h\)) ，然后再转化为结构化的伪步骤 (\(P_s\)) 。

\[ \begin{array} { c } { { \mathcal { M } : ( X _ { t } , X _ { h } ) \rightarrow P _ { h } } } \\ { { \mathcal { M } : ( X _ { t } , X _ { h } , P _ { h } ) \rightarrow P _ { s } } } \end{array} \]

这里，\(\mathcal{M}\) 代表大语言模型。通过强制模型清晰地表达计划 (\(P_s\)) ，系统减少了 LLM “产生幻觉”并编造不存在路径的可能性。

2. 反向链 (Backward Chaining)

这是论文的核心贡献。在证明的每次迭代中，BC-Prover 都会查看当前的伪步骤 (\(P_s\)) 和当前状态 (\(S_i\)) ，以确定是否应该进行逆向工作。

它使用 LLM 来识别子目标 (\(g^{sub}\)) 以及证明它们所需的策略 (\(t^{sub}\)) 。

\[ \mathcal { M } : ( P _ { s } , S _ { i } ) \rightarrow \mathbf { H } \]

输出 \(\mathbf{H}\) 是一组潜在的子目标。然后系统会要求 Lean 证明辅助工具验证这些子目标。如果有效，它们将被添加到“目标驱动假设” (Goal-Driven Hypotheses, \(\mathbf{H}_g\)) 列表中。

\[ { \mathbf { H } } _ { g } = \operatorname { L e a n } ( { \mathbf { H } } , S _ { i } ) \]

最后，证明状态被增强了。AI 现在不仅知道什么是真的 (现有的假设) ，还知道需要什么成真才能完成任务。

\[ S _ { i } ^ { \theta } = [ S _ { i } , \mathbf { H } _ { g } ] \]

这极大地缩小了搜索空间。代理不再搜索“任何有效的数学移动”，而是搜索“能证明这个特定子目标的移动”。

3. 步骤规划与检索 (Step Planning & Retrieval)

形式化证明通常需要来自庞大库 (如 Lean 的 mathlib) 中的特定引理。LLM 无法完美地记住每一个引理。

BC-Prover 采用了一个步骤规划模块。它首先用自然语言 (\(D\)) 描述当前的增强状态 (\(S_i^\theta\)) ，然后规划下一步行动 (\(N\)) 。

\[ \begin{array} { c } { { \mathcal { M } : S _ { i } ^ { \theta } \rightarrow D } } \\ { { \mathcal { M } : ( D , S _ { i } ^ { \theta } , P _ { s } ) \rightarrow N } } \end{array} \]

同时，它使用检索器从库中查找相关引理 (\(\mathbf{L}_r\)) ，并使用 LLM 选择最有用的引理 (\(\mathbf{L}\)) 。

\[ \mathcal { M } : ( \mathbf { L } _ { r } , S _ { i } ^ { \theta } , P _ { s } ) \rightarrow \mathbf { L } \]

4. 证明步骤生成器 (The Proofstep Generator)

最后，所有这些丰富的信息——当前状态、反向链子目标、步骤计划和检索到的引理——都被输入到生成器中。

\[ \begin{array} { c } { S _ { i } ^ { * } = [ S _ { i } ^ { \theta } , N , \mathbf { L } ] } \\ { \mathcal { M } : ( S _ { i } ^ { * } ) \rightarrow \{ t _ { i } ^ { 0 } , . . . , t _ { i } ^ { k } \} } \end{array} \]

模型输出一组候选策略 (\(t_i\)) ，然后在 Lean 中执行这些策略，看看哪一个能正确推进证明。

\[ S _ { j } = \mathrm { L e a n } ( t _ { j - 1 } ^ { ' } , S _ { j - 1 } ) \]

实验结果

研究人员在 miniF2F 上评估了 BC-Prover，这是形式化奥林匹克级数学竞赛的标准基准。他们将其与包括纯 GPT-4、ReProver 和 LLMStep 在内的几个基线进行了比较。

基准测试性能

结果非常显著。与基线相比，BC-Prover 实现了高得多的“Pass@1”率 (一次尝试解决问题) 。

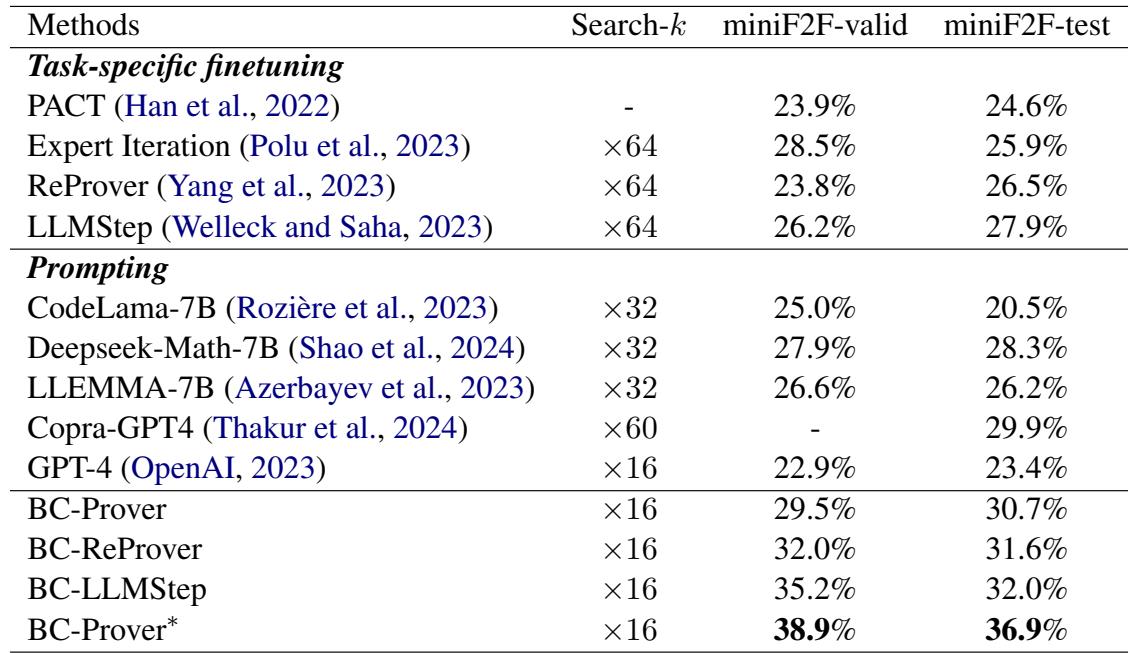
表 1: miniF2F 基准测试的 Pass@1 结果。表格显示 BC-Prover 在测试集上达到了 30.7%，优于 GPT-4 (23.4%) 和标准 CodeLama (20.5%)。

如表 1 所示, BC-Prover 在 miniF2F-test 上达到了 30.7% , 优于 GPT-4 (23.4%)，并显著击败了其他提示方法。

也许更令人印象深刻的是协作设置 (Collaborative Setting) 。 当 BC-Prover 的逻辑与 ReProver 等特定任务模型结合时 (创建“BC-ReProver”) ，性能提升更高。这表明反向链框架是“即插即用”的——它可以增强现有的模型。

反向链真的发生了吗？

人们可能会想，模型是真的在进行逆向推理，还是仅仅运气好。研究人员分析了模型生成的策略类型。

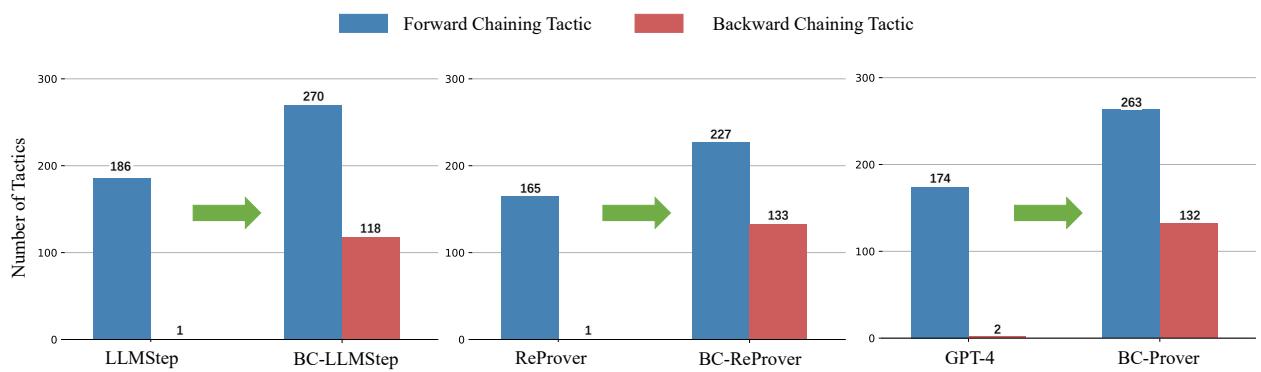
图 3: 比较正向与反向链策略数量的柱状图。与 LLMStep 或 GPT-4 等基线模型相比，BC-Prover 显示出反向链策略的大幅增加。

图 3 证实了这一假设。像 LLMStep 和 GPT-4 这样的标准模型几乎完全依赖正向链 (蓝色条) 。BC-Prover (及其协作变体) 生成了大量的反向链策略 (红色条) 。这种结构性转变表明，模型正在积极地分解目标，而不仅仅是对假设做出反应。

搜索效率

规划的一个主要优势是效率。如果你知道要去哪里，你就不会走那么多弯路。

作者比较了 GPT-4 与 BC-Prover 的搜索树。

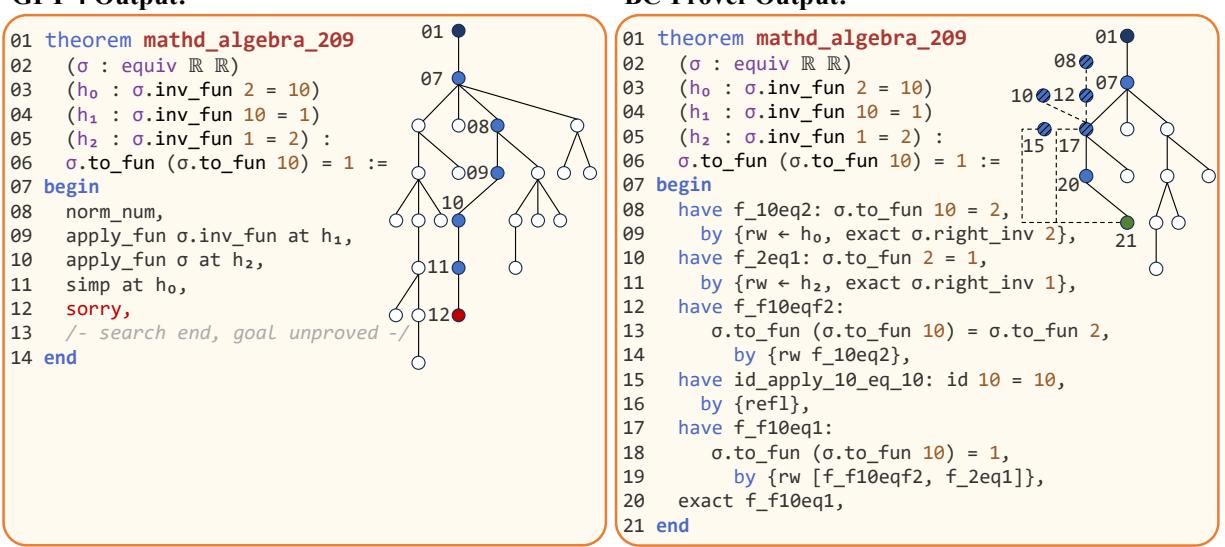
图 4: 定理 mathd_algebra_209 的搜索树对比。左侧显示 GPT-4 探索了一个很深的失败分支 (红色节点) 。右侧显示 BC-Prover 使用更短的反向链路径 (绿色勾选) 成功找到了证明。

在图 4 中，我们可以看到 mathd_algebra_209 的证明过程可视化。

  • 左侧 (GPT-4): 模型漫无目的地重写假设。它将方程转化为看起来复杂但没有帮助的形式。它在 25 次迭代后进入了死胡同 (红色节点 12) 。
  • 右侧 (BC-Prover): 模型使用反向链 (虚线) 。它建立了一个连接假设与目标的子目标 (第 08-09 行) 。它用更少的步骤和更少的总迭代次数找到了解决方案。

效率数据加强了这一点:

表 3: 效率分析。BC-Prover 的平均证明步骤长度为 1.80，最大迭代次数为 23，相比之下 GPT-4 的平均证明步骤为 2.07，最大迭代次数为 61。

BC-Prover 以更短的证明 (Avg.P 1.80) 和极少的搜索迭代 (Max.I 23 vs 61) 解决了问题，同时节省了时间和计算成本。

为什么这很重要

BC-Prover 的成功凸显了当前生成式 AI 的一个关键局限性: 正向预测并不等同于推理。

通过简单地预测下一个 token 或下一行代码，AI 往往缺乏“大局观”。BC-Prover 强迫 AI 采用类似人类的策略:

  1. 起草计划 (伪步骤) 。
  2. 从解决方案逆向推导 (反向链) 。
  3. 频繁验证 (与 Lean 交互) 。

消融实验 (Ablation Study)

为了证明系统的每个部分都很重要，作者进行了消融研究，逐一移除组件。

表 2: 消融研究。移除反向链 (w/o BC) 导致验证集上的性能从 29.5% 下降到 25.4%。移除步骤规划 (w/o SP) 则下降到 27.4%。

表 2 显示，移除反向链 (w/o BC) 导致性能急剧下降 (~4-5%) 。移除步骤规划 (w/o SP) 也会损害性能。这两种机制对于框架的成功都是必不可少的。

结论

BC-Prover 代表了自动推理领域的重要一步。它摆脱了寄希望于 LLM 凭直觉给出答案的“黑盒”方法，转向了一种神经符号 (neuro-symbolic) 方法，即由结构化逻辑和形式化验证来指导 LLM。

对于 AI 领域的学生和研究人员来说，结论很清楚: LLM 是强大的引擎，但它们需要方向盘。像反向链和显式规划这样的技术提供了这种控制力，使我们能够解决以前无法触及的严谨数学问题。

该领域的未来工作可能会集中在提高生成的子目标的质量上。正如论文中所指出的，虽然 BC-Prover 生成了许多有用的假设，但它也生成了一些微不足道的假设 (论文中的图 12) 。改进这种“数学直觉”可能会使 AI 系统成为科学发现中真正的合作伙伴。