大型语言模型 (LLM) 的规模正在爆炸式增长。从 GPT-4 到 Llama，模型变得越来越大，越来越聪明，但关键是——运行成本也越来越高。造成这种成本的主要罪魁祸首是这些架构的稠密 (dense) 特性: 每当你问一个问题，模型中的每一个参数都会被激活来计算答案。

想象一个图书馆，为了回答一个问题，图书管理员必须打开并阅读书架上的每一本书。这就是稠密模型。

一个更高效的替代方案是混合专家 (Mixture-of-Experts, MoE) 架构。在 MoE 中，模型被划分为称为“专家”的专门子网络。对于任何给定的输入，模型只激活这些专家中的极小一部分。这就像图书管理员确切地知道哪三本书包含答案，并忽略其余的书。

然而，这里有个陷阱。从头开始训练 MoE 是不稳定且困难的。一种称为 “MoEfication” (MoE化) 的巧妙变通方法允许我们将标准的、预训练的稠密模型转换为 MoE，而无需昂贵的重新训练。直到最近，这种方法仅对使用 ReLU 激活函数的模型有效。

在这篇文章中，我们将深入探讨一篇解决了这个问题的研究论文: “Breaking ReLU Barrier: Generalized MoEfication for Dense Pretrained Models” (打破 ReLU 壁垒: 面向稠密预训练模型的通用 MoE 化) 。 我们将探索作者如何开发 G-MoEfication , 这是一种允许将任意稠密模型 (使用 GeLU, SiLU 等) 转换为高效、稀疏的混合专家模型的技术。

问题所在: ReLU 与 GeLU 的鸿沟

要理解为什么转换模型很难，我们需要先了解激活函数 。 这些是神经网络内部的数学门控，决定神经元是否“被激发”。

多年来, ReLU (线性整流单元) 一直是标准。ReLU 非常简单: 如果一个值是负的，它就变成零。如果是正的，它保持不变。

\[ \text{ReLU}(x) = \max(0, x) \]

因为 ReLU 强制所有负值完全为零，所以基于 ReLU 的神经网络天然是稀疏的 。 许多神经元自然输出为零。这使得我们可以很容易地将它们切断 (关闭) ，而不会太大地改变模型的输出。

然而，现代 LLM (如 BERT, GPT, Llama 和 Phi) 很少再使用 ReLU。它们使用更平滑的变体，如 GeLU (高斯误差线性单元) 或 SiLU 。 这些函数对训练稳定性更好，但对我们的目的来说有一个主要的缺点: 它们几乎从未完全为零。

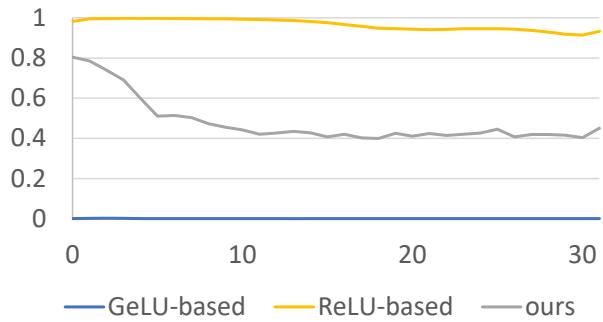
图 1: GeLU 与 ReLU 模型的稀疏性趋势。

如图 1 所示，橙色线代表基于 ReLU 的模型，它保持了高稀疏性 (很多零) 。蓝色线代表基于 GeLU 的模型 (Phi-2) ，其实际稀疏性几乎为零。

如果你试图通过将小数值视为零来“MoE化”一个 GeLU 模型，你会破坏信息，模型的性能也会随之崩溃。这就是 ReLU 壁垒 。

背景: 什么是 MoEfication？

在看解决方案之前，让我们简要了解一下我们最初是如何将稠密模型转换为 MoE 的。

Transformer 中的标准前馈网络 (FFN) 层看起来像这样:

  1. 输入进入。
  2. 乘以权重 (\(W_1\)) 。
  3. 应用激活函数 (\(\sigma\)) 。
  4. 乘以输出权重 (\(W_2\)) 。

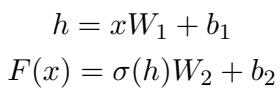
标准 FFN 与 MoE 的方程。

在 MoEfication 中，目标是将 FFN 层中的神经元分成组，即“专家”。

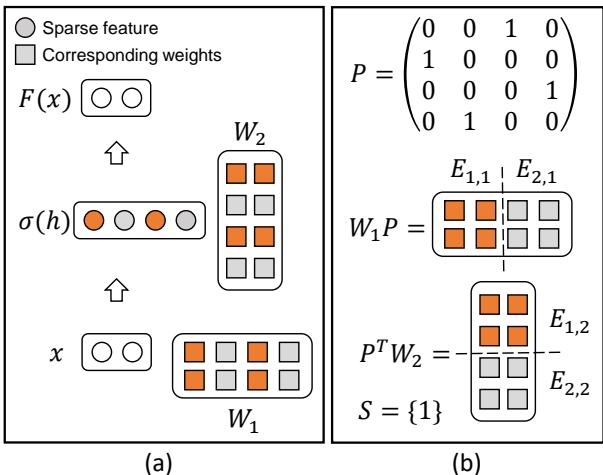
图 2: 将神经元聚类为专家。

如图 2 所示，我们要寻找倾向于同时被激发的神经元 (图 a 中的橙色点) 并将它们聚类在一起。

  • 面板 (a) 展示了稀疏激活 (ReLU) 如何让许多神经元处于未激活状态 (灰色) 。
  • 面板 (b) 展示了我们如何将这些权重分组成簇。

在数学上，我们将大型权重矩阵分解为较小的“专家”矩阵 (\(E_{i,1}, E_{i,2}\)) 。在推理过程中，一个“路由器”只选择最相关的专家 (\(S\)) 来处理输入。

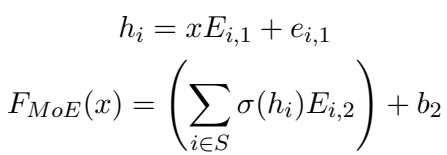
MoE 公式方程。

上面的公式描述了 MoE 的输出。我们不再对所有神经元求和，而是只对集合 \(S\) 中被选中的专家求和。

核心方法: G-MoEfication

研究人员提出了 G-MoEfication (通用 MoE 化) 来处理激活函数并非天然稀疏的模型。他们面临一个两难境地:

  1. 如果你将未被选中的专家视为零 (就像在标准 MoE 中那样) ，你会丢失包含在那些小的、非零 GeLU 激活值中的信息。
  2. 如果你继续计算它们，你就没有节省任何计算成本。

解决方案需要三个巧妙的步骤: 软稀疏性 (Soft Sparsity) 、代表值 (Representative Values) 和静态嵌入 (Static Embeddings) 。

1. 重新定义稀疏性

作者不再寻找“硬”零，而是定义了“软稀疏性”。如果激活值落在零周围的一个非常小的范围 (\(-\epsilon\) 到 \(+\epsilon\)) 内，他们就认为它是稀疏的。

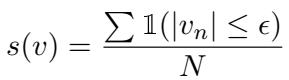
软稀疏性方程。

这允许我们将 GeLU 模型视为具有“稀疏”区域，前提是我们能有效地处理小的残差。

2. 代表值技巧

这是关键的创新点。在标准 MoE 中，如果一个专家未被选中，它的贡献被设为 0。 在 G-MoEfication 中，如果一个专家未被选中，它的贡献被设为一个 代表值 (\(r\)) 。

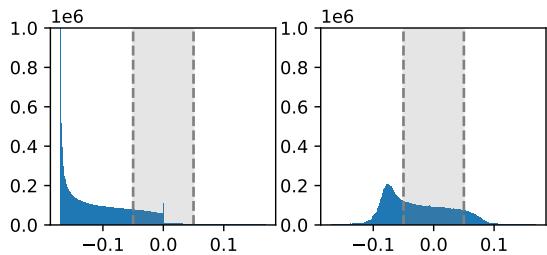
图 4: 使用代表值移动分布。

看一看 图 4 。

  • 左侧: GeLU 模型中激活值的原始分布。它在零附近出现峰值，但并不完全是零。
  • 右侧: 作者建议移动分布。他们为每个神经元确定一个“代表值” (通常是均值) 。

通过减去这个代表值，“残差” (剩余部分) 变得更接近于零。这最大限度地减少了当我们忽略未被选中专家的具体波动时的误差。

优化目标从简单地最小化将专家归零的误差，变为最小化用代表值替换它们的误差:

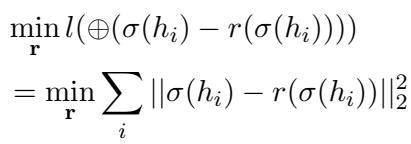
最小化残差误差的方程。

最佳代表值 \(r\) 结果很简单: 就是该神经元在样本数据集上的平均激活值 。

3. 计算捷径 (静态嵌入)

你可能会想: “等等，如果我们必须为每个未被选中的专家添加一个代表值，我们岂不是还在为每个专家做数学运算？这怎么能节省时间呢？”

如果我们天真地计算每个未选中专家的代表值贡献，它看起来就像下面的图 3(b)——计算量很大。

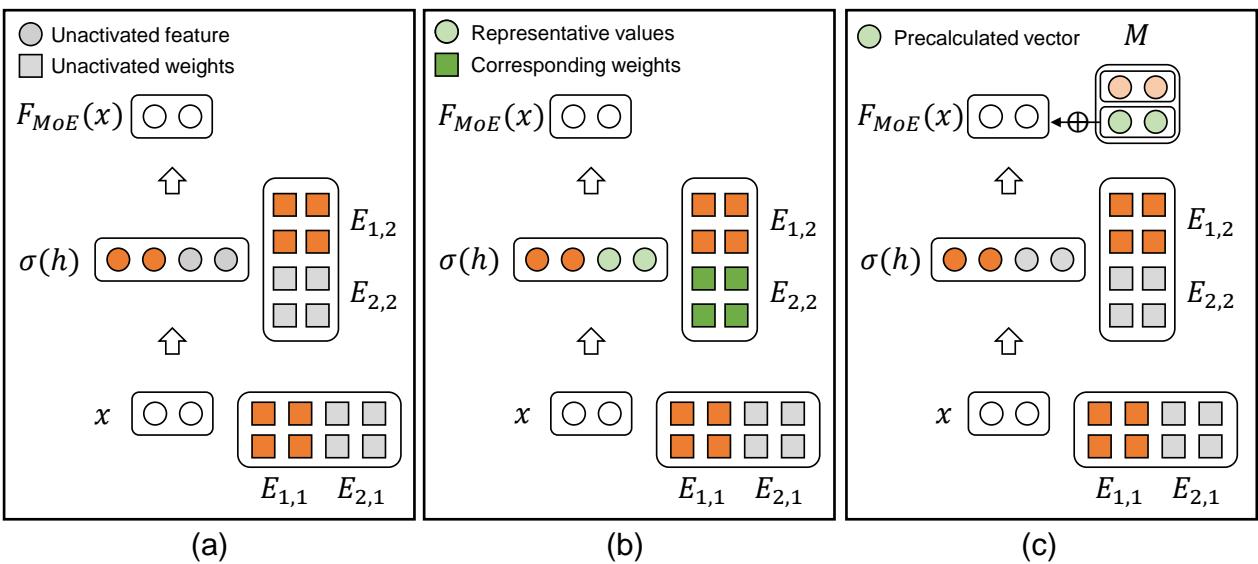
图 3: 从朴素 MoE 到预计算嵌入的演变。

  • 图 3(a): 朴素 MoE 直接丢弃信息 (灰点) 。虽然快，但对 GeLU 来说不准确。
  • 图 3(b): 保留代表值 (绿点) 保存了信息，但需要计算。
  • 图 3(c) - 解决方案: 因为代表值 \(r\) 是静态的 (它只是均值，不会随输入变化) ，所以它通过第二层权重 (\(W_2\)) 传递的结果也是恒定的！

研究人员预先计算了所有代表值的输出。他们将这些加总成一个单一的向量 (或嵌入) 。

在推理过程中，方程变为:

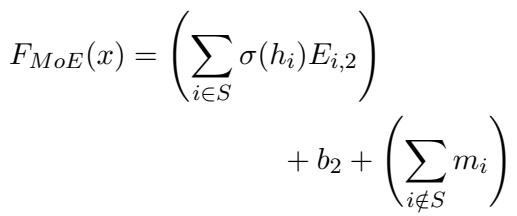
最终高效的 MoE 方程。

这里:

  • 第一项 \(\sum_{i \in S} \dots\) 是对少数被选中的专家的标准计算。
  • 项 \(\sum_{i \notin S} m_i\) 代表未被选中专家的贡献。因为 \(m_i\) 是预先计算好的，这只是一个简单的向量加法。

这个聪明的技巧允许模型“虚拟出”未被选中专家的存在，而无需实际对它们进行繁重的矩阵乘法。

实验与结果

这个理论在实践中站得住脚吗？研究人员在多个模型上测试了 G-MoEfication，包括 mBERT (多语言 BERT) 、SantaCoder、Phi-2 和 Falcon-7B 。

在 mBERT 上的表现

他们在 42 种语言的命名实体识别 (NER) 和词性标注 (POS) 任务上，将 G-MoEfication 与标准 MoEfication (假设硬稀疏性) 进行了比较。

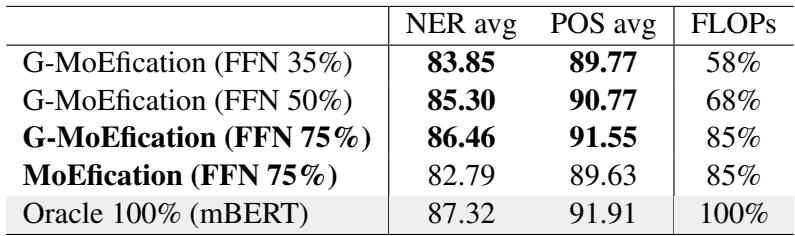
表 1: mBERT 性能比较。

表 1 显示了结果:

  • G-MoEfication (FFN 35%) 保留了原始模型约 96-97% 的性能，同时仅使用了 58% 的 FLOPs (计算操作) 。
  • 至关重要的是，看第一列 (NER avg) ，G-MoEfication 得分 83.85 , 显著击败了标准 MoEfication 的 82.79 , 即使标准版本使用了更多的参数 (75%) 。

生成模型 (零样本)

MoEfication 的一个主要担忧是它是否会破坏生成模型微妙的能力。作者将他们的方法应用于 Phi-2 和 Falcon-7B , 没有任何微调 (零样本评估) 。

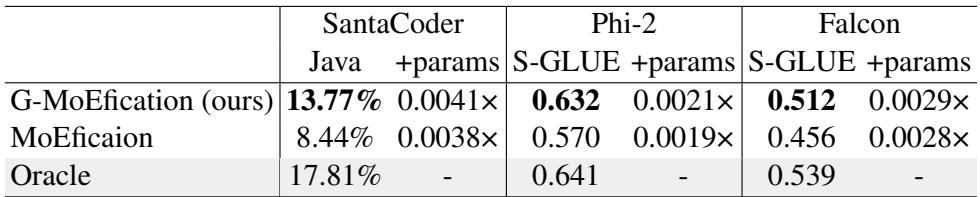
表 2: 生成模型上的性能。

如表 2 所示:

  • Phi-2: 原始模型在 SuperGLUE 上得分为 0.641。G-MoEfication 达到 0.632——下降可以忽略不计。标准 MoEfication 显著下降至 0.570。
  • SantaCoder: 在代码生成 (Java) 上，G-MoEfication 达到 13.77% , 远超标准 MoEfication 的 8.44%。

可视化专家

MoE 的一个迷人方面是“专家专业化”。特定的专家真的能学到特定的概念吗？

研究人员可视化了多语言 mBERT 模型的专家选择模式。

图 5: 按语言的专家选择 UMAP 投影。

图 5 投影了 103 种不同语言的专家使用模式。颜色代表语系 (例如，日耳曼语族、罗曼语族、斯拉夫语族) 。聚类清晰可见: 模型自动将法语、西班牙语和意大利语路由到相似的专家，而将中文和日语路由到其他专家。这证实了 MoEfication 过程保留了稠密模型的语义结构。

计算效率

最后，值得验证一下“静态向量”技巧是否真的节省了时间。

表 3 (如下) 比较了参数选择方法。

表 3: 选择方法的比较。

该表显示，他们训练的专家选择优于随机选择和剪枝 (SNIP) 。此外，论文指出，使用静态向量设计将 FLOPs 减少到原始 mBERT 的 58% 。 如果没有静态向量技巧 (即时计算代表值) ，FLOPs 实际上会增加到 101%。预计算是至关重要的。

结论与启示

“ReLU 壁垒”长期以来阻碍了现代、稠密 Transformer 作为混合专家模型的高效部署。G-MoEfication 为这个问题提供了一个优雅的数学解决方案。

通过认识到“归零”并不是节省计算的唯一方法，并利用存储为静态嵌入的代表值 , 作者解锁了一条压缩和加速几乎所有现代 LLM 的路径。

主要收获:

  1. 通用方法: 适用于 GeLU, SiLU 和其他非稀疏激活函数。
  2. 无需预训练: 直接转换现有的检查点。
  3. 保留信息: 使用均值统计来近似未被选中的专家，而不是删除它们。
  4. 高效率: 将繁重的矩阵数学转换为轻量级的向量加法。

随着模型持续增长，像 G-MoEfication 这样的技术对于使它们在标准硬件上更易访问、更快速和更环保至关重要。