当我们想到大型语言模型 (LLMs) ，如 LLaMA 或 GPT-4 时，通常会认为它们是语言大师。它们能写诗、总结邮件以及调试代码。但在核心层面，这些模型是序列预测器——它们观察一系列 token，并预测接下来会出现什么。

这引发了一个有趣的问题: 如果序列不是文本，而是来自物理系统的数据，LLM 能否仅仅通过观察数字就学会物理定律?

在最近的一篇论文中，来自康奈尔大学和伦敦帝国理工学院的研究人员探索了正是这个问题。他们发现，LLM 确实可以“学习”动力系统的支配原则——从混沌的天气模型到随机的股票市场波动——且无需任何微调。更令人印象深刻的是，他们发现随着模型看到的数据增多，其理解这些系统的能力会在数学层面上得到提升，从而揭示了一种新型的上下文神经缩放定律 (In-Context Neural Scaling Law) 。

在这篇文章中，我们将拆解这项研究，解释用于从文本模型中提取数学信息的巧妙算法“Hierarchy-PDF”，并可视化 LLM 如何学会模拟世界。

前提: 从文本到轨迹

要理解这项研究的分量，我们首先需要定义问题。动力系统是描述事物随时间变化的数学规则。它们可以是:

  1. 随机的 (Stochastic) : 涉及随机性 (例如粒子的布朗运动) 。
  2. 确定性的 (Deterministic) : 没有随机性，但可能很复杂 (例如用于天气建模的 Lorenz 系统) 。
  3. 混沌的 (Chaotic) : 确定性但对初始条件高度敏感。

研究人员想知道，预训练的 LLM (特别是 LLaMA-13b) 能否仅仅通过上下文，观察这些系统的数字序列并找出底层的公式——即“转换规则”。

“零样本”挑战

通常，当我们使用机器学习进行时间序列分析时，我们会针对该数据训练一个特定的模型。在这里，研究人员没有训练模型。他们只是将一串数字 (像文本一样标记化) 输入到 LLM 中，并要求它预测下一个状态。

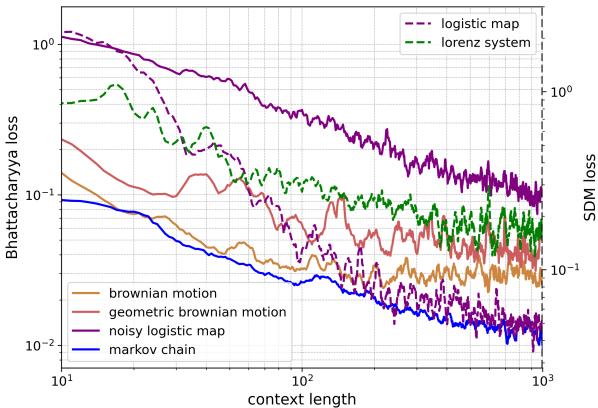
Figure 1: Evolution of the loss function for the predicted next state by LLaMA-13b with respect to the number of observed states in various physical systems.

如上方的 图 1 所示，结果令人震惊。图表显示，随着模型看到的数据 (上下文长度) 增加，错误率 (损失) 在下降。无论是布朗运动的随机游走 (实线橙色) 还是 Lorenz 系统的混沌行为 (虚线绿色) ，随着 LLM 阅读的历史数据增多，它预测物理现象的能力也随之增强。

方法论: 从语言模型中提取数学

如何让语言模型输出连续数字的精确概率分布？LLM 输出的是像“apple”、“code”或“7”这样的 token 的 logits (分数) 。它天生并不会输出连续的概率密度函数 (PDF) 。

为了解决这个问题，研究人员开发了一个名为 Hierarchy-PDF 的框架。

1. 将物理现象标记化 (Tokenizing)

首先，时间序列数据——即浮点数——必须转换为文本。研究人员将数据重新缩放到一个固定区间，并将数字表示为数字字符串。例如，一个值可能被表示为 3 位数字序列。

假设系统遵循马尔可夫转换规则。这意味着下一个状态的概率取决于当前状态:

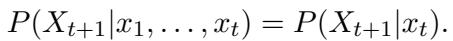
Equation describing Markov property

2. Hierarchy-PDF 算法

这是该论文的核心创新。由于 LLM 一次预测一个 token，因此预测像 5.23 这样的数字是一个分层的过程。

  1. 粗略分箱 (Coarse Binning) : 模型预测第一位数字。如果它给 token “5” 分配了高概率，这意味着该值可能在 5.0 到 6.0 之间。
  2. 精细化 (Refining) : 给定第一位数字是 5，模型预测第二位数字。如果它选择了 “2”，范围就缩小到 [5.20, 5.30]。
  3. 精度 (Precision) : 这个过程持续进行，直到达到所需的位数。

这创建了一个树状结构。通过在每一层查询 LLM 对数字 0-9 的概率，研究人员可以构建一个高度详细的直方图，以此逼近物理系统的连续概率分布。

Figure 3: An example of hierarchical transition rules extracted from LLaMa-13b.

图 3 完美地展示了这一点。“习得的转换规则” (右下角) 不仅仅是单点预测。它们是通过“放大”数字 (按分辨率颜色编码) 构建的完整概率分布。这使得 LLM 能够表达不确定性——这是随机系统的一个关键特征。

3. 离散系统

对于具有离散状态的更简单系统 (如在整数 0-9 之间跳跃的马尔可夫链) ，过程更加直接。模型只需预测下一个 token。

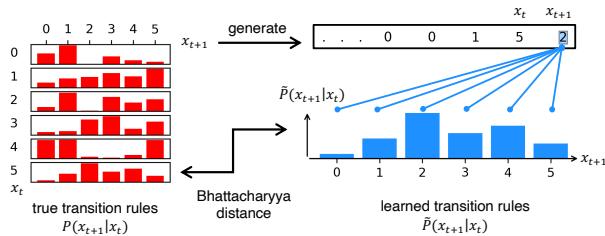
Figure 2: Extracting learned transition rules of systems with discrete state space.

如 图 2 所示，研究人员将“真实”转换矩阵 (系统实际的工作方式) 与从 LLM 的 logits 推导出的“习得”转换矩阵进行了比较。它们的匹配程度惊人地好。

4. 衡量成功: 巴塔查里亚距离 (Bhattacharyya Distance)

为了量化 LLM 学习物理的效果，研究人员需要一个指标来比较两个概率分布: 真实分布 (源自数学方程) 和预测分布 (从 LLM 中提取) 。

他们选择了 巴塔查里亚距离 。

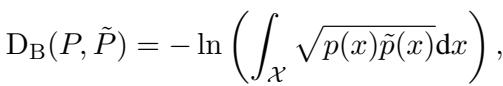
Equation for Bhattacharyya distance

简而言之，这衡量了两个统计总体的重叠程度。如果 LLM 预测的概率“云”与物理方程的现实完美重叠，则距离为零。

实验: 动力系统大观

研究人员在多种系统上测试了 LLaMA-13b，以观察它是在死记硬背数字还是真的在学习规则。

案例 1: 离散马尔可夫链

他们从随机生成的马尔可夫链开始。这是一个下一个状态完全由矩阵中定义的概率决定的系统:

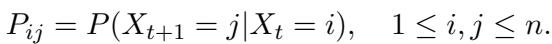
Equation for Markov transition matrix

因为矩阵是随机的，LLM 无法依赖预训练知识。它必须查看上下文窗口来找出概率。

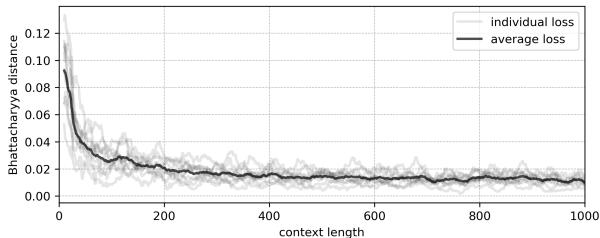
Figure 4: Markov chain in-context loss curves decay rapidly.

图 4 显示了结果。巴塔查里亚距离 (误差) 迅速下降。当上下文长度为零时，模型一无所知。但当它看到链条的 100 或 200 步时，它逆向工程出了创建数据的随机矩阵。

案例 2: 随机系统 (布朗运动)

接下来，他们转向连续随机过程。经典的例子是布朗运动——悬浮在流体中粒子的随机运动。这由随机微分方程控制:

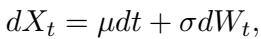
Equation for Brownian Motion

这里，\(dW_t\) 代表随机“噪声”或增量。转换规则是一个高斯 (正态) 分布。

LLM 能够完美地重构这种高斯形状。

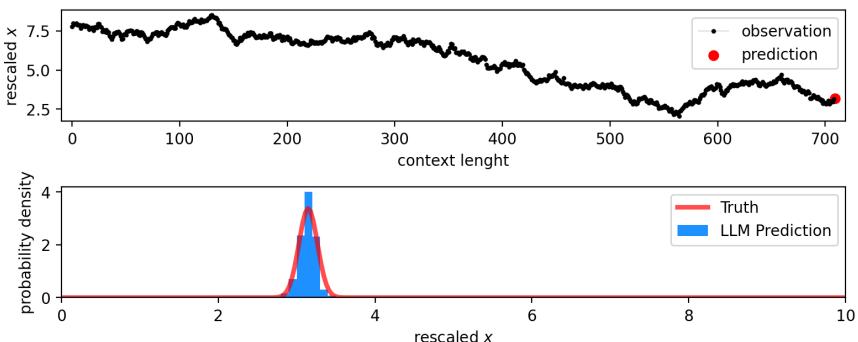
Figure 10: Next state prediction of Brownian motion.

在 图 10 中，红线是基本真值 (钟形曲线) 。蓝色直方图是 LLM 的预测。模型不仅猜出了均值 (中心) ，而且正确估计了噪声的 方差 (宽度) 。

案例 3: 混沌系统 (Logistic 映射)

也许最困难的测试是混沌。混沌系统是确定性的 (没有随机性) ，但极其敏感。起点的微小变化会导致截然不同的结果。

研究人员使用了 Logistic 映射 , 这是一个人口增长模型:

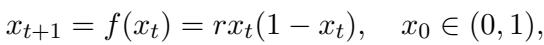
Equation for Logistic Map

当参数 \(r=3.9\) 时，该系统表现出混沌行为。

Figure 15: Next state prediction of the logistic map.

看 图 15 。 上图显示了混沌时间序列。下图显示了对最后一步的预测。

  • 真值 (红线) : 由于系统是确定性的，“真实”概率是在确切正确值上的一个尖峰 (狄拉克 \(\delta\) 函数) 。
  • 预测 (蓝条) : LLM 将几乎所有的概率质量都放在了那个确切值上。

仅仅通过观察序列，它就“解开”了方程。

学习混沌中的噪声

研究人员随后向 Logistic 映射添加噪声，使其变为随机的。现在模型必须预测一个方差不断变化的移动目标。

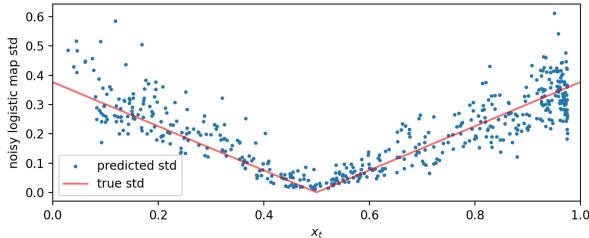
Figure 7: Noisy logistic map standard deviation as a function of the state value x_t.

图 7 (下图) 特别令人印象深刻。红线显示了系统的真实标准差 (波动率) ，它随当前值 \(x_t\) 的变化而变化。蓝点是 LLM 预测的标准差。模型学会了 不确定性不是恒定的——它随系统状态而变化。

发现: 上下文神经缩放定律

这篇论文最深刻的发现不仅仅是 LLM 可以学习这些系统，而是它们 如何 学习这些系统。

在深度学习中，我们熟悉“缩放定律”——经验法则表明“如果你将模型规模或数据规模增加一倍，损失会减少 X 量”。这些通常适用于 训练。

这篇论文提出了一个 上下文神经缩放定律 。 它描述了模型对物理规则的理解如何随着 提示 (上下文窗口) 长度的增加而提高。

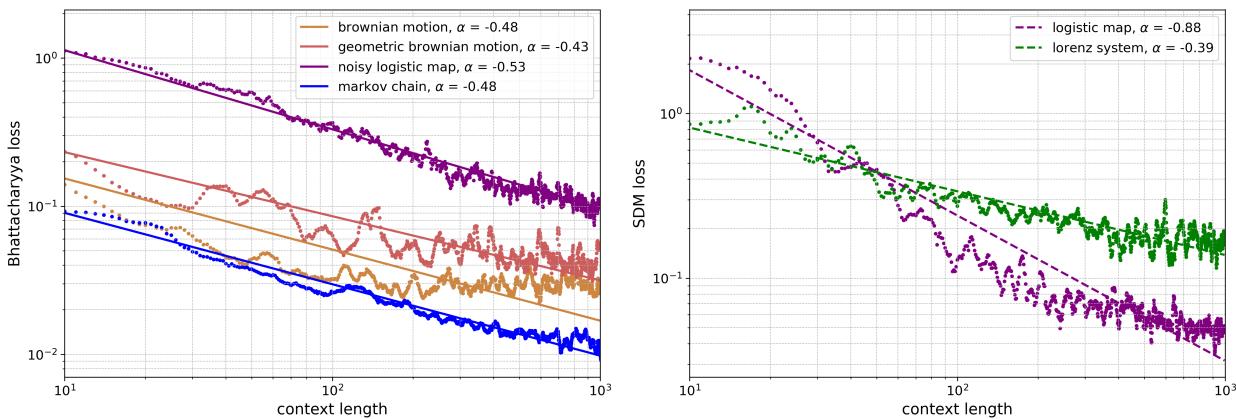
Figure 20: In-context loss curves from LLaMA-13b fitted with power law.

图 20 展示了这些幂律。

  • 左侧 (随机) : 双对数坐标图上的直线表明了幂律关系。对于“噪声 Logistic 映射” (紫色) ，随着上下文长度从 10 增加到 1,000，误差持续下降。
  • 右侧 (确定性) : Logistic 映射 (品红色) 显示出急剧下降。

支配这种行为的方程是:

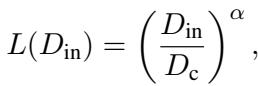
Equation for In-Context Scaling Law

其中 \(D_{in}\) 是上下文长度，\(\alpha\) 是缩放指数。这表明 LLM 在内部执行一种数据驱动的算法，类似于统计学家在收集更多样本时更新置信区间的方式。

讨论: 这只是死记硬背吗？

怀疑论者可能会问: “LLM 是真的在学习物理，还是只是在匹配它在海量训练数据中看到的模式？”

为了测试这一点，作者将 LLM 与标准基线进行了比较:

  1. Unigram/Bigram 模型: 简单的统计计数器。
  2. AR1 (自回归) 模型: 标准时间序列工具。
  3. 神经网络: 一个专门针对该序列实时训练的小型神经网络。

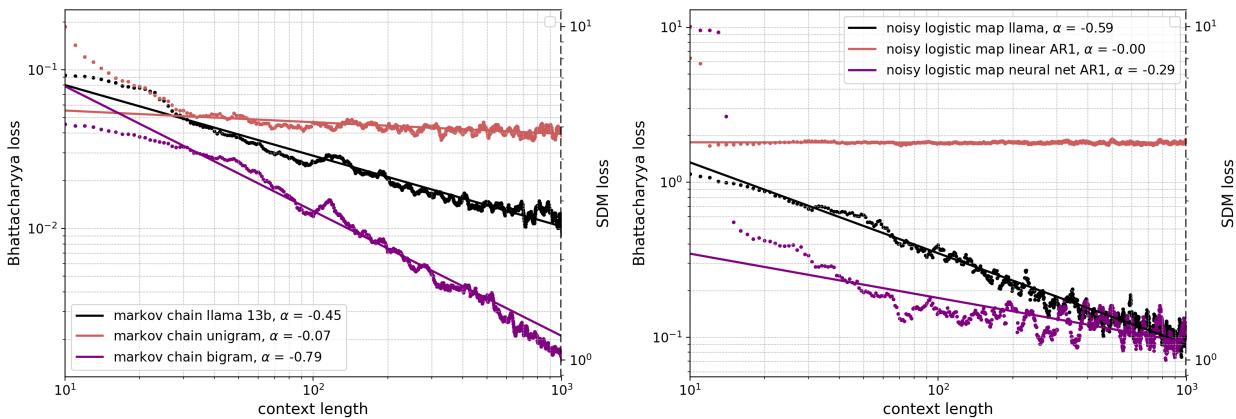
Figure 21: LLM in-context loss curves against the baseline model loss curves.

图 21 显示了比较结果。

  • 左侧 (马尔可夫链) : LLaMA 模型 (黑色) 的表现与 Bigram 模型 (紫色) 相当，后者是该任务的理论理想模型。
  • 右侧 (噪声 Logistic 映射) : LLaMA 模型击败了线性 AR1 基线 (红色) ，并与现场训练的专用神经网络 (紫色) 表现相当。

这表明 LLM 正在实施一种 上下文 学习算法，其效果与使用梯度下降从头开始训练专用神经网络一样有效。

结论与启示

这项研究架起了自然语言处理与科学建模之间的桥梁。它证明了大型语言模型不仅仅是重复文本的“随机鹦鹉”；它们是通用的模式识别引擎，能够推断复杂的数学规则。

主要结论如下:

  1. 零样本物理: LLM 无需微调即可模拟随机、混沌和连续系统。
  2. Hierarchy-PDF: 我们可以从 LLM 中提取精确的、多分辨率的概率分布，使其能够充当模拟器。
  3. 上下文缩放: 习得物理规律的准确性随上下文长度呈幂律缩放，表现得像一个正统的统计学习算法。

这为使用 LLM 分析潜在方程未知的实验数据打开了大门。也许有一天，我们不再需要手动推导模型，只需将数据输入 LLM，让它来描述宇宙的定律。