如果你玩过像 GPT-4 或 Llama 这样的大语言模型 (LLM) ，你应该非常熟悉它们遵循模式的能力。你只需提供几个例子——比如一串后面跟着表情符号的电影标题——模型就能领会其中的“氛围”，生成完美符合该模式的新例子。这种现象通常被归类为上下文学习 (In-Context Learning, ICL) 。

但这其中有一个经常被忽视的细微差别。LLM 不仅仅是在进行分类 (学习标签) ；它们还能生成复杂的、结构化的序列，以延续你在提示词中定义的特定“主题”或格式。这篇论文 “On the In-context Generation of Language Models” 背后的研究人员将这种能力称为上下文生成 (In-Context Generation, ICG) 。

谜题不仅在于 LLM 能做到这一点，真正的难题在于，它们能够针对在训练过程中从未明确重复过的 “主题”或模式做到这一点。一个在静态互联网文本上训练的模型，是如何仅仅通过看几个例子，就学会动态适应一个奇怪的数学谜题或自定义代码格式的呢？

在这篇文章中，我们将深入探讨这篇论文。我们将探索一个将 ICG 视为“下一个主题预测”问题的理论框架，研究一个模拟人类写作方式的巧妙潜变量模型 (Latent Variable Model) ，并分析基于合成数据的实验，这些实验揭示了究竟是什么让这种“涌现”能力成为可能。

三种类型的主题

要理解 ICG，首先需要对模型实际生成的内容进行分类。直觉上，我们要么认为 LLM 擅长 ICG 是因为它们在训练数据中见过类似的列表 (比如包含无数影评的 IMDB 页面) 。这被称为重复模式 (Repetition Mode) 。

然而，研究人员将主题分为三个截然不同的类别，以测试 LLM 的极限:

  1. 重复主题 (Repeated Topics) : 在预训练数据中频繁出现并连续重复的内容 (例如论坛上的电影评论) 。
  2. 非重复主题 (Nonrepeated Topics) : 在训练数据中出现过，但通常独立存在、没有重复的内容 (例如特定的 Python 类方法定义) 。
  3. 未见主题 (Unseen Topics) : 理论上从未在训练数据中出现过的内容 (例如“不自然的加法”，如 1-1=2) 。

如下图所示，Llama2-13B 可以处理所有这三种类型。它可以生成影评 (重复主题) 、复杂的代码结构 (非重复主题) ，甚至是奇怪的逻辑谜题 (未见主题) 。

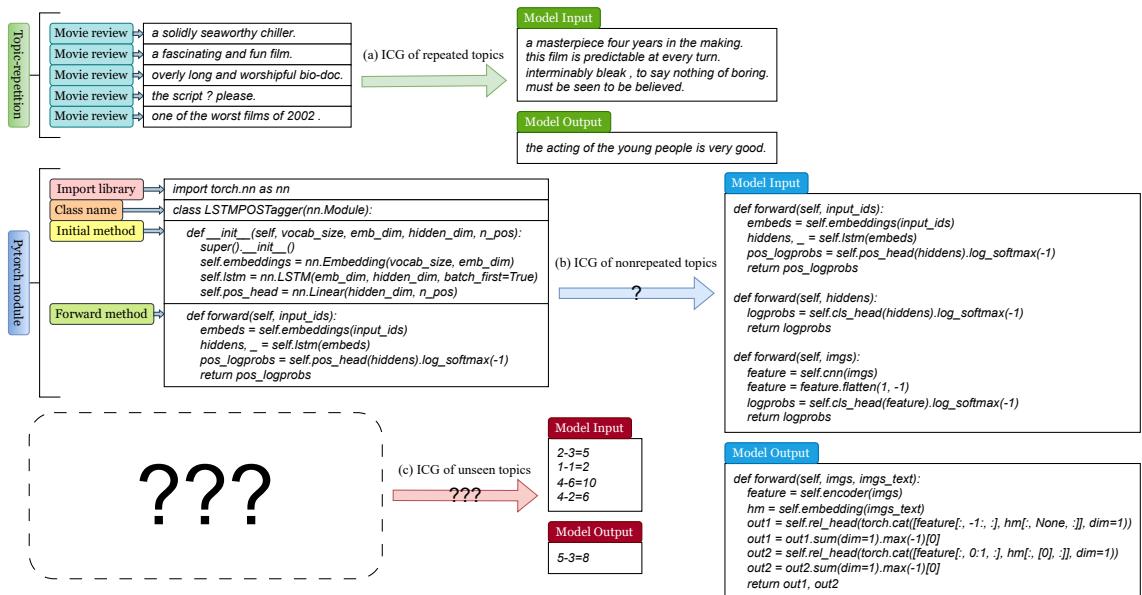
图 1: 不同类型主题的 ICG 示例 (由 Llama2-13B 生成) 。

处理第二类和第三类主题的能力正是作者所称的 ICG 泛化 (ICG-generalization) 。 模型不仅仅是在背诵记忆的模式；它正在将“重复”这一概念泛化到新的、陌生的领域。

对预训练分布进行建模

为了科学地研究这一点，我们不能依赖混乱的开放互联网数据。我们需要一个受控环境。作者提出了一个分层潜变量模型 (Hierarchical Latent Variable Model, LVM) 来从数学上描述文档是如何生成的。

可以将这个模型看作是对人类作家的模拟。在撰写文档时，人类遵循一系列决策层级:

  1. 模式 (\(\alpha\)): 决定体裁 (例如，“叙事”、“信件”或“重复”) 。
  2. 大纲 (\(\beta_{1:N}\)): 根据模式规划段落的结构或主题。
  3. 段落 (\(x_i\)): 根据选定的主题撰写实际文本。

研究人员将这一过程可视化为一个贝叶斯网络:

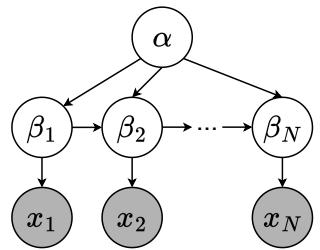
图 2: 预训练分布的贝叶斯网络，其中非阴影节点为潜变量。

这种结构允许我们将“主题转移” (故事如何发展) 与“生成” (实际的文字) 解耦 。 该模型的联合分布定义为:

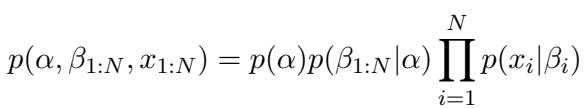
联合分布公式

重复假设

这一理论的核心依赖于对训练数据的一个特定假设。作者假设存在一种特定的模式，称为重复模式 (Repetition Mode, \(\hat{\alpha}\)) 。 当作者 (或生成过程) 处于这种模式时，大纲规定主题必须重复。

从数学上讲，如果你处于重复模式，下一个主题与当前主题相同的概率为 1。

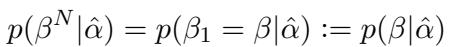
公式: 给定重复模式下 beta 的概率

这个简单的假设为 ICG 提供了理论锚点。如果模型能根据提示词推断出它当前处于“重复模式”，它就知道下一个主题必须与前几个相同。

将 ICG 形式化为下一个主题预测

有了这个模型，我们可以正式定义上下文生成到底是什么。它不是魔法；它是概率推理。

该假设认为，当给 LLM 一个提示词 \(x_{1:N}\) (一连串例子) 时，它会隐式地尝试预测潜在的主题 \(\hat{\beta}\)。如果模型工作正常，它为下一个输出选择相同主题 \(\hat{\beta}\) 的概率应该接近 1。

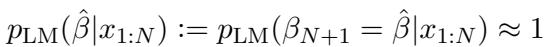
公式: LLM 选择 beta 的概率

相应地，生成文本的分布应该与该主题的真实分布相匹配:

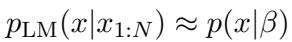
公式: LLM 生成文本分布

数学保证

论文提供了一个严格的数学证明 (定理 1) ，指出如果 LLM 很好地拟合了预训练分布，那么对于重复主题 , ICG 在理论上是有保证的。

该逻辑遵循贝叶斯推断 。 随着提示词中重复示例数量 (\(N\)) 的增加，模型越来越确定它处于“重复模式”。

当 \(N\) 趋于无穷大时，主题预测概率的极限为 1:

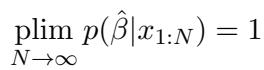
公式: N 趋于无穷大时主题概率的极限

这意味着生成的输出分布将收敛于真实的主题分布:

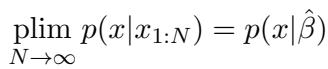
公式: 生成输出分布的极限

理想情况下，计算涉及对所有可能的主题和模式求和。下一个主题的概率是所有模式的混合:

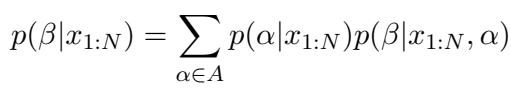
公式: 按模式分解的 beta 概率

然而，由于提示词在重复相同的主题，“重复模式”在计算中占据主导地位。复杂的混合坍缩为一个由重复模式 \(\hat{\alpha}\) 主导的简单后验分布:

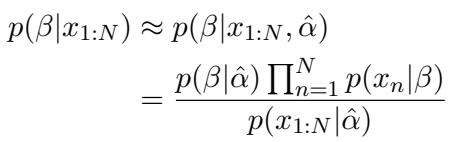
公式: 给定重复模式下 beta 的近似值

这证实了对于模型在训练期间见过重复的主题，ICG 是最小化困惑度 (perplexity) 的自然结果。模型看到重复，推断出“我应该重复”，然后生成已习得的主题。

泛化难题

上述理论解释了为什么 LLM 可以延续一系列影评 (重复主题) 。但它并不能解释为什么它们可以延续一系列“不自然的加法”算式 (未见主题) 。如果一个主题从未在训练数据中重复出现过，其重复的先验概率为零。贝叶斯更新应该会失败。

然而，LLM 确实能够泛化。为了理解原因，研究人员从理论转向了使用合成数据的实证实验。

设计合成世界

他们创建了一个受控的合成数据集，在其中可以操纵“语言”的属性。

  • 词汇表: 324 个 token。
  • 结构: 文档由 30 个段落组成。
  • 组合性 (Compositionality) : 这是关键。他们定义的“主题”不是原子单位，而是子主题 (或子结构) 的组合。

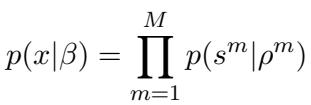
公式: 段落概率作为子主题的乘积

在这种设置中，一个“主题”是 \(M\) 个子主题的元组。即使某个特定的组合 (主题) 是未见过的，它的组成部分 (子主题) 可能在其他上下文中出现过。这模仿了自然语言，即新句子是已知单词和语法结构的全新组合。

下面是合成数据集的可视化。你可以看到不同的模式 (连续模式 vs. 重复模式) 以及主题是如何构成的。

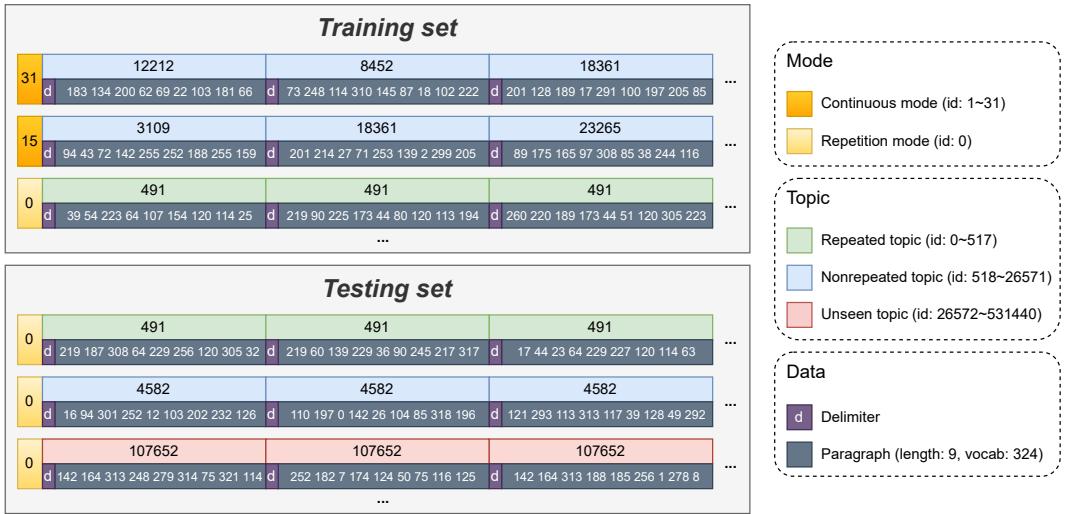
图 3: 合成数据集中的示例，其中我们设置 M=3, r_R=1/1024 且 gamma=0.01。

实验结果: 什么驱动了泛化？

研究人员在这个合成数据上训练了不同大小的 Transformer 模型 (从 21 亿到 39 亿个 token 不等) 。他们改变了组合元数 (Composition Arity, \(M\)) (构成一个主题的子部分数量) 和训练数据中重复主题的比例 (\(r_R\)) 。

他们使用 ICTR (上下文主题重复率，In-Context Topic-Repetition) 来衡量性能，这本质上是追踪模型成功保持主题的频率。

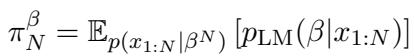
公式: ICTR 的定义

他们将此指标细分为重复 (\(R\)) 、非重复 (\(C\)) 和未见 (\(U\)) 主题。

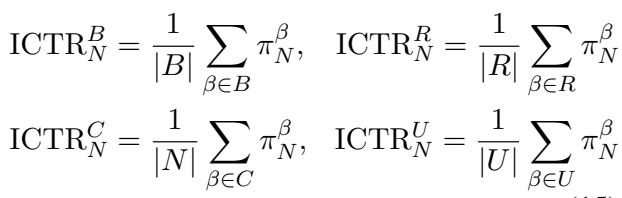
公式: 按主题类型细分的 ICTR

关键发现 1: 组合性为王

ICG 泛化最重要的单一因素是数据的组合性。

看下面的热力图 (图 4a) 。

  • M=2 (低组合性) : 即使是大模型也难以泛化。它们可以学会重复训练期间见过的重复主题 (Repeated topics) ，但在未见主题上会失败。
  • M=3 & M=4 (高组合性) : 突然间，泛化出现了。即使训练数据中重复主题的比例非常小，模型也能在未见主题 (绿色单元格) 上执行 ICG。

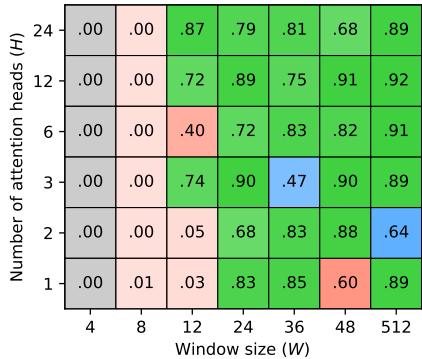
图 4: ICG 泛化结果，模型状态热力图。

这表明 LLM 通过识别提示词中熟悉的“子结构”来处理新任务。如果数据具有足够的组合性，模型就能学会将这些已知的子结构重组为新的模式。

关键发现 2: “顿悟”阈值

存在一个明显的相变。模型不是逐渐学会泛化的；它是突然掌握的。随着训练数据中重复主题比例 (\(r_R\)) 的增加，模型从欠拟合 (Underfit) -> 过拟合 (Overfit) (仅记忆重复主题) -> 泛化 (Generalization) (处理未见主题) 。

较大的模型 (如 \(X^2L\)) 比小模型 (如 \(X^2S\)) 更快达到这个泛化阈值。

关键发现 3: 大小很关键，头数不重要

研究人员分析了 Transformer 架构本身。

  • 窗口大小 (\(W\)) : 大的注意力窗口至关重要。如果模型不能回看足够远的距离来观察重复历史，它就无法推断出模式。
  • 模型深度/宽度: 较大的模型在泛化方面明显更好。
  • 注意力头数 (\(H\)) : 令人惊讶的是，注意力头的数量并不非常重要。如下表 (图 4c) 所示，只要模型在其他方面有足够的容量，减少头的数量 (甚至降到 1 或 2 个) 几乎不会影响泛化能力。

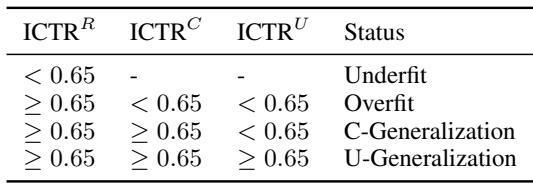
展示注意力头数和窗口大小影响的表格。

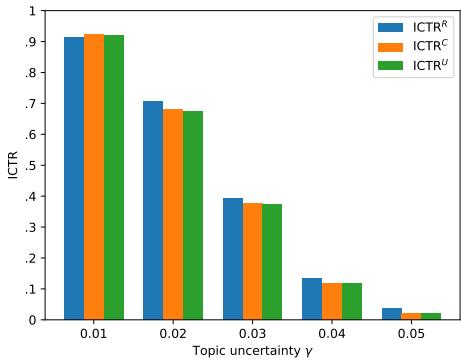
关键发现 4: 主题不确定性

他们还测试了“主题不确定性” (\(\gamma\)) ，它控制不同主题之间的区分度。有趣的是，这会影响拟合数据的整体难度 (学习有多难) ，但并不会真正改变重复主题和未见主题之间的差距。如果模型学会了一个，它也就学会了另一个。

图 5: 模型 L 在不同主题不确定性下不同主题的 ICTR。

收敛速度

最后，研究人员查看了提示词中需要多少个例子 (Shots) ，模型才能识别出模式。

  • 较大的模型通常收敛得更快 (需要更少的样本) 即可达到高准确率。
  • 较大的窗口尺寸允许性能在更高的准确率水平上趋于平稳。

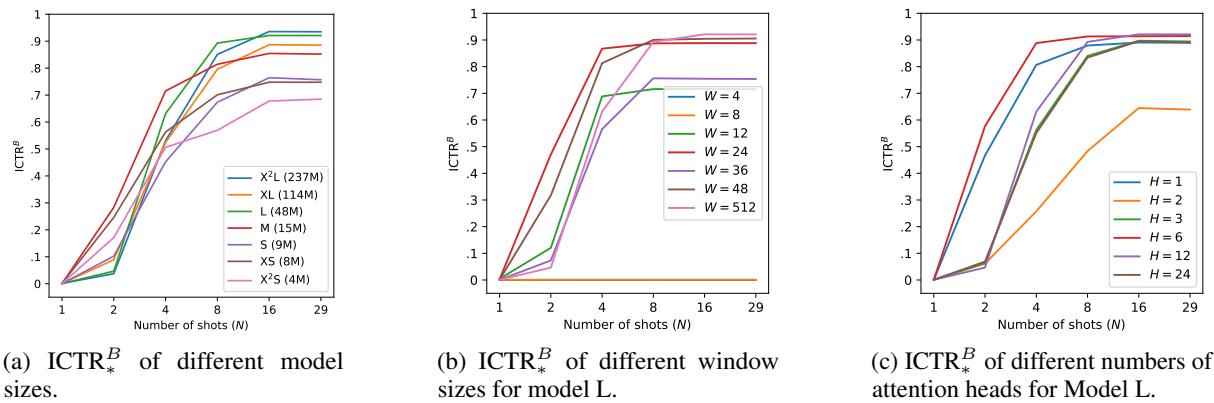
图 6: 不同模型配置的 ICTR 与样本数量的关系。

结论

这篇论文揭开了 LLM 最神奇能力之一的神秘面纱。上下文生成并不是机器中涌现出的神秘灵魂；它是概率和数据结构的可以预测的结果。

  1. 训练中的重复: 重复数据的存在 (如论坛或代码库) 教会了模型“重复模式”。
  2. 贝叶斯推断: 在推理过程中，模型看到重复的提示词，识别出“重复模式”，并预测下一个主题必须与之前的相匹配。
  3. 用于泛化的组合性: 将此逻辑应用于新主题的能力来自于语言是具有组合性的这一事实。模型识别出熟悉的子组件 (语法、逻辑、代码句法) ，并将重复规则应用于这些在预训练期间获得的“乐高积木”，即使具体的组合是全新的。

这解释了为什么像 GPT-4 这样的模型如此通用。它们不仅仅是在背诵段落；它们正在学习“重复模式”这一抽象规则，并将其应用于语言的构建块上。